-
https://leetcode.cn/problems/word-break-ii
-
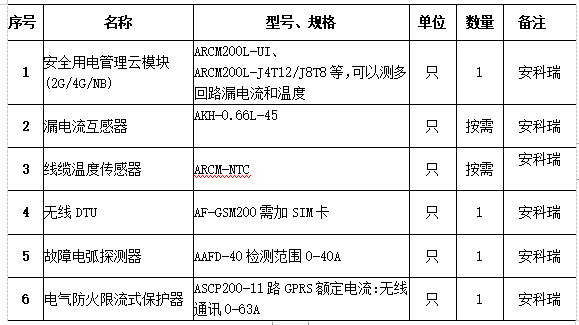
给定一个字符串 s 和一个字符串字典 wordDict ,在字符串 s 中增加空格来构建一个句子,使得句子中所有的单词都在词典中。以任意顺序 返回所有这些可能的句子。
-
注意:词典中的同一个单词可能在分段中被重复使用多次。
示例 1:
输入:s = "catsanddog", wordDict = ["cat","cats","and","sand","dog"]
输出:["cats and dog","cat sand dog"]
示例 2:
输入:s = "pineapplepenapple", wordDict = ["apple","pen","applepen","pine","pineapple"]
输出:["pine apple pen apple","pineapple pen apple","pine applepen apple"]
解释: 注意你可以重复使用字典中的单词。
示例 3:
输入:s = "catsandog", wordDict = ["cats","dog","sand","and","cat"]
输出:[]
提示:
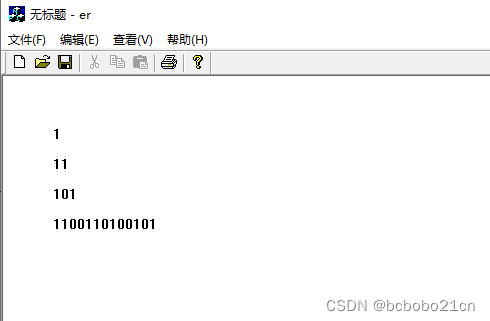
1 <= s.length <= 20
1 <= wordDict.length <= 1000
1 <= wordDict[i].length <= 10
s 和 wordDict[i] 仅有小写英文字母组成
wordDict 中所有字符串都 不同
题解
-
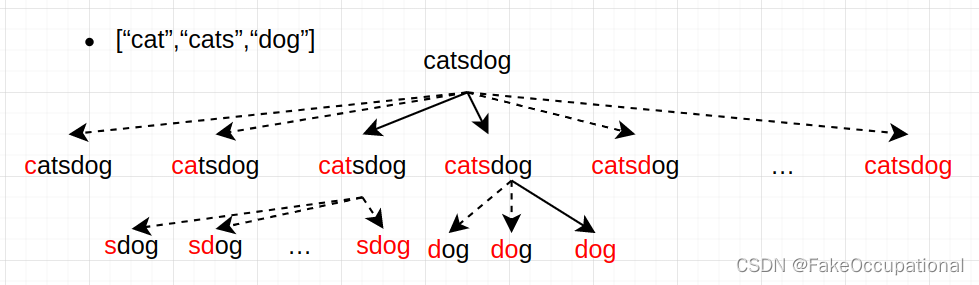
DFS解法:Input : 索引 Output:vector 或者 vector<vector >
-
记忆化DFS用于处理在其他分支遇到相同情况的
-
有重复部分的情况(dog部分)

-
没有重复部分的情况
-
记忆化DFS是一种优化搜索算法的方法,它通过在搜索过程中保存已经计算过的结果,避免重复计算,从而提高搜索效率。
具体来说,记忆化DFS的实现过程如下:
-
定义一个数组或哈希表,用于保存已经计算过的结果。数组或哈希表的下标是问题的状态,值是已经计算过的结果。
-
在DFS搜索过程中,首先检查当前状态是否已经计算过。如果已经计算过,直接返回保存的结果;如果没有计算过,继续进行搜索,并保存搜索结果。
-
在递归返回的过程中,将搜索结果保存到数组或哈希表中。
-
最后返回搜索结果。
记忆化DFS可以用于解决许多具有重叠子问题的问题,如动态规划、图论等问题。它可以大大减少重复计算,提高算法效率,但需要额外的空间来存储计算结果。
class Solution {
private:
unordered_map<int, vector<string>> ans;
unordered_set<string> wordSet;
public:
vector<string> wordBreak(string s, vector<string>& wordDict) {
wordSet = unordered_set(wordDict.begin(), wordDict.end());
backtrack(s, 0);
return ans[0];
}
void backtrack(const string& s, int index) {
if (!ans.count(index)) {// 返回与 key 比较等于指定参数的元素数,该参数为 1 或 0,因为此容器不允许重复
if (index == s.size()) {
ans[index] = {""};
return;
}
ans[index] = {};
for (int i = index + 1; i <= s.size(); ++i) {
string word = s.substr(index, i - index);
if (wordSet.count(word)) {
backtrack(s, i);
for (const string& succ: ans[i]) {// std::string str = std::string("hello") + " world"; 原因是在C++中,""括起来的字符串被当成是const char*类型,而非string类型。这是+操作无效
ans[index].push_back(succ.empty() ? word : word + " " + succ);
}
}
}
}
}
};