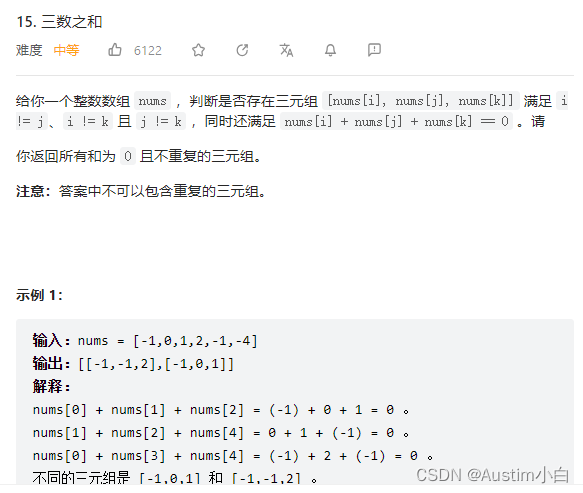
题目描述

*1.关于参数 int returnSize, int ** returnColumnSizes的理解
具体看这篇文章
[https://blog.csdn.net/m0_52775920/article/details/121461911?spm=1001.2014.3001.5502]
（1）*returnSize 的理解
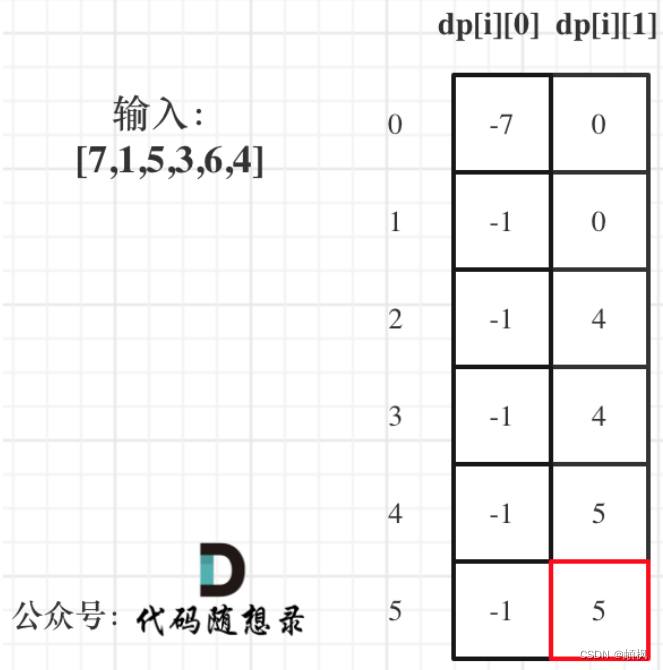
returnSize 返回大小为returnSize的二维数组，可以理解为returnSize就是一个指针，*returnSize就代表返回大小了，这里的大小就是我们要返回的二维数组的行数，比如上面图就是
（2）**returnColumnSizes的理解
*returnColumnSizes 是用来装我们返回的二维数组每一行有多少个元素的（即列数），如果返回 5 行，则 *returnColumnSizes 的长度也得是 5 ， 比如说第一个元素是 3 表示二维数组的第一行有 3 个数，第二个元素是 4 表示二维数组的第二行有 4 个数。别人怎么知道你的二维数组有多少行？自然也就不知道应该初始化 *returnColumnSizes 数组为多大了，这一切还得你来。你 malloc 一个数组，自然就会得到一个指向数组的一阶指针，

2.题目分析
给你一个包含 n 个整数的数组 nums，判断 nums 中是否存在三个元素 a，b，c ，使得 a + b + c = 0 ？请你找出所有和为 0 且不重复的三元组。注意：答案中不可以包含重复的三元组。利用双指针，a=nums[i] ,b= nums[left],c=nums[right]; 题目要求去重，即对abc去重；

# define MAX 100000	// 答案的个数，当然也能用动态扩容
int comp(const void *a, const void *b)
{
    return *(int *)a > *(int *)b ? 1 : 0;
}
int** threeSum(int* nums, int numsSize, int* returnSize, int** returnColumnSizes){
    qsort(nums, numsSize, sizeof(int), comp);
    int **ans = (int **)malloc(sizeof(int *) * MAX);
    *returnSize = 0;
    if (numsSize < 3)   return ans;
    int i = 0;
    while (i < numsSize - 2) {
        int left = i + 1, right = numsSize - 1;
        while (left < right) {
            int sum = nums[left] + nums[right] + nums[i];
            if (sum == 0) {
                int *temp = (int *)malloc(sizeof(int) * 3);
                temp[0] = nums[i];
                temp[1] = nums[left];
                temp[2] = nums[right];
                ans[(*returnSize)++] = temp;
            }
            // 这个地方不能是else if，因为总得改变当前的状态，如果是else if，那么找到了一个答案之后就永远不变了，这是不行的
            if (sum < 0)
                // 小了，就改变left。跳过重复的同时避免出界
                while (left < numsSize - 1 && nums[left] == nums[++left]);
            else
                // right跳过重复的
                while (right > 0 && nums[right] == nums[--right]);
        }
        // 第一个数字i，同样避免重复和越界
        while(i < numsSize - 1 && nums[i] == nums[++i]);
    }
    *returnColumnSizes = (int *)malloc(sizeof(int) * (*returnSize));
    for (int i = 0; i < (*returnSize); i++)
        (*returnColumnSizes)[i] = 3;
    return ans;
}

解法二：
1、判断输入数组为空、或元素个数小于3个，直接返回NULL
2、将输入数组升序排序
3、依次遍历排序后的数组
3.1、判断当前元素是否为正，是则结束循环，因为后续的数字也都为正，不会出现三数之和为0的情况
3.2、判断当前元素是否与上一次相等，相等则跳过进行去重
3.3、从 i + 1 到 numsSize - 1 进行左右指针判断三数之和sum：
3.3.1、sum == 0 ：
1、找到一组值，进行保存
2、对left、right进行去重
3.3.2、sum < 0 :
left++
3.3.3、sum > 0
right–

int cmp(const void* a, const void* b) {
    return *(int*)a - *(int*)b;
}
int** threeSum(int* nums, int numsSize, int* returnSize, int** returnColumnSizes){
    /* 先记录返回的行数为0 */
    *returnSize = 0;
    /* 输入为空、或元素个数小于3则返回NULL */
    if (nums == NULL || numsSize < 3) {
        return NULL;
    }
    /* 将nums排序为升序排列 */
    qsort(nums, numsSize, sizeof(int), cmp);
    /* 分配返回数组、返回数组的列数 */
    int** ret = (int**)malloc(numsSize * numsSize * sizeof(int*));
    *returnColumnSizes = (int*)malloc(numsSize * numsSize *sizeof(int));
    /* 排序后的数组从头到尾进行遍历 */
    for (int i = 0; i < numsSize; i++) {
        /* 当前数组大于0，表示后续没有三数之和为0，结束遍历 */
        if (nums[i] > 0) {
            break;
        }
        /* 当前元素与上一次相等，跳过此次计算，去重 */
        if (i > 0 && nums[i] == nums[i - 1]) {
            continue;
        }
        /* 定义左右指针 */
        int left = i + 1, right = numsSize - 1;
        /* 开始查找三数之和为0 */
        while (left < right) {
            int sum = nums[i] + nums[left] + nums[right];
            if (sum == 0) {
                ret[*returnSize] = (int*)malloc(sizeof(int) * 3);
                ret[*returnSize][0] = nums[i];
                ret[*returnSize][1] = nums[left];
                ret[*returnSize][2] = nums[right];
                /* 返回数组当前行的列数为3 */
                (*returnColumnSizes)[*returnSize] = 3;
                /* 返回数组的行数自加1 */
                (*returnSize)++;
                /* 对左右指针进行去重 */
                while (left < right && nums[left]  == nums[++left]);
                while (left < right && nums[right] == nums[--right]);
            } else if (sum < 0) {
                left++;
            } else {
                right--;
            }
        }
    }
    return ret;
}