1.简述
一、常见分布的随机数的产生
随机数是专门的随机试验的结果。在统计学的不同技术中需要使用随机数,比如在从统计总体中抽取有代表性的样本的时候。而matlab直接提供了产生随机数的通用函数,但针对不同的分布,函数形式会有所不同,但通用公式如下:
命令:namernd(A,B,m,n)
y = random(‘name’,A1,A2,A3, m, n)
说明:对于namernd(A,B,m,n)函数,m和n表示产生随机数的矩阵大小,例如m=1,n=1就表示产生一个随机数;m=2,n=2就表示产生一个2*2的随机数矩阵,name表示函数名。
下面表格列出了各种分布的随机数生成函数
函数名 调用形式 注 释
betarnd betarnd(A, B,m,n) 参数为A, B的β分布随机数
binornd binornd(N,P,m,n) 参数为N, p的二项分布随机数
chi2rnd chi2rnd(N, m, n) 自由度为N的χ 2 分布随机数
exprnd exprnd(Lambda,m,n) 参数为Lambda的指数分布随机数
frnd frnd(N1, N2, m,n) 第一自由度为N1,第二自由度为N2的F分布随机数
gamrnd gamrnd(A, B, m,n) 参数为A, B的γ分布随机数
geornd geornd(P,m,n) 参数为 P的几何分布随机数
hygernd hygernd(M,K,N,m,n) 参数为 M,K,N的超几何分布随机数
lognrnd lognrnd(MU, SIGMA, m, n) 参数为MU, SIGMA的对数正态分布随机数
nbinrnd nbinrnd(R, P,m,n) 参数为R, P的负二项式分布随机数
ncfrnd ncfrnd(N1, N2, delta,m,n) 参数为N1,N2, delta的非中心F分布随机数
nctrnd nctrnd(N, delta, m,n) 参数为N, delta的非中心t分布随机数
ncx2rnd ncx2rnd(N, delta, m,n) 参数为N, delta的非中心卡方分布随机数
normrnd normrnd(MU, SIGMA, m,n) 参数为MU, SIGMA的正态分布随机数
poissrnd poissrnd(Lambda,m,n) 参数为Lambda的泊松分布随机数
raylrnd raylrnd(B, m,n) 参数为B的瑞利分布随机数
trnd trnd(N, m,n) 自由度为N的t分布随机数
unidrnd unidrnd(N,m, n) 离散型均匀分布随机数
unifrnd unifrnd ( A,B,m,n) (A,B)上连续型均匀分布随机数
weibrnd weibrnd(A, B,m, n) 参数为A, B的威布尔分布随机数
2.代码及运行结果
%% 二项分布随机数的产生
clear all;
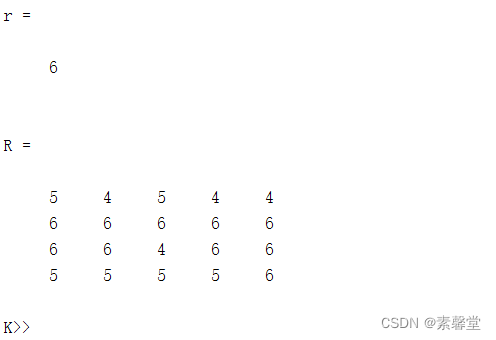
r=binornd(6,0.8)
R=binornd(6,0.8,4,5) %产生一个4*5的矩阵
%% 泊松分布
clear all;
r=poissrnd(6) %泊松分布
R=poissrnd(6,3,3) %产生一个3*3的矩阵
%%

% 指数分布
clear all;
r=exprnd(5) %指数分布
R=exprnd(5,5,5) %产生一个5*5的矩阵
%%
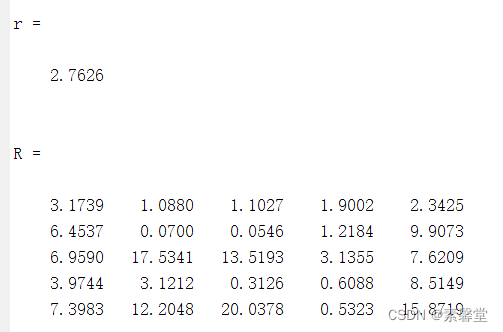
% 均匀分布 连续型
clear all;
r=unifrnd(1,5) %均匀分布 1到5之间
R1=unifrnd(1,5,3,3) %产生一个3*3的矩阵
R2=unifrnd(1,5,[3 3])
%%


% 离散型均匀分布
clear all;
r=unidrnd(6) %离散型均匀分布
R1=unidrnd(6,3,3) %产生一个3*3的矩阵
R2=unidrnd(6,[3 3])

%% 正态分布 应用最广 非常重要
clear all;
r=normrnd(0,1)
R1=normrnd(0,1,[3 4]) %产生一个3*4的矩阵 均值为0 标准差为1
R2=normrnd(2,4,[3 4])