01-线性表 (数据结构和算法)

要点：

程序 = 数据结构 + 算法

一、数据结构的概述

程序 = 数据结构 + 算法

数据结构：计算机存储、组织数据的方式

算法：处理数据的方式

1.1 基本概念和术语

1、数据

数据（data）：所有能够输入到计算机中去的描述客观事物的符号。

数值型数据：表示数量，由数字、小数点、正负号和表示乘幂的字母E组成。数值型的数据是不能包含文本的，必须是数值
非数值型数据：如文字、图像、声音等的计算机应用领域

2、数据元素

数据元素（data element）：数据的基本单位，也称之为结点（node）或者记录（record）

3、数据对象

数据对象（data object）：相同特性数据元素的集合，是数据的一个子集。

整型数据对象：所有正负整数的集合，其中的每一个整数就是一个数据元素

1.2 数据结构的分类

传统上，我们可以把数据结构分为逻辑结构和物理结构两大类：

逻辑结构分类：逻辑结构是从具体问题中抽象出来的模型，是抽象意义上的结构，按照对象中数据元素之间的相互关系分类，也是我们后面课题中需要关注和讨论的问题
- 集合结构：集合结构中数据元素除了属于同一个集合外，他们之间没有任何其他的关系
- 线性结构：线性结构中的数据元素之间存在一对一的关系
- 树形结构：树形结构中的数据元素之间存在一对多的层次关系
- 图形结构：图形结构的数据元素是多对多的关系
物理结构分类：逻辑结构在计算机中真正的表示方式（又称为映像）称为物理结构（实际存储结构），也可以叫做存储结构。常见的物理结构有顺序存储结构、链式存储结构。
- 顺序存储结构：把数据元素放到地址连续的存储单元里面，其数据间的逻辑关系和物理关系是一致的，比如我们常用的数组就是顺序存储结构。
- 链式存储结构：把数据元素存放在任意的存储单元里面，这组存储单元可以是连续的也可以是不连续的。此时，数据元素之间并不能反映元素间的逻辑关系，因此在链式存储结构中引进了一个指针存放数据元素的地址，这样通过地址就可以找到相关联数据元素的位置。

二、线性表

2.1 线性结构概述

1、线性表是一种典型的线性结构：则有且仅有一个开始结点和一个终端结点，并且所有结点都最多只有一个直接前趋和一个直接后继。

2、线性结构表达式：（a1, a2, a3, ...... , ai）

3、线性结构特点:

只有一个首结点和尾结点
除首尾结点外，其他结点只有一个直接前驱和一个直接后继

简言之，线性结构反映结点间的逻辑关系是一对一的。

4、线性结构包括线性表、堆栈、队列、字符串、数组等等。

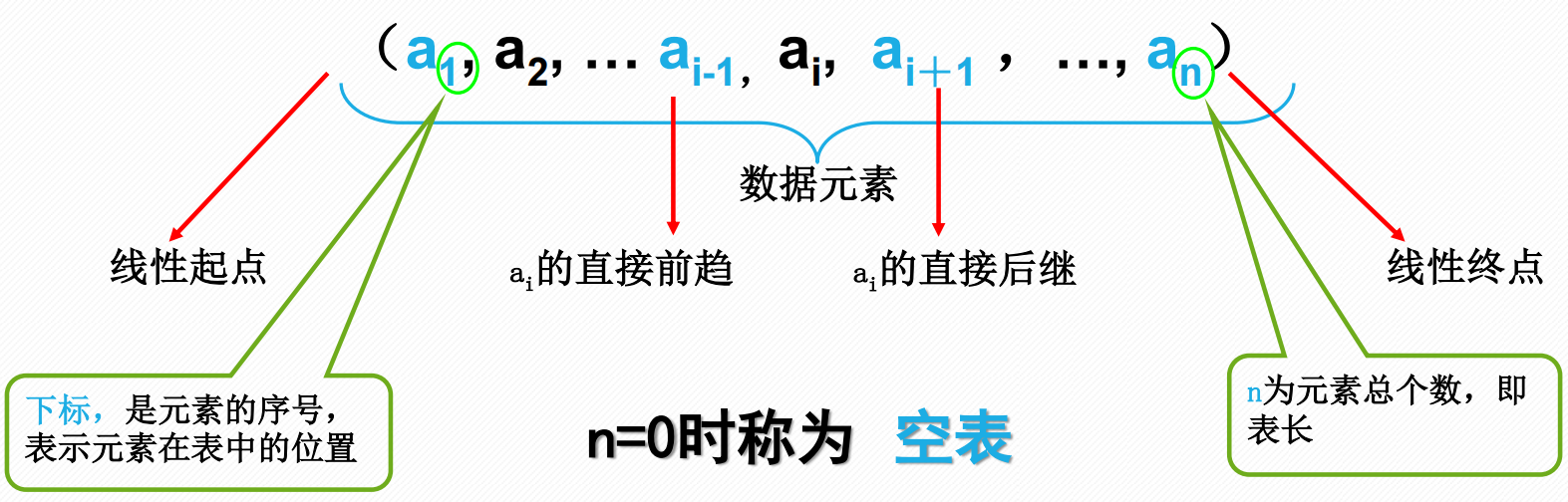
线性表是最基本、最简单、也是最常用的一种数据结构。一个线性表是n个具有相同特性的数据元素的有限序列。

如果把线性表用数学语言来定义，则可以表示为(a1,...ai-1,ai,ai+1,...an)，ai-1领先于ai,ai领先于ai+1，称ai-1是ai的前驱元素，ai+1是ai的后继元素。

线性表中数据存储的方式可以是顺序存储，也可以是链式存储，按照数据的存储方式不同，可以把线性表分为顺序表和链表。

线性表的基本操作：初始化、取值、查找、插入、删除。

顺序表是在计算机内存中以数组的形式保存的线性表，线性表的顺序存储是指用一组地址连续的存储单元，依次存储线性表中的各个元素。

typedef int ElemType;
typedef unsigned int uint;
typedef struct{
    ElemType *elem;  //顺序表中存储数据的空间
    uint length;     //当前存储数据的个数
    uint listSize;   //顺序表的容量，最多可以存储的元素的个数
}SqList;

2.2 初始化顺序表

逻辑：

为存储数据的指针分配空间
顺序表长度初始化为0
顺序表的容量为分配的空间 sizeof(ElemType)

/*
 * @brief  初始化顺序表
 * @param listSize 顺序表容量
 * @return 返回初始化好的顺序表
 * */
SqList SqList_init(uint listSize){
    //为线性表存储数据分配空间
    SqList t;
    t.elem = (ElemType *)malloc(listSize*sizeof(ElemType));
    t.length = 0;
    t.listSize = listSize;
    return t;
}

2.3 顺序表的输出

逻辑：

根据顺序表的长度遍历整个顺序表
将遍历到的每一个数据元素输出

/*
 * @brief 打印顺序表的所有的元素
 * @param t 需要输出的顺序表
 * @return void
 * */
void print_SqList(SqList t){
    printf("SqList print: ");
    int i;
    for (i = 0; i < t.length; i++){
        printf("SqList_data, %d", t.elem[i]);
    printf("\n");
    }
}

2.4 顺序表的取值

逻辑：

判断需要获取的元素下标是否合法
如果不合法则返回一个出错编号
如果合法直接返回下标所对应的元素

/*
 * @brief 获取顺序表中某个位置的元素
 * @param t 需要操作的顺序表
 * @param index 需要获取的元素的位置/下标
 * @return ElemType 获取到的元素
 * */
ElemType get_elem(SqList t, uint index){
    if (index >= t.length){
        printf("index out of range \n");
        return -1;
    }
    return t.elem[index];
}

2.5 顺序表元素的查找

逻辑：

通过顺序表的长度遍历整个顺序表
将遍历到的元素与需要查找的元素比较，如果不相等则继续往后遍历
如果相等则停止遍历，退出循环
返回遍历到的元素的下标

/* @brief 在顺序表中查找指定的元素
 * @param t 需要操作的顺序表
 * @param elem 需要查找的元素
 * @return int 成功返回值元素的下标，失败返回-1
 * */
int find_elem(SqList t, ElemType elem){
    int index = -1;  //保存元素的下标，默认需要查找的元素不在顺序表中
    //遍历整个顺序表
    int i;
    for (i = 0; i < t.length; i++){
        if (t.elem[i] == elem){
            index = i;
            break;
        }
    }
    
    if (-1 == index)
        printf("Can not find element : %d\n", elem);
    return index;
}

2.6 顺序表的销毁

逻辑：

释放初始化顺序表时在堆上分配的空间
将顺序表的长度设置为0
将顺序表的容量设置为0

/*
 * @brief 销毁一个顺序表
 * @param t 需要销毁的顺序表指针
 * */
int SqList_destroy(SqList *t){
    if (NULL == t)
        return error;
    if (t->elem != NULL){
        free(t -> elem);
        t->length = 0;
        t->listSize = 0;
    }
    return success;
}

2.7 删除指定位置的元素

逻辑：

判断需要删除的元素下标是否合法，如果不合法返回出错码
将第i+1至length-1（最后一个元素的下标）位的元素往前移动一个位置
顺序表长度 -1

/*
 * @brief 删除指定位置的元素
 * @param t 需要操作的顺序表指针
 * @param index 需要删除的元素的下标
 * */
int locate_elem_delete(SqList *t, uint index){
    if (NULL == t)
        return error;
    if (index >= t->length){
        printf("index out of range ...\n");
        return error;
    }
    int i;
    //删除第index个节点，后面的数据移动 t->length - (index + 1)次
    //将第index+1开始到第t.length-1位置的元素往前移动
    for (i=0; i < t->length - (index + 1); i++){
        t->elem[index+i] = t->elem[index+i+1];
    }
    t->length--;
    return success;
}

2.8 删除指定的元素

逻辑：

遍历整个顺序表
判断遍历到得元素是否为需要删除得元素，如果不是则继续往后遍历
如果相等则将该元素后面得所有元素往前移动一个位置

/*
 * @brief 将顺序表中指定的元素删除
 * @param t 需要操作的顺序表指针
 * @param elem 需要删除的元素
 * @return 成功返回OK，失败返回error
 * */
int delete_designated_elem(SqList *t, ElemType elem){
    if (NULL == t){
        printf("[%s %d] SqList is NULL\n", __FUNCTION__ , __LINE__);
        return error;
    }
    
    int i = 0;
    while (i != t->length){
        //先找到需要删除的元素
        if (t->elem[i] != elem){
            i++;
            continue;
        }
        //记录其位置
        int p = i;
        int j;
        //将后面的元素往前移动一个位置
        for (j = 0; j < t->length - (p + 1); j++){
            //将第index + i + 1个元素 覆盖掉第 index + i个元素
            t->elem[p + j] = t->elem[p + j + 1];
        }
        t->length--;
    }
    return success;
}

2.9 顺序表的扩容

逻辑：

将顺序表的容量扩大到原来的两倍

/*
 * @brief 为顺序表扩容
 * @param t 需要扩容的顺序表指针
 * @return 成功返回success， 失败返回error
 * */
int SqList_expand(SqList *t){
    if (NULL == t){
        printf("[%s %d] SqList is NULL \n", __FUNCTION__ , __LINE__);
        return error;
    }
    //为顺序表分配新的空间
    t->listSize *= 2;
    t->elem = (ElemType *)realloc(t->elem, t->listSize * sizeof(ElemType));
    return success;
}

2.10 在指定位置前插入元素

逻辑：

判断插入的位置是否合法
判断顺序表是否满了，如果满了则扩容
根据插入的位置计算需要移动的元素个数/次数
将指定位置开始的所有元素整体往后移动一个位置（从最后一个位置开始往后移动）
将需要插入的元素放置到插入的位置
顺序表长度+1

/*
 * @brief 在指定位置的前面插入一个元素
 * @param t 需要操作的顺序表指针
 * @param index 需要插入的位置
 * @param elem 需要插入的元素
 * @return error 成功返回success， 失败返回error
 * */
int elem_insert(SqList *t, uint index, ElemType elem){
    if (NULL == t){
        printf("[%s %d] SqList is NULL \n", __FUNCTION__ , __LINE__);
        return error;
    }
    //判断插入的位置是否合法
    if (index > t->length)
        return error;
    //判断顺序表是否满了，如果满了则扩容
    if (t->length == t->listSize){
        SqList_expand(t);
        print_SqList(*t);
    }
    int i;
    for (i = 0; i < t->length - index; i++){
        //从最后一个元素开始移动
        t->elem[t->length+i] = t->elem[t->length-1+i];
    }
    //将需要插入的元素放置到插入的位置
    t->elem[index] = elem;
    t->length++;
    return success;
}