目录
前言
快速排序
实现逻辑
1. hoare版本编辑
2. 挖坑法
3. 前后指针版本
快速排序优化
1. 三数取中法选key
2. 递归到小的子区间时,可以考虑使用插入排序
快速排序非递归(用栈实现)
快速排序的特性总结
全部代码
前言
🥰在学数据结构的第一节课就知道了数据结构课程是要管理并且学会操作数据,当然操作数据首先想到的就是数据的排序,排过顺序的数据的使用价值才够大。前面我们学习了顺序表也学习了链表等等,这些就是储存数据的方法,下面我们来看一看传说中的快速排序的特点与效率怎么样。😍
快速排序
快速排序,又称划分交换排序(partition-exchange sort)
| 中文名 | 快速排序算法 | 外文名 | quick sort |
| 别 名 | 快速排序 | 提出者 | C. A. R. Hoare |
| 提出时间 | 1960年 | 时间复杂度 | O ( |
| 空间复杂度 | O ( |
快速排序是Hoare于1962年提出的一种二叉树结构的交换排序方法,其基本思想为:任取待排序元素序列中的某元素作为基准值,按照该排序码将待排序集合分割成两子序列,左子序列中所有元素均小于基准值,右子序列中所有元素均大于基准值,然后最左右子序列重复该过程,直到所有元素都排列在相应位置上为止。
实现逻辑
快速排序使用分治法(Divide and conquer)策略来把一个序列(list)分为两个子序列(sub-lists)。
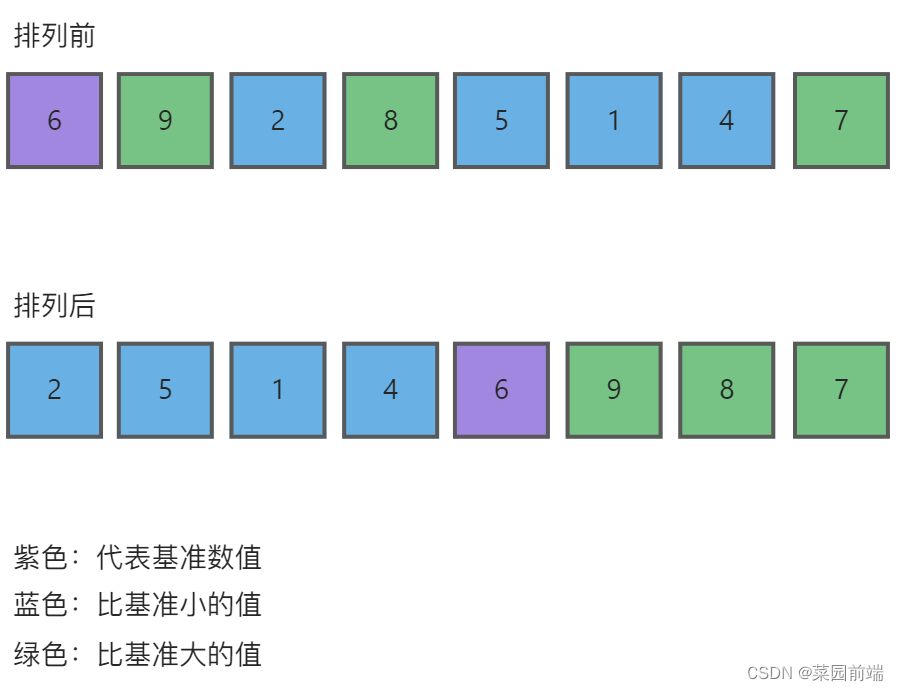
① 从数列中挑出一个元素,称为 “基准”(pivot),
② 重新排序数列,所有元素比基准值小的摆放在基准前面,所有元素比基准值大的摆在基准的后面(相同的数可以到任一边)。在这个分区退出之后,该基准就处于数列的中间位置。这个称为分区(partition)操作。
③ 递归地(recursive)把小于基准值元素的子数列和大于基准值元素的子数列排序。
递归到最底部时,数列的大小是零或一,也就是已经排序好了。这个算法一定会结束,因为在每次的迭代(iteration)中,它至少会把一个元素摆到它最后的位置去。
// 假设按照升序对array数组中[left, right)区间中的元素进行排序
void QuickSort(int array[], int left, int right)
{
if(right - left <= 1)
return;
// 按照基准值对array数组的 [left, right)区间中的元素进行划分
int div = partion(array, left, right);
// 划分成功后以div为边界形成了左右两部分 [left, div) 和 [div+1, right)
// 递归排[left, div)
QuickSort(array, left, div);
// 递归排[div+1, right)
QuickSort(array, div+1, right);
}上述为快速排序递归实现的主框架,发现与二叉树前序遍历规则非常像,同学们在写递归框架时可想想二叉树前序遍历规则即可快速写出来,后序只需分析如何按照基准值来对区间中数据进行划分的方式即可。将区间按照基准值划分为左右两半部分的常见方式有:
1. hoare版本

代码
int PartSort1(int* a, int begin, int end)
{
int left = begin, right = end;
int keyi = left;
while (left < right)
{
//右边先走,找比a[keyi]小的
while (left < right && a[right] >= a[keyi])
{
right--;
}
//左边先走,找比a[keyi]大的
while (left < right && a[left] <= a[keyi])
{
left++;
}
//交换左右边
Swap(&a[left], &a[right]);
}
//交换keyi与交点的值
Swap(&a[left], &a[keyi]);
keyi = left;
}
2. 挖坑法

代码
// 挖坑法
int PartSort2(int* a, int begin, int end)
{
int key = a[begin];
int piti = begin;
while (begin < end)
{
// 右边找小,填到左边的坑里面去。这个位置形成新的坑
while (begin < end && a[end] >= key)
{
--end;
}
a[piti] = a[end];
piti = end;
// 左边找大,填到右边的坑里面去。这个位置形成新的坑
while (begin < end && a[begin] <= key)
{
++begin;
}
a[piti] = a[begin];
piti = begin;
}
a[piti] = key;
return piti;
}3. 前后指针版本

代码
int PartSort3(int* a, int begin, int end)
{
int keyi = begin;
int cur = begin + 1;
int prev = begin;
// 加入三数取中的优化
int midi = GetMidIndex(a, begin, end);
Swap(&a[keyi], &a[midi]);
while (cur <= end)
{
if (a[cur] < a[keyi])
{
prev++;
Swap(&a[cur], &a[prev]);
}
cur++;
}
Swap(&a[begin], &a[prev]);
keyi = prev;
return keyi;
}
快速排序优化
1. 三数取中法选key
当我们知道这组无序数列的首和尾后,我们便可以求出这个无需数列的中间位置的数,我们只需要在首,中,尾这三个数据中,选择一个排在中间的数据作为基准值,进行快速排序,即可进一步提高快速排序的效率。那么为什么要取中间呢?我们可以假设待排序的数列是一组高度有序的数列,显然首极大可能是最小值,尾极大可能是最大值,此时如果我们选取一个排在中间的值,哪怕是在最坏的情况下,begin和end只需要走到中间位置,那么这个中间值的位置也就确定下来,而不需要begin或end指针要把整个数列遍历一边,从而大大提高快速排序的效率。即取数组最左端最右端以及数组中间三个数的中间数为分区点,减少采用左右端点碰到极端顺序的出现的最坏情况( 当选取左右端点,碰到数据有序,从大到小或是从小到大的情况 ,算法时间复杂度就会变成最坏时间复杂度)。
int GetMidIndex(int* a, int begin, int end) // 三数取中,优化算法,避免发生最坏的情况
{
int mid = (begin + end) / 2;
if (a[begin] < a[mid])
{
if (a[mid] < a[end])
{
return mid;
}
else if (a[begin] < a[end])
{
return end;
}
else
{
return begin;
}
}
else // (a[begin] >= a[mid])
{
if (a[mid] > a[end])
{
return mid;
}
else if (a[begin] < a[end])
{
return begin;
}
else
{
return end;
}
}
}2. 递归到小的子区间时,可以考虑使用插入排序
序列长度达到一定大小时,使用插入排序当快排达到一定深度后,划分的区间很小时,再使用快排的效率不高。当待排序列的长度达到一定数值后,可以使用插入排序。由《数据结构与算法分析》(Mark Allen Weiness所著)可知,当待排序列长度为5~20之间,此时使用插入排序能避免一些有害的退化情形。
void Qsort(int* a, int begin, int end)
{
if (begin >= end) return;
if (end - begin > 10)// 优化二:在递归到剩余数据量小于一定值的时候跳出递归,进行小数据量的插入排序
{
int keyi = PartSort3(a, begin, end);
// [begin, keyi-1] keyi [keyi+1, end]
Qsort(a, begin, keyi - 1);
Qsort(a, keyi + 1, end);
}
else
{
InsertSort(a + begin, end - begin + 1);
}
}快速排序非递归(用栈实现)
void QsortStack(int* a, int begin, int end)
{
ST st;
STInit(&st);
STPush(&st, end);
STPush(&st, begin);
while (!STEmpty(&st))
{
int left = STTop(&st);
STPop(&st);
int right = STTop(&st);
STPop(&st);
int keyi = PartSort3(a, left, right);
// [left, keyi-1] keyi[keyi+1, right]
if (keyi + 1 < right)
{
STPush(&st, right);
STPush(&st, keyi + 1);
}
if (left < keyi - 1)
{
STPush(&st, keyi - 1);
STPush(&st, left);
}
}
STDestroy(&st);
}快速排序的特性总结
1. 快速排序整体的综合性能和使用场景都是比较好的,所以才敢叫快速排序
2. 时间复杂度:O(N*logN)
3. 空间复杂度:O(logN)
4. 稳定性:不稳定
全部代码
//快速排序
int PartSort1(int* a, int begin, int end)
{
int left = begin, right = end;
int keyi = left;
while (left < right)
{
//右边先走,找比a[keyi]小的
while (left < right && a[right] >= a[keyi])
{
right--;
}
//左边先走,找比a[keyi]大的
while (left < right && a[left] <= a[keyi])
{
left++;
}
//交换左右边
Swap(&a[left], &a[right]);
}
//交换keyi与交点的值
Swap(&a[left], &a[keyi]);
keyi = left;
}
// 挖坑法
int PartSort2(int* a, int begin, int end)
{
int key = a[begin];
int piti = begin;
while (begin < end)
{
// 右边找小,填到左边的坑里面去。这个位置形成新的坑
while (begin < end && a[end] >= key)
{
--end;
}
a[piti] = a[end];
piti = end;
// 左边找大,填到右边的坑里面去。这个位置形成新的坑
while (begin < end && a[begin] <= key)
{
++begin;
}
a[piti] = a[begin];
piti = begin;
}
a[piti] = key;
return piti;
}
int GetMidIndex(int* a, int begin, int end) // 三数取中,优化算法,避免发生最坏的情况
{
int mid = (begin + end) / 2;
if (a[begin] < a[mid])
{
if (a[mid] < a[end])
{
return mid;
}
else if (a[begin] < a[end])
{
return end;
}
else
{
return begin;
}
}
else // (a[begin] >= a[mid])
{
if (a[mid] > a[end])
{
return mid;
}
else if (a[begin] < a[end])
{
return begin;
}
else
{
return end;
}
}
}
int PartSort3(int* a, int begin, int end)
{
int keyi = begin;
int cur = begin + 1;
int prev = begin;
// 加入三数取中的优化
int midi = GetMidIndex(a, begin, end);
Swap(&a[keyi], &a[midi]);
while (cur <= end)
{
if (a[cur] < a[keyi])
{
prev++;
Swap(&a[cur], &a[prev]);
}
cur++;
}
Swap(&a[begin], &a[prev]);
keyi = prev;
return keyi;
}
void Qsort(int* a, int begin, int end)
{
if (begin >= end) return;
if (end - begin > 10)// 优化二:在递归到剩余数据量小于一定值的时候跳出递归,进行小数据量的插入排序
{
int keyi = PartSort3(a, begin, end);
// [begin, keyi-1] keyi [keyi+1, end]
Qsort(a, begin, keyi - 1);
Qsort(a, keyi + 1, end);
}
else
{
InsertSort(a + begin, end - begin + 1);
}
}
void QsortStack(int* a, int begin, int end)
{
ST st;
STInit(&st);
STPush(&st, end);
STPush(&st, begin);
while (!STEmpty(&st))
{
int left = STTop(&st);
STPop(&st);
int right = STTop(&st);
STPop(&st);
int keyi = PartSort3(a, left, right);
// [left, keyi-1] keyi[keyi+1, right]
if (keyi + 1 < right)
{
STPush(&st, right);
STPush(&st, keyi + 1);
}
if (left < keyi - 1)
{
STPush(&st, keyi - 1);
STPush(&st, left);
}
}
STDestroy(&st);
}