😾 博客主页: 爱吃bug的猿
🚀博客专栏: 数据结构,C语言初阶进阶全流程讲解
😽😽😽如果喜欢博主的文章，可以给博主点波赞和关注加速博主更新

前言

• 希尔排序里的一部分和插入排序极其相似，了解插入排序及其复杂度（动图讲解）可点击此处
• 希尔排序分为两部分：预排序+插入排序

1. 代码思路

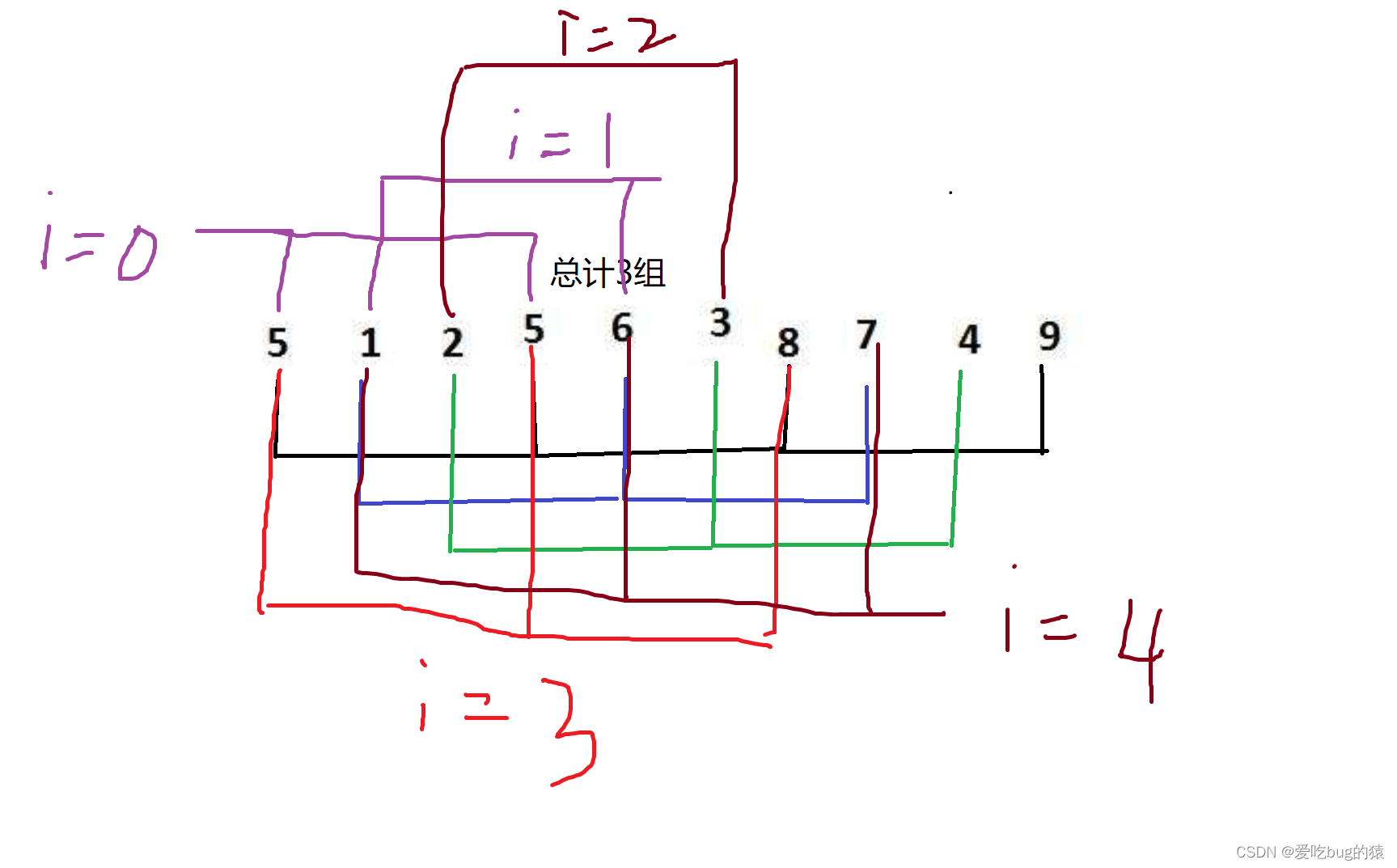
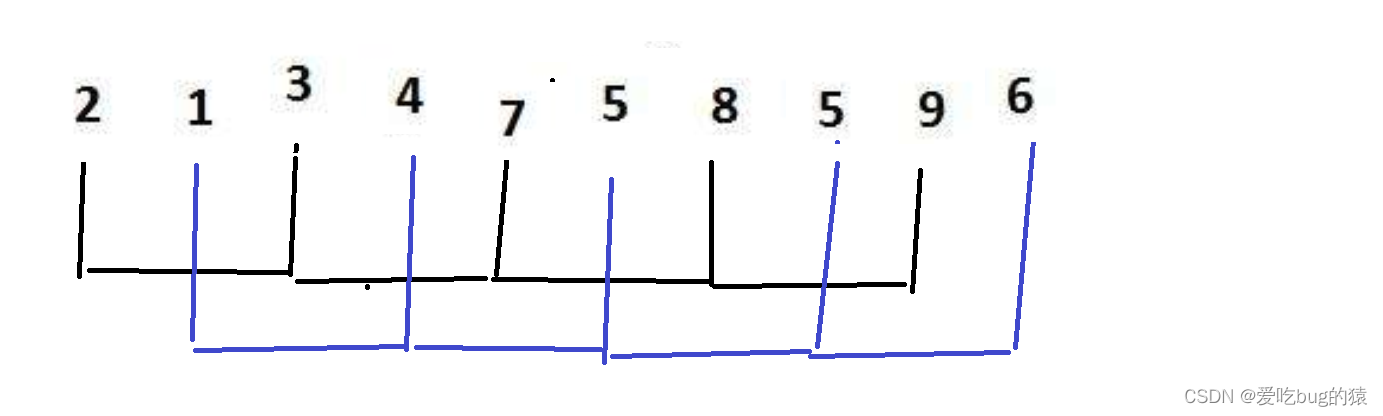
1. 选定一个整数作为增量gap，假设gap为3，则间隔为3的元素为一组，总计gap组
   
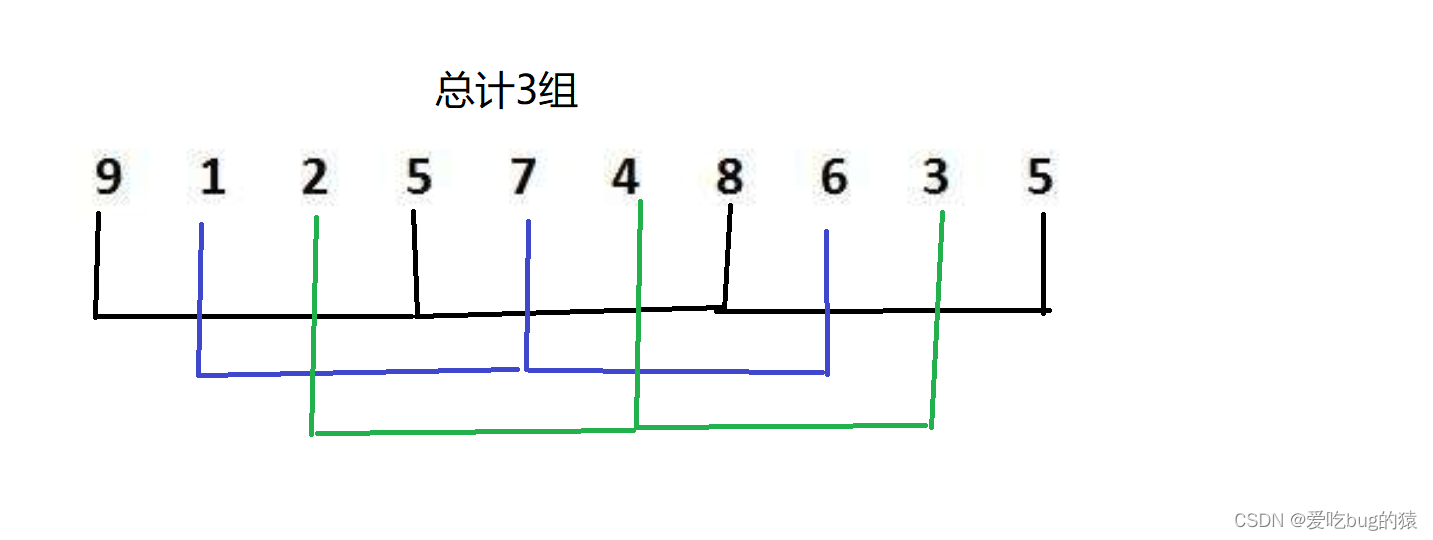
2. 接着对第一组（黑色）进行插入排序，第一组排完排第二组（蓝色），最后排第三组（黑色）
3. gap == 3 排序结果如下
   
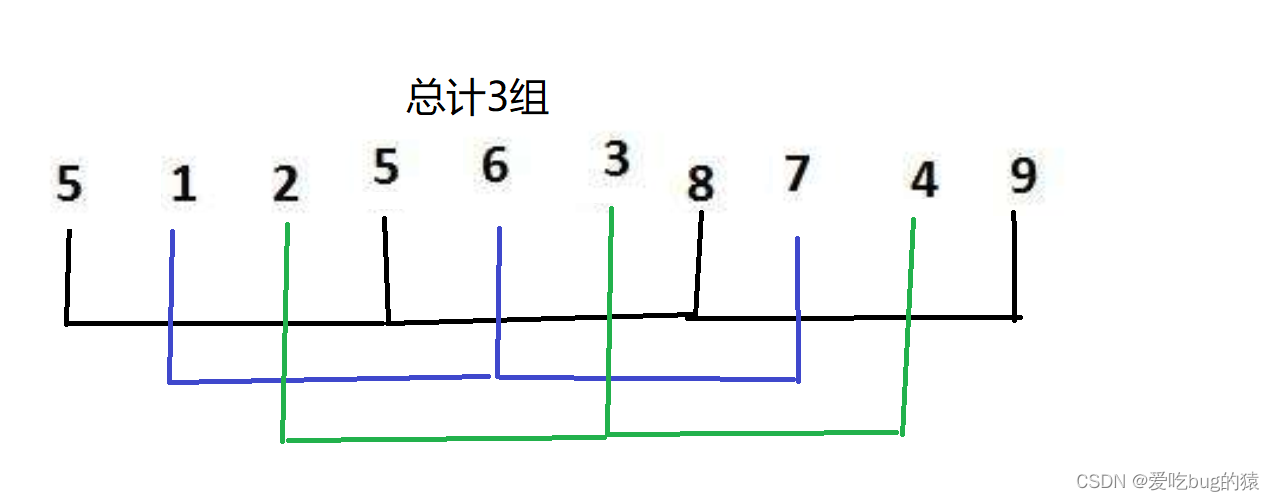
4. gap要减小（因为gap最终要减小为1，即增量为1的插入排序，经过这次排序后，才能保证数组真正有序），重复1,2步骤（gap > 1 是预排序，目的是让数组接近有序，gap == 1 排序后即有序），假设gap减小为2

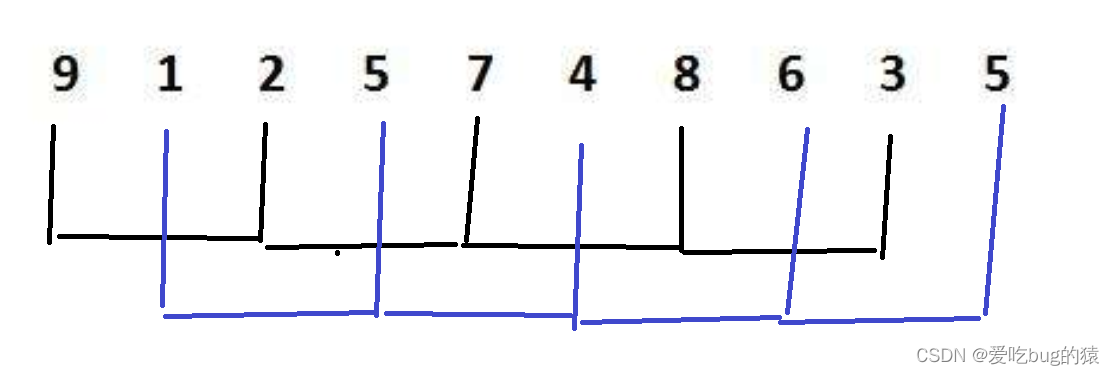
4. gap==2排序结果为

5. 最后gap == 1，插入排序即可
6. 目前gap的取法很多gap = gap/3 + 1（这里+1,是为了保证gap的最后的结果可以是1）,gap = gap/2

代码实现法1

void ShellSort(int*a,int n)
{
	int gap = n;
	while (gap > 1)
	{
		gap = gap / 3 + 1;
		//间隔为gap的元素分为一组，总计gap组，gap每次减小，直至gap == 1
		for (int j = 0; j < gap; j++)
		{//选出gap组的其中一组
		for (int i = j; i < n - gap; i += gap)
		{//对gap组的其中一组进行排序
		int end = i;
			int tmp = a[end + gap];
			while (end >= 0)
			{
				if (a[end] > tmp)
				{
					a[end + gap] = a[end];
					end -= gap;
				}
				else
				{
					break;
				}
			}
			a[end + gap] = tmp;
		}

		}
		}
	}

代码实现法2（不想用tmp变量可以不用）

void ShellSort(int* a, int n)
{
	int gap = n;
	while (gap > 1)
	{
		gap = gap / 3 + 1;
		//间隔为gap的元素分为一组，总计gap组，gap每次减小，直至gap == 1
		for (int j = 0; j < gap; j++)
		{//选出gap组的其中一组
			int tmp = 0;
			for (int i = j; i < n - gap; i += gap)
			{//对gap组的其中一组进行排序
				int end = i;
				while (end >= 0)
				{
					if (a[end] > a[end + gap])
					{
						int tmp = a[end + gap];
						a[end + gap] = a[end];
						a[end] = tmp;
						end -= gap;
					}
					else
					{
						break;
					}
				}
			}

		}
	}
}

代码实现法3（从三层循环变为两层循环）

void ShellSort(int*a,int n)
{
	int gap = n;
	while (gap > 1)
	{
		gap = gap / 3 + 1;
		for (int i = 0; i < n - gap; i++)
		{
			int end = i;
			int tmp = a[end + gap];

			while (end >= 0)
			{
				if (a[end] > a[end + gap])
				{
					a[end + gap] = a[end];
					end -= gap;
				}
				else
				{
					break;
				}
				a[end + gap] = tmp;

			}


		}
	}
	}

• 这样改的画其实是多组并排即多组一块排序
  

希尔排序的时间复杂度(O(n^1.3))

• 希尔排序的时间复杂度其实是算不出准确数值的，但我们能探讨一下到底是因为什么才算不出来

• 当gap很大时，假设gap = n / 3，每组插入次数为 1+2,总计gap组，则为n，所以时间复杂度为O(n)
• 当gap很小时，因为gap = gap /3，每次循环gap越来越小，最后gap很小时，数组已经接近有序，时间复杂度也为O(n)
• 假设gap为n/3，总计n/gap组,那么每组3个数组
• 

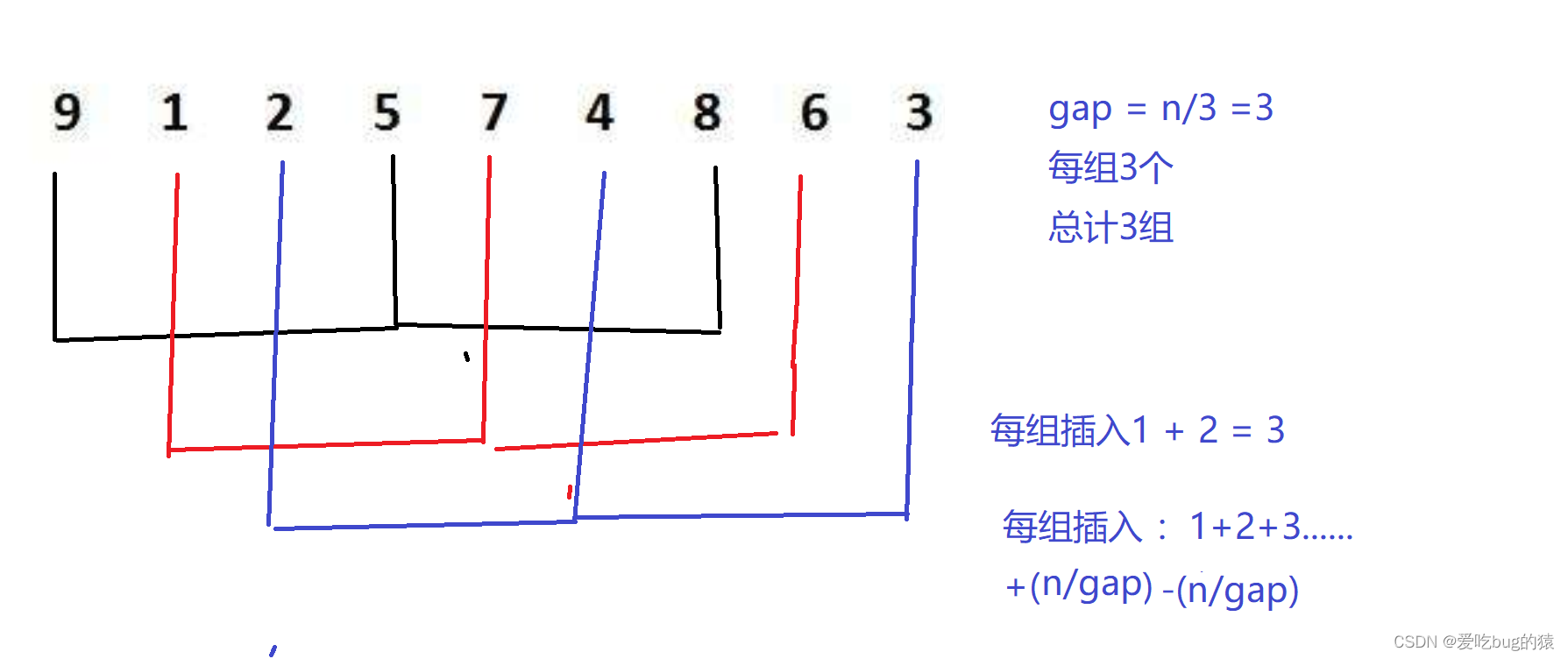
每组插入（次数）：1+2+3+…+( n / gap) - ( n / gap)
总的插入次数：gap（1+2+3+…+(n / gap) - ( n / gap))
假设gap = gap / 3(gap = gap /3 + 1,1忽略点)
则gap = n/3
gap = n /9
gap = n / 27
将gap带入也是可以算的，但是随着gap的减小，数组前面的数组逐渐有序，它不是总是最坏情况下的（上面算的最坏情况下的），当gap为1时，如果还是最坏情况下计算的话，那么总插入次数为1+2+3+…+n - n 约等于N^2 - N即 N方，结果显然不是这样的
所以最后估计结果O(n^1.3)