1.Matlab函数linprog()的使用
1.1 Matlab基本描述

1.2 函数linprog()
三种表达形式
- [x,fval] = linprog(c,A,b)
- [x,fval] = linprog(c,A,b,Acq,bcq)
- [x,fval]=linprog(c,A,b,Aeq,beq,lb,ub)
其中
- x返回的是决策向量的取值,
- fval返回的是目标函数的最优值,
- c为价值向量,
- A,b对应的是线性不等式约束,
- Aeq,beq对应的是线性等式约束,
- lb和b分别对应的是决策向量的下界向量和上界向量
1.3 求解例子1
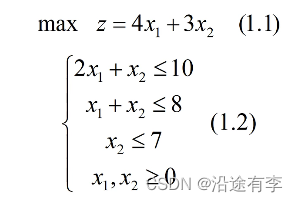
step1改写目标函数
- 目标函数改写为(-4 x 1 x_1 x1 -3 x 2 x_2 x2)
step2约束条件
- 不等式
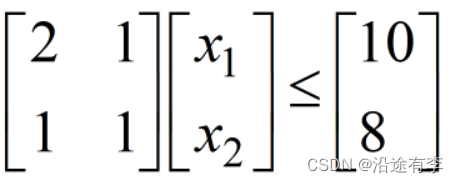
- 上下界约束可直接写。
step3编程
c=[-4;-3];
a=[2 1;
1 1];
b=[10;8];
lb=[0 0];
ub=[inf 7];
[x,y]=linprog(c,a,b,[],[],lb,ub);%无等式约束,但是也得写[],否则报错
x;
y=-y;
结果

1.3 求解例子2
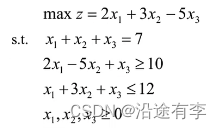
step1改写目标函数
- matlab优化函数只认识min,所以把目标函数改写为(-2
x
1
x_1
x1 -3
x
2
x_2
x2+5
x
3
x_3
x3)
从而可知列向量c=[-2;-3;5]
step2改写约束条件
- 等式:
aeq=[1;1;1] - 不等式:
把≥改为≤,把两个不等式约束一起写为矩阵形式。

step3编程
c=[-2;-3;5];
a=[-2 5 -1;
1 3 1];
b=[-10;12];
aeq=[1 1 1];
beq=7;
lb=[0 0 0];
[x,y]=linprog(c,a,b,aeq,beq,lb);
x;
y=-y;
结果

2 数模规划问题1——投资收益与风险
2.1 题目

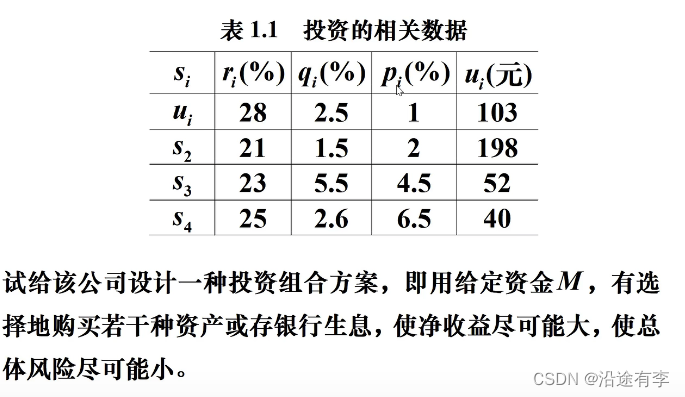
2.2 符号规定

3 模型一
3.1 分析

3.2 建模
本来是一个多目标规划问题,然后他把风险转为了约束条件,变为了单目标优化。
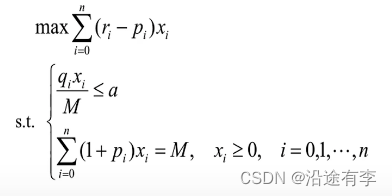
代入数据

就是相当于每间隔0.001做一次规划
3.3 求解
主要看一下不等式约束的矩阵形式

编程
a=0;
i=1;
hold on%一定要写
while a<0.05
c=[-0.05;-0.27;-0.19;-0.185;-0.185];
A=[zeros(4,1),diag([0.025,0.015,0.055,0.026])];%不等式
b=a*ones(4,1);%不等式
Aeq=[1,1.01,1.02,1.045,1.065];%等式
beq=1;%等式
LB=zeros(5,1);
[x,Q]=linprog(c,A,b,Aeq,beq,LB);
Q=-Q;
m(i)=Q;%每次计算的值
for j=1:5
mm(i,j)=x(j);%每次的投资方案
end
plot(a,Q,'*k');
a=a+0.001;
i=i+1;
end
xlabel('a');
ylabel('Q');
结果
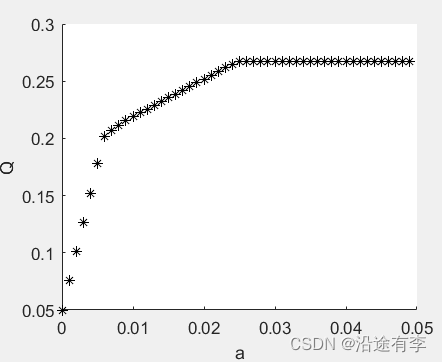
然后再去对结果做一个分析。
主要来自:B站【零基础教程】老哥:数学建模算法、编程、写作和获奖指南全流程培训!