衡量两个变量线性相关程度。先画散点图看是否为线性相关，相关系数才有用。

总体：要考察对象的全部个体

样本：从总体中所抽取的一部分个体

用样本的统计量估计总体的统计量

总体Person相关系数

协方差Cov(X,Y)反映X、Y的相关性

Person相关系数剔除了两个变量量纲的影响 

ρ_xy=Cov（X，Y）/ σ_x * σ_y 

 样本Person相关系数

ρ绝对值越接近于1，散列图越接近一条直线，相关性越大。

若XY无关，则ρ为0，反之不能推。

相关系数大小可以按照背景自定义。

验证变量的线性相关性：

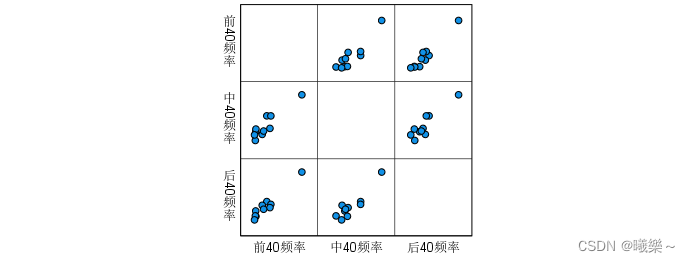
        导入数据至SPSS中，图形-旧对话框-散点图/点图，做出数据之间的图，若图是以下这种斜着的一条就是线性的：

 在MATLAB中计算：最小值，最大值，平均数等。得到描述性统计RESULT

MIN=min(A);
MAX=max(A);
MEAN=mean(A);
MEDIAN=median(A);
SKEWNESS=skewness(A);
KURTOSIS=kurtosis(A);
STD=std(A);
RESULT=[MIN;MAX;MEAN;MEDIAN;SKEWNESS;KURTOSIS;STD]
%RESULT存放描述性统计

[R,p]=corrcoef(A)

R存放相关系数

---

假设检验

        自己提出假设，验证自己的假设是否正确。

置信水平β=1-α：假设成立的概率（一般用90%，95%，99%）

α显著性水平：发生小概率事件（拒绝原假设的概率）

概率密度函数f(x):x发生在此的概率强度   1.f(x)>=0   2.在负无穷到无穷的积分为1。

累计密度函数F(x):F(x)<=P(X<x)

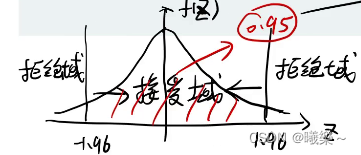
接受域：置信水平内

拒绝域：其他地方。

概率P 

 

第一步：确定原假设H0和备择假设H1（完全相反的两个假设）

        双侧检验：~=

        单侧检验：>或<

第二步：在原假设成立的条件下，自己构造分布（N、t、F、卡方分布）

        统计量只能包含假设的一个未知量Z
第三步：画概率密度函数f(x)

第四步：给一个置信水平β ，求出接受域（查表或用matlab算）

 第五步：用已知样本数据带入计算统计量，得到检验值，若检验值在接受域内则接受原假设，反之拒绝。

双侧检验求出的P值要×2再与显著性水平α比较。

---

显著性检验

相关系数=0则不相关。

显著性检验：检验0和相关系数的差异 

        相关性显著--相关

        相关性不显著--不相关。

 计算出Person相关系数r，检验它是否显著的异于0：

第一步：原定假设H0：r=0，备择假设：H1：r~=0

第二步：在一定的条件下可以构造统计量

 （t分布是标准正态分布的特例，n趋于无穷时即为标准正态分布）

第三步：将r代入公式得到检验值。

第四步：画出分布的概率密度函数pdf，给定一个置信水平β，找到临界值，画出统计量的接受域和拒绝域

%x=起始值：步长：终值;
%y=tpdf(x,自由度);
plot(x,y,'-')
grid on%画网格

第五步： 检验值在拒绝域内，H1成立；在接受域内，H0成立。

p值判断法

        得到检验值t*，计算对应概率。

tcdf计算累计概率密度函数。

%检验值对应的p值=（1-tcdf(检验值,自由度)*2）
%双侧检验的p值要乘以2

p<0.01，在99%的置信水平上拒绝原假设；p>0.01，在99%的置信水平无法拒绝原假设

p<0.05，在95%的置信水平上拒绝原假设；p>0.05，在95%的置信水平无法拒绝原假设；

p<0.10，在90%的置信水平上拒绝原假设。p>0.10，在90%的置信水平无法拒绝原假设。

本例拒绝原假设意味着皮尔逊相关系数显著的异于0

显著性标记，空不显著 *在90%上越显著异于0 **95% ***99%

SPSS做相关性分析很方便。