目录

求极限的方式：

利用洛必达法则求极限

n阶可导的理解

 几个常用的泰勒公式

---

求极限的方式：

利用洛必达法则求极限

 

 洛必达法则适用于分子分母的极限同为0或者同为无穷的形式。

我们洛必达法则相当于对分子分母同时求导，所以要要求再x0的去心邻域内可导，使用过洛必达之后，g(x)的一阶导数就是分母，所以分母不能等于0.

使用过洛必达之后的极限应该存在或者为无穷。

洛必达法则虽然理论上只适用于0比0或者无穷比无穷，但以下的这些形式都可以考虑用洛必达法则：

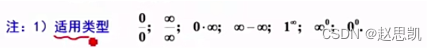
 我们的思路是这样的：

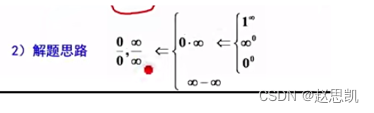
 当然对于1的无穷次方，我们可以用我们之前总结的方法：更加简便

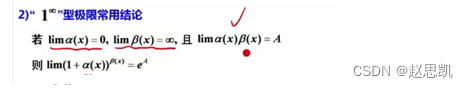
 我们举一个例子：

 我们举一个例子：

 

 

 

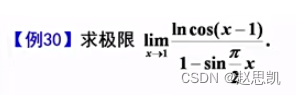
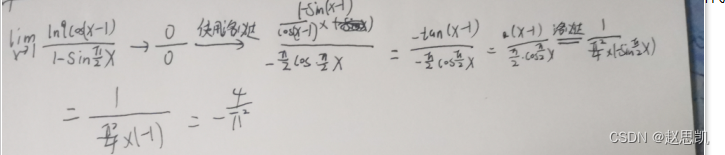
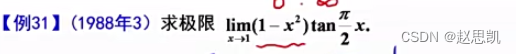
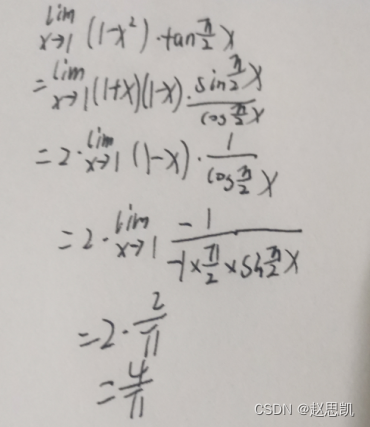
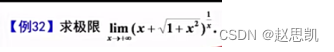
 我们先看函数的形式，函数是无穷的0次方的形式，并且函数的类型是幂函数与指数函数的结合体，对于幂指函数，常用的方法就是取对数：

 

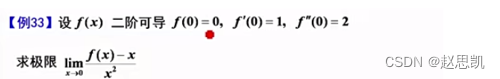
我们常说的函数可导是函数一阶可导，函数一阶可导可以推出原函数连续，则函数二阶可导可以推出一阶导函数连续。

 

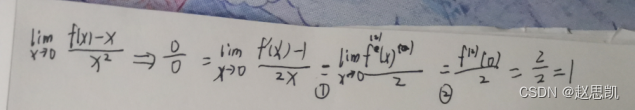
 这种写法其实是错误的，错误点2：

只有一阶导函数和原函数是连续的，二阶导函数并不是连续的，所以不能用二阶导数这一点的函数来代替具体值。

错误点1：对于洛必达法则，我们要保证使用洛必达之后的式子是有明显极限的，所以在这个题目中，我们只能使用一次洛必达法则。

正确的写法：

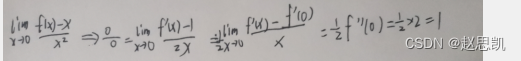
 我们这里使用的是导数的定义的方法。

n阶可导的理解

函数在某一区间n阶可导的含义就是n-1阶导函数包括之前的函数都是连续的，函数是n阶可导的话，我们最多只能使用n-1次洛必达法则。

当题设中写出函数在区间内n阶连续可导，就表明n阶函数及之前的函数都是连续的，并且我们最多可以使用n次洛必达法则。

方法2：

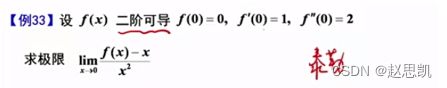
我们可以使用泰勒公式，对于求极限的题目，我们可以使用第一种泰勒公式：

 

对于这类题目，我们进行总结：

1：我们看分母的最高次项是二次，我们只需使用泰勒公式到出现二次项即可。

2：题设中，关于哪一点出现的条件最多，我们就使用哪一点的泰勒公式，一般都是给的0点。 

 几个常用的泰勒公式

 对于tanx和arcsinx的泰勒公式，我们可以这样写：

 

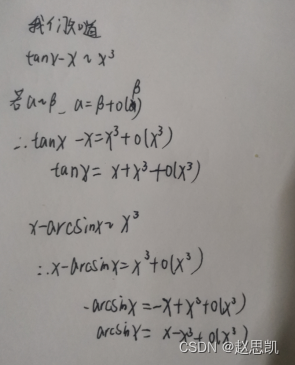
我们可以使用泰勒公式：

分母的最高此项是4次项。

 

 方法2：

 

 

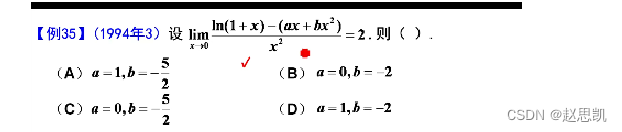
 方法1：使用泰勒公式：

 方法2：

 解法3：