算法竞赛备赛之经典基础算法训练提升，暑期集训营培训

news2024/11/17 21:34:42

 

目录

1.排序

1.1.快速排序

1.2.归并排序

2.二分

2.1.整数

2.2.浮点数

3.高精度

3.1.高精度加法

3.2.高精度减法

3.3.高精度乘法

3.4.高精度除法

4.前缀和

5.差分

6.双指针算法

7.位运算

8.离散化

8.1.unique函数实现

9.区间合并

1.排序

1.1.快速排序

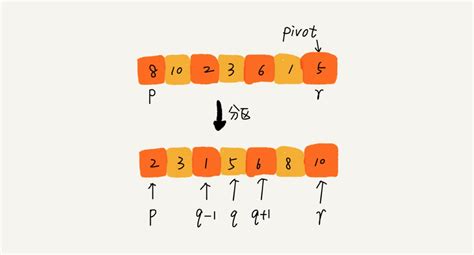
快速排序的基本思想来自于分治。

首先，确定分界点的方法：

  1. q[left];

  2. q[(left + right) / 2];

  3. q[right];

  4. 随机

第二步，则是调整区间，按照相应的要求，将数值划分为两部分。

第三步，递归处理左右两段数值。

使用两个指针分别指向左右两端，判断左右两端与指定的分界值x之间的关系，做出相应的调整。

快速排序模板：

#include<iostream>
using namespace std;
​
const int N = 1e6 + 10;
​
int n;
int q[N];
​
void quick_sort(int q[], int l, int r)
{
    if(l >= r) return;
    
    int x = q[l], i = l-1, j = r+1;
    while(i < j)
    {
        do i++;while(q[i] < x);
        do j--;while(q[j] > x);
        if(i < j) swap(q[i], q[j]);
    }
    quick_sort(q, l, j);
    quick_sort(q, j+1, r);
}
​
int main()
{
    scanf("%d", &n);
    for(int i = 0;i < n; i++)
    {
        scanf("%d", &q[i]);
    }
    
    quick_sort(q, 0, n-1);
    
    for(int i = 0;i < n; i++)
    {
        printf("%d ", q[i]);
    }
    return 0;
}

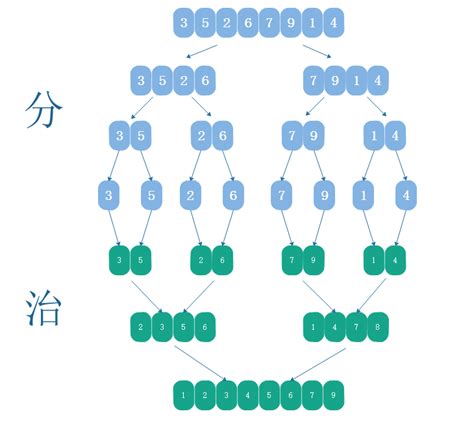
1.2.归并排序

也是通过分治的思想，将数组分成left和right

  1. 确定

  2. 递归排序left、right

  3. 归并——合二为一

​

wAAACH5BAEKAAAALAAAAAABAAEAAAICRAEAOw== 编辑 
#include<iostream>
​
using namespace std;
​
#define N 10000
int n;
int q[N], tmp[N];
​
void merge_sort(int q[], int l, int r)
{
    if(l >= r) return;
    int mid = l + r >> 1;
    merge_sort(q, l, mid), merge_sort(q, mid + 1, r);
    
    int k = 0, i = l, j = mid + 1;
    while(i <= mid && j <= r)
    {
        if(q[i] <= q[j]) tmp[k++] = q[i++];
        else tmp[k++] = q[j++];
    }
    
    while(i <= mid) tmp[k++] = q[i++];
    while(j <= r) tmp[k++] = q[j++];
    
    for(i = l, j = 0;i <= r; i++, j++)
    {
        q[i] = tmp[j];
    }
}
​
int main()
{
    scanf("%d", &n);
    for(int i = 0;i < n; i++)
    {
        scanf("%d", &q[i]);
    }
    
    merge_sort(q, 0, n - 1);
    
    for(int i = 0;i < n; i++)
    {
        printf("%d ", q[i]);
    }
    
    return 0;
}

vector容器的模板

void merge_sort(vector<int>& arr, int left, int right) {
    if (left < right) {
        int mid = (left + right) / 2;
        merge_sort(arr, left, mid);
        merge_sort(arr, mid + 1, right);
        merge(arr, left, mid, right);
    }
}
​
void merge(vector<int>& arr, int left, int mid, int right) {
    vector<int> left_arr(arr.begin() + left, arr.begin() + mid + 1);
    vector<int> right_arr(arr.begin() + mid + 1, arr.begin() + right + 1);
    int i = left - 1;
    int j = mid;
    int k = 0;
    while (k < right - left + 1) {
        if (j == right) {
            arr[++i] = left_arr[++k];
        } else if (left_arr[++k] <= right_arr[j]) {
            arr[++i] = left_arr[k];
        } else {
            arr[++i] = right_arr[j];
        }
    }
}

其中，merge_sort函数是递归函数，将待排序的数组分为左右两部分，再分别调用merge_sort函数进行排序。merge函数则是将左右两个已排序的数组合并成一个有序数组。

2.二分

通过某一条性质，每一次从中间进行分割，一半满足条件，一般不满足。不满足的那一部分就直接毙掉，满足的那一部分在调用二分法进行框定界限，从而使确定值越来越接近。

2.1.整数

前提是要排好序的，且必须要有解。

整数二分法题目 - 数的范围：

#include<iostream>
using namespace std;
​
const int N = 1e5 + 10;
​
int n, m;
int q[N];
​
int main()
{
    scanf("%d%d", &n, &m);
    for(int i = 0;i < n; i++)
    {
        scanf("%d", &q[i]);
    }
    
    while(m--)
    {
        int x;
        scanf("%d", &x);
        
        int l = 0,r = n - 1;
        while(l < r)
        {
            int mid = l + r >> 2;
            if(q[mid] >= x) r = mid;
            else l = mid + 1;
        }
        
        if(q[l] != x) cout << "-1 -1" << endl;
        else
        {
            cout << l << ' ';
            int l = 0, r = n - 1;
            while(l < r)
            {
                int mid = l + r >> 1;
                if(q[mid] <= x) l = mid;
                else r = mid - 1;
            }
            
            cout << l << endl;
        }
    }
    
    return 0;
}

2.2.浮点数

开平方：

#include<iostream>
using namespace std;
​
int main()
{
    double x;
    scanf("%lf", &x);
    
    double l = 0, r = x;
    while(r - l > 1e-8)//经验值，比要求小数多两位
    {
        double mid = (l + r) / 2;
        if(mid * mid >= x) r = mid;
        else l = mid;
    }
    printf("%lf", l);
    return 0;
}

3.高精度

3.1.高精度加法

两个正整数相加

#include<iostream>
#include<vector>
using namespace std;
​
const int N = 1e6 + 10;
​
vector<int> add(vector<int> &A, vector<int> &B)
{
    vector<int> C;
    
    int t = 0;
    for(int i = 0;i < A.size() || i < B.size(); i++)
    {
        if(i < A.size()) t += A[i];
        if(i < B.size()) t += B[i];
        C.push_back(t%10);
        t /= 10;
    }
    if(t) C.push_back(1);
    return C;
}
​
int main()
{
    string a, b;
    vector<int> A, B;
    
    cin >> a >> b;//a = '123456'
    for(int i = a.size() - 1;i >= 0; i--)
    {
        A.push_back(a[i] - '0');//A = [6,5,4,3,2,1]
    }
    for(int i = b.size() - 1;i >= 0; i--)
    {
        B.push_back(b[i] - '0');
    }
    
    auto c = add(A, B);
    
    for(int i = c.size() - 1;i >= 0; i--)
    {
        printf("%d",c[i]);
    }
    return 0;
}

3.2.高精度减法

两个正整数相减。

首先要考虑到正负号，当小数减大数的时候，一定是负的；

其次是一位不够，向上借位。

#include<iostream>
#include<vector>
​
using namespace std;
​
bool cmp(vector<int> &A, vector<int> &B)
{
    if(A.size() != B.size()) return A.size() > B.size();
    for(int i = A.size() - 1;i >= 0; i--)
    {
        if(A[i] != B[i]) return A[i] > B[i];
    }
    return true;
}
​
vector<int> sub(vector<int> &A, vector<int> &B)
{
    vector<int> C;
    int t = 0;
    for(int i = 0;i < A.size(); i++)
    {
        t = A[i] - t;
        if(i < B.size()) t -= B[i];
        C.push_back((t + 10) % 10);
        if(t < 0) t = 1;
        else t = 0;
    }
    while(C.size() > 1 && C.back() == 0)
        C.back();//去掉前导0
    return C;
}
​
int main()
{
    string a, b;
    vector<int> A, B;
    
    cin >> a >> b;
    for(int i = a.size() - 1;i >= 0; i--)
    {
        A.push_back(a[i] - '0');
    }
    for(int i = b.size() - 1;i >= 0; i--)
    {
        B.push_back(b[i] - '0');
    }
    
    if(cmp(A, B))
    {
        auto c = sub(A, B);
        for(int i = c.size() - 1;i >= 0; i--)
        {
            printf("%d",c[i]);
        }
    }
    else
    {
        auto c = sub(B, A);
        printf("-");
        for(int i = c.size() - 1;i >= 0; i--)
        {
            printf("%d",c[i]);
        }
    }
    return 0;
}

3.3.高精度乘法

两个正整数相乘，长整数乘上短整数的代码。

#include<iostream>
#include<vector>
​
using namespace std;
​
vector<int> mul(vector<int>&A, int b)
{
    vector<int> C;
    
    int t = 0;//进位
    for(int i = 0;i < A.size() || t; i++)
    {
        if(i < A.size()) t += A[i] * b;
        C.push_back(t % 10);
        t /= 10;
    }
    return C;
}
​
int main()
{
    string a;
    int b;
    cin >> a >> b;
    vector<int>A;
    
    for(int i = a.size() - 1;i >= 0; i--)
    {
        A.push_back(a[i] - '0');
    }
    
    auto C = mul(A, b);
    
    for(int i = C.size() - 1;i >= 0; i--)
    {
        printf("%d",C[i]);
    }
    
    return 0;
}

3.4.高精度除法

高精度的整数除以低精度的整数。

#include<iostream>
#include<vector>
#include<algorithm>
using namespace std;
​
// A/b，商是C，余数是r
vector<int> div(vector<int> &A, int b, int &r)
{
    vector<int> C;//商
    r = 0;
    for(int i = A.size() - 1;i >= 0; i--)
    {
        r = r * 10 + A[i];
        C.push_back(r / b);
        r %= b;
    }
    
    reverse(C.begin(), C.end());
    while(C.size() >= 1 && C.back() == 0) C.pop_back();
    
    return C;
}
​
int main()
{
    string a;
    int b;
    cin >> a >> b;
    
    vector<int> A;
    for(int i = a.size() - 1;i >= 0; i--)
    {
        A.push_back(a[i] - '0');
    }
    
    int r;
    auto C = div(A, b, r);
    
    for(int i = C.size() - 1;i >= 0; i--)
    {
        printf("%d",C[i]);
    }
    cout << endl << r << endl;
    
    return 0;
}

4.前缀和

Si = a1 + a2 + a3 + ..... + an (注意：S0 = 0)

如何求Si：

for(int i = 1;i <= n; i++)
{
    S[i] = S[i-1] + a[i];
}

作用：[l, r] 时间复杂度O(n)

用一次运算来计算任意段内的值：Sr - Sl-1

#include<iostream>
using namespace std;
​
const int N = 100010;
​
int n, m;
int a[N], s[N];
​
int main()
{
    ios::sync_with_stdio(false);//对cin的判断
    
    scanf("%d%d",&n, &m);
    for(int i = 1;i <= n; i++)
    {
        scanf("%d", &a[i]);
    }
    
    for(int i = 1;i <= n; i++)
    {
        s[i] = s[i-1] + a[i];
    }
    
    while(m--)
    {
        int l, r;
        scanf("%d%d", &l, &r);
        printf("%d\n", s[r] - s[l-1]);
    }
    return 0;
}

图的面积裁剪问题

求和S[i] [j]，这时候能用我们熟知的割补法来进行计算

S[x2][y2] - S[x2][y1-1] - S[x1-1][y2] + S[x1- 1][y1 -1];

这一块还是简单的，代码也是好写的

#include<iostream>
using namespace std;
​
const int N = 1010;
​
int n, m, q;
int a[N][N], s[N][N];
​
int main()
{
    scanf("%d%d%d", &n, &m, &q);
    for(int i = 1;i <= n; i++)
    {
        for(int j = 1;j <= m; j++)
        {
            scanf("%d", &a[i][j]);
        }
    }
    
    for(int i = 1;i <= n; i++)
    {
        for(int j = 1;j <= m; j++)
        {
            s[i][j] = s[i-1][j] + s[i][j-1] - s[i-1][j-1] + a[i][j];//求前缀和
        }
    }
    
    while(q--)
    {
        int x1, y1, x2, y2;
        scanf("%d%d%d%d", &x1, &y1, &x2, &y2);
        printf("%d", s[x2][y2] - s[x2][y1-1] - s[x1-1][y2] + s[x1-1][y1 -1]);//算部分矩阵和
    }
    return 0;
}

5.差分

是前缀和的逆运算

a1, a2, .... an 构造b1, b2, ... , bn

b1 =a1 b2 = a2 - a1 bn = an - an-1

a就是b的前缀和，b就是a的差分

差分题目：

输入一段长度为n的整数序列

接下来输入m个操作，每个操作包含三个整数l，r，c，表示将序列中[l,r]之间的每个数加上c，输出进行完所有操作后的序列。

#include<iostream>
using namespace std;
​
const int N = 100010;
​
int n, m;
int a[N], b[N];
​
void insert(int l, int r, int c)
{
    b[l] += c;
    b[r + 1] -= c;
}
​
int main()
{
    scanf("%d%d", &n, &m);
    for(int i = 1;i <= n; i++)
    {
        scanf("%d", &a[i]);
    }
    for(int i = 1;i <= n; i++)
    {
        insert(i, i, a[i]);
    }
    
    while(m--)
    {
        int l,r,c;
        scanf("%d%d%d", &l, &r, &c);
        insert(l, r, c);
    }
    
    for(int i = 1;i <= n; i++)
    {
        b[i] += b[i-1];
    }
    
    for(int i = 1;i <= n; i++)
    {
        printf("%d ", b[i]);
    }
    return 0;
}

我们上面的代码是一维的差分，接下来我们来构造一个差分矩阵。

b[x1][y1] += c;
b[x2+1][y1] -= c;
b[x1][y2+1] -= c;
b[x2+1][y2+1] += c;

实现代码：

#include<iostream>
using namespace std;
​
const int N = 1010;
​
int n, m, q;
int a[N][N], b[N][N];
​
void insert(int x1, int y1, int x2, int y2, int c)
{
    b[x1][y1] += c;
    b[x2+1][y1] -= c;
    b[x1][y2+1] -= c;
    b[x2+1][y2+1] += c;
}
​
int main()
{
    scanf("%d%d%d",&n, &m, &q);
    
    for(int i = 1;i <= n; i++)
    {
        for(int j = 1;j <= m; j++)
        {
            scanf("%d", &a[i][j]);
        }
    }
    
    for(int i = 1;i <= n; i++)
    {
        for(int j = 1;j <= m; j++)
        {
            insert(i, j, i, j, a[i][j]);
        }
    }
    
    while(q--)
    {
        int x1, x2, y1, y2, c;
        scanf("%d%d%d%d%d",&x1, &y1, & x2, &y2, &c);
        insert(x1, y1, x2, y2, c);
    }
    
    for(int i = 1;i <= n; i++)
    {
        for(int j = 1;j <= m; j++)
        {
            b[i][j] += b[i-1][j] + b[i][j-1] -b[i-1][j-1];
        }
    }
    
    for(int i = 1;i <= n; i++)
    {
        for(int j = 1;j <= m; j++)
        {
            printf("%d ",b[i][j]);
        }
    }
    
    return 0;
}

6.双指针算法

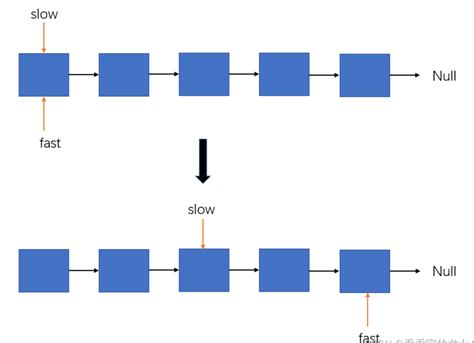
for(int i = 0, j = 0;i < n; i++)
{
    while(j < i && check(i, j)) j++;
    
    //每道题目的具体思路
}

核心思想：

for(int i = 0;i < n; i++)
{
    for(in j = 0;j < n; j++)
}
//算法复杂度O(n^2)

双指针算法能将上述的朴素算法优化到O(n)

输出字符串的每个单词：

前提每个单词间只有一个空格。

#include<iostream>
#include<string.h>
using namespace std;
​
int main()
{
    char str[1000];
    
    gets(str);
    
    int n = strlen(str);
    
    for(int i = 0;i < n; i++)
    {
        int j = i;
        while(j < n && str[j] != ' ')
        {
            j++;
        }
        
        //本题的具体逻辑
        for(int k = i;k < j; k++)
            cout << str[k];
        cout << endl;
        
        i = j;
    }
    return 0;
}

最长连续不重复子序列：

给定一个长度为n的整数序列，请找出最长的不包含重复数字的连续序列，输出它的长度。

//朴素算法

for(int i = 0;i < n; i++)
{
    for(int j = 0;j <= i; j++)
    {
        if(check(j, i))
        {
            res = max(res, i - j + 1);
        }
    }
}

//双指针算法

for(int i = 0, j = 0;i < n; i++)
{
    while(j <= i && check(j, i)) j++;
    res = max(res, i - j + 1);
}

j：j往左最远能到的位置

题目代码模板：

#include<iostream>
​
using namespace std;
​
const int N = 100010;
​
int n;
int a[N], s[N];
​
int main()
{
    scanf("%d", &n);
    for(int i = 0;i < n; i++)
    {
        scanf("%d", &a[i]);
    }
    
    int res = 0;
    for(int i = 0, j = 0;i < n; i++)
    {
        s[a[i]]++;
        while(s[a[i]] > 1)
        {
            s[a[j]]--;
            j++;
        }
        
        res = max(res, i - j + 1);
    }
    
    printf("%d\n", res);
    
    return 0;
}

7.位运算

n的二进制表示第k位

  1. 先把第k位数字移到最后一位 n >> k

  2. 再观察个位的数字 x & 1

  3. lowbit(x)：返回x的最后一位 x & -x = x & (~x + 1)

#include<iostream>
using namespace std;
​
int lowbit(int x)
{
    return x & -x;
}
​
int main()
{
    int n;
    cin >> n;
    while(n--)
    {
        int x;
        cin >> x;
        
        int res = 0;
        while(x) x -= lowbit(x), res++;//每次减去x的最后一位
        
        cout << res << ' ';
    }
    
    return 0;
}

数据在内存中以2进制的形式存储 对于整数来说： 整数二进制有3种表示形式：原码、反码、补码 正整数：原码、反码、补码相同 负整数：原码、反码、补码要进行计算的 按照数据的数值直接写出的二进制序列就是原码 原码的符号位不变，其他位按位取反，得到的就是反码 反码+1，得到的就是补码

存储举例1：

int a = -10;

1000 0000 0000 0000 0000 0000 0000 1010 - 原码

1111 1111 1111 1111 1111 1111 1111 0101 - 反码

1111 1111 1111 1111 1111 1111 1111 1110 - 补码

FFFFFFF6-内存存储

内存存补码。

#include<iostream>
using namespace std;
​
int lowbit(int x)
{
    return x & -x;
}
​
int main()
{
    int n;
    cin >> n;
    while(n--)
    {
        int x;
        cin >> x;
        
        int res = 0;
        while(x) x -= lowbit(x), res++;
    
        cout << res << ' ';
    }
    return 0;
}

8.离散化

假设有一串极大的数据，我们对这串数据a[i]进行离散化，其中a[i]中可能会有重复的元素，首先就是处理去重的问题，然后再进行一一映射。

vector<int>alls;//存储所有有待离散化的值
sort(alls.begin(), alls.end());//将所有值排序
alls.erase(unique(alls.begin(), alls.end()), alls.end());//去重
​
//二分法求出x对应的离散化的值
int find(int x)
{
    int l = 0, r = alls.size() - 1;
    while(l < r)
    {
        int mid = l + r >> 1;
        if(alls[mid] >= x) r = mid;
        else l = mid + 1;
    }
    return r + 1;
}

例题：区间和

假设有一个无限长的数轴，数轴上的每个坐标上的数都是0。

现在，我们首先进行n次操作，每次操作将某一位置x上的数+c

接下来，进行m次询问，每次询问包含两个整数l和r，你需要求出区间l和r之间所有数的和。

#include<iostream>
#include<vector>
#include<algorithm>
​
using namespace std;
​
typedef pair<int, int> PII; 
​
const int N = 300010;
​
int n, m;
int a[N], s[N];
​
vector<int> alls;
vector<PII> add,query;
​
int find(int x)
{
    int l = 0, r = alls.size() - 1;
    while(l < r)
    {
        int mid = l + r >> 1;
        if(alls[mid] >= x) r = mid;
        else l = mid + 1;
    }
    return r + 1;
}
​
int main()
{
    cin >> n >> m;
    for(int i = 0;i < n; i++)
    {
        int x, c;
        cin >> x >> c;
        add.push_back({x, c});
        
        alls.push_back(x);
    }
    
    for(int i = 0;i < m; i++)
    {
        int l, r;
        cin >> l >> r;
        query.push_back({l, r});
        
        alls.push_back(l);
        alls.push_back(r);
    }
    
    //去重
    sort(alls.begin(), alls.end());
    alls.erase(unique(alls.begin(), alls.end()), alls.end());
    
    for(auto item:add)
    {
        int x = find(item.first);
        a[x] += item.second;
    }
    
    //预处理前缀和
    for(int i = 1;i <= alls.size(); i++)
    {
        s[i] = s[i - 1] + a[i];
    }
    
    //处理询问
    for(auto item:query)
    {
        int l = find(item.first), r = find(item.second);
        cout << s[r] - s[l-1] << endl;
    }
    
    return 0;
}

8.1.unique函数实现

vector<int>::iterator unique(vector<int> &a)
{
    int  j = 0;
    for(int i = 0;i < a.size(); i++)
    {
        if(!a || a[i] != a[i - 1])
            a[j++] = a[i];
    }
    //a[0]~a[j-1]所有的数都是不同的
    return a.begin() + j;
}

排完序的内容中，数要么就是第一个，要么就是a[i] ≠a[i - 1]，Java和python方向是没有unique函数的，如果要写的话，就是做一个这样的迭代器。

9.区间合并

假设有大量区间，有的区间之间有重叠的部分，我们要将有交集的区间进行合并。

  1. 按区间左端点排序

  2. 扫描整个区间，将所有可能有交点的区间进行合并

#include<iostream>
#include<vector>
#include<algorithm>
​
using namespace std;
​
typedef pair<int, int> PII;
​
const int N = 100010;
​
int n;
vector<PII> segs;
​
void merge(vector<PII> &segs)
{
    vector<PII> res;
    
    sort(segs.begin(), segs.end());
    
    int st = -2e9, ed = -2e9;
    for(auto seg : segs)
    {
        if(ed < seg.first)
        {
            if(st != - 2e9) res.push_back({st, ed});
            st = seg.first, ed = seg.second;
        }
        else ed = max(ed, seg.second);
    }
    
    if(st != -2e9) res.push_back({st, ed});
    
    segs = res;
}
​
int main()
{
    cin >> n;
    
    for(int i = 0;i < n; i++)
    {
        int l ,r;
        cin >> l >> r;
        segs.push_back({l,r});
    }
    
    merge(segs);
    
    cout << segs.size() << endl;
    
    return 0;
}

 

 

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/737230.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

vue 运行时正常，打包却报错

vue 运行时正常，打包却报错

解决方法&#xff1a;删除vue-cli 自带的压缩 plugin&#xff1a;OptimizeCssnanoPlugin 具体操作&#xff1a;找到vue.config.再添加如下删除配置
阅读更多...
万万没想到！！号称国内Java八股文天花板（典藏版）首次开源

万万没想到！！号称国内Java八股文天花板（典藏版）首次开源

应届毕业生的第一份工作干多久跳槽比较合适&#xff1f; 都说现在应届毕业生找工作跳槽频繁&#xff0c;而所有用人单位都希望招揽的人才能一直在公司里干下去&#xff0c;但是人各有志&#xff0c;作为劳动者的应届毕业生有自主选择职业的权利&#xff0c;这就造成很多应届生…
阅读更多...
今天分享：智能ai绘画软件哪个好

今天分享：智能ai绘画软件哪个好

在一个遥远的未来&#xff0c;艺术界经历了一场革命性的变革。艺术家们不再依赖传统的画笔和颜料&#xff0c;而是转向了ai绘画工具&#xff0c;这是一种集人工智能和创造力于一身的技术。在这个世界中&#xff0c;我有幸遇到了一个与众不同的艺术家&#xff0c;他的名字叫亚历…
阅读更多...
Hubspot为什么这么牛？国内有哪些类似软件

Hubspot为什么这么牛？国内有哪些类似软件

国外CRM圈内&#xff0c;除了大佬Salesforce外&#xff0c;还有HubSpot、Oracle、SAP等知名CRM公司。其中&#xff0c;HubSpot在国外2023年最佳CRM软件排行榜中名列第四&#xff0c;在最佳免费CRM软件排行榜中名列第二&#xff0c;我们先来看下它到底有多优秀&#xff0c;然后再…
阅读更多...
Deffie-Hellman 算法

Deffie-Hellman 算法

Deffie-Hellman 算法简介 Deffie-Hellman(简称 DH) 密钥交换是最早的密钥交换算法之一&#xff0c;它使得通信的双方能在非安全的信道中安全的交换密钥&#xff0c;用于加密后续的通信消息。 Whitfield Diffie 和 Martin Hellman 于 1976 提出该算法&#xff0c;之后被应用于安…
阅读更多...
指令周期的数据流

指令周期的数据流

5.2 指令周期的数据流 指令周期 机器周期/CPU周期 CPU时钟周期/节拍 取指周期 间址周期 执行周期 中断周期 标志触发器FE IND EX INT 数据流 取指周期 根据PC中的内容取出指令代码并存放在IR中 间址周…
阅读更多...
Acrelcloud-9500 智能电瓶车充电桩收费云平台

Acrelcloud-9500 智能电瓶车充电桩收费云平台

1. 概述 电动车火灾事故频频发生&#xff0c;毫不起眼的电动车屡次引发夺命大火&#xff0c;电动车已然成为火灾“重灾区”。为预防和遏制电动自行车火灾事故发生&#xff0c;三令五申各种政策&#xff0c;为此安委会曾出台《电动自行车集中停放和充电治理方案》。 大部分充电过…
阅读更多...
Linux - 进阶 NFS 服务器 工作原理，安装，主文件分析

Linux - 进阶 NFS 服务器 工作原理，安装，主文件分析

NFS工作原理 : 示例图 &#xff1a; 我们在上篇文章也讲过&#xff0c; 要实现 NFS 服务的搭建&#xff0c;最起码得 两个 服务 &#xff08; NFS 服务&#xff0c;RPC 服务&#xff09; 涉及 三方 &#xff1a; 服务端 &#xff08; 房源 &#xff09; 客户端 &…
阅读更多...
如何将mov转换成mp4？这篇文章教会你如何转换

如何将mov转换成mp4？这篇文章教会你如何转换

MP4格式是一种通用的视频格式&#xff0c;几乎所有的播放器都能够支持它&#xff0c;包括电视、智能手机、平板电脑等等。而mov格式则主要被苹果设备所使用&#xff0c;其他设备可能会出现无法播放的情况。由于MP4格式的广泛兼容性&#xff0c;可以更方便地分享视频给其他人观看…
阅读更多...
linux入门之进程控制（下）进程程序替换，shell运行原理，手写一个mini-shell

linux入门之进程控制（下）进程程序替换，shell运行原理，手写一个mini-shell

文章目录 一、进程程序替换 1.替换原理 2.替换函数 3.函数解释 4.命名理解 二、手写一个mini Shell 一、进程程序替换 创建子进程的目的就是为了让子进程执行特定的任务&#xff0c;比如&#xff1a;1.让子进程执行父进程的一部分代码&#xff1b;2.让子进程指向一个全新的程序…
阅读更多...
java项目之高校二手交易平台(ssm+mysql+jsp)

java项目之高校二手交易平台(ssm+mysql+jsp)

风定落花生&#xff0c;歌声逐流水&#xff0c;大家好我是风歌&#xff0c;混迹在java圈的辛苦码农。今天要和大家聊的是一款基于ssm的高校二手交易平台。技术交流和部署相关看文章末尾&#xff01; 开发环境&#xff1a; 后端&#xff1a; 开发语言&#xff1a;Java 框架…
阅读更多...
建站教程：阿里云轻量应用服务器搭建网站流程

建站教程：阿里云轻量应用服务器搭建网站流程

阿里云轻量应用服务器怎么使用&#xff1f;阿里云百科分享轻量应用服务器从选配、配置建站环境、轻量服务器应用服务器远程连接、开端口到网站上线全流程&#xff1a; 阿里云轻量应用服务器使用教程 轻量应用服务器很火爆因为成本足够低&#xff0c;阿里云2核2G3M带宽轻量服务…
阅读更多...
基于Linux下的C语言项目实战--本地账号管理系统

基于Linux下的C语言项目实战--本地账号管理系统

C语言开发项目实战&#xff1a; C语言是一门通用计算机编程语言&#xff0c;广泛应用于底层开发。C语言的设计目标是提供一种能以简易的方式编译、处理低级存储器、产生少量的机器码以及不需要任何运行环境支持便能运行的编程语言。尽管C语言提供了许多低级处理的功能&#xff…
阅读更多...
SpringBoot中间件—封装超时熔断器

SpringBoot中间件—封装超时熔断器

需求背景 如果一个服务中有很多涉及需要服务间熔断的地方&#xff0c;就会出现N多下述代码&#xff1a; 1.N个fegnClient接口 FeignClient(name "hello-world-service", fallback HelloWorldFallback.class) public interface HelloWorldService {GetMapping(&q…
阅读更多...
U盘写保护怎样去掉？分享3种简单方法！

U盘写保护怎样去掉？分享3种简单方法！

不知道为什么我的u盘突然就显示被写保护了呢&#xff0c;大家有没有遇到过类似的情况呀&#xff1f;有什么比较好的解决方法可以推荐一下吗&#xff1f; 很多朋友可能对u盘写保护没有什么概念&#xff0c;实际上&#xff0c;u盘写保护可能会阻止我们对其中的文件进行修改或者添…
阅读更多...
含生僻字中文校验方式优化

含生僻字中文校验方式优化

项目姓名校验原本一直是通过utf8正则进行校验&#xff0c;但近期出现的客户生僻字包含双码字&#xff0c;原有校验方式无法实现。需要修改扩大校验范围。 知识点回顾&#xff1a; Unicode是Unicode Standard&#xff08;Unicode标准&#xff09;的简写&#xff1b;Unicode为每…
阅读更多...
HNU-操作系统OS-学习感悟

HNU-操作系统OS-学习感悟

初次接触如此底层的计算机基础课程&#xff0c;我还是很不适应的。 教材用的这本书&#xff0c;实验用的清华大学的ucore实验 好在应试水平没有丢。最后总评94/100。 下面仅从应试角度谈一谈学习的理解 总领 HNU的OS课程平时分给的比较模糊&#xff0c;大致由 作业实验验…
阅读更多...
先导式比例溢流阀放大器

先导式比例溢流阀放大器

EDBW10PL350XY/224、EDBW20PL210XY/724、EDBW30PL105XY/224、EDBW10PL055XY/224先导式比例溢流阀&#xff0c;板式安装&#xff0c;由主阀芯和先导级阀beuec比例放大器组成:先导级阀为比例溢流阀&#xff0c;主阀阅芯可独立调节压力作为安全限压压力&#xff0c;比例先导阀压力…
阅读更多...
selenium怎么使用代理IP

selenium怎么使用代理IP

什么是selenium Selenium 是一个自动化测试框架&#xff0c;用于测试 Web 应用程序的功能性。它支持多个编程语言&#xff08;如Java&#xff0c;Python&#xff0c;C#等&#xff09;并且可以在操作系统和不同浏览器上运行测试。Selenium 可以模拟用户在浏览器中的操作&#x…
阅读更多...
PC端实现滚动分页懒加载

PC端实现滚动分页懒加载

思路 监听列表元素的滚动事件&#xff0c;滚动到底部的时候&#xff0c;加载下一页的数据监听数据加载&#xff0c;判断是否已全部加载结束 实现 监听滚动事件 为列表元素 listBox 绑定 scroll 事件进行监听 <div class"listBox" scroll"watchScroll&qu…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023