【Matlab】智能优化算法_麻雀搜索算法SSA
- 1.背景介绍
- 2.数学模型
- 3.文件结构
- 4.伪代码
- 5.详细代码及注释
- 5.1 Get_Functions_details.m
- 5.2 main.m
- 5.3 SSA.m
- 6.运行结果
- 7.参考文献
1.背景介绍
麻雀通常是群居的鸟类,有很多种类。它们分布在世界的大部分地区,喜欢生活在人类生活的地方。此外,它们是杂食性鸟类,主要以谷物或杂草的种子为食。众所周知,麻雀是常见的留鸟。与其他许多小鸟相比,麻雀有很强的智慧,有很强的记忆力。请注意,有两种不同类型的圈养家雀,都是生产者和寻食者。生产者积极寻找食物来源,而蹭食者则通过生产者获得食物。此外,证据显示,鸟类通常灵活地使用行为策略,在生产和蹭食之间切换。也可以说,为了寻找他们的食物,麻雀通常使用生产者和搜寻者的策略。
研究表明,个体监视群体中其他人的行为。同时,鸟群中的攻击者,想提高自己的捕食率,就会用高摄入量的同伴来竞争食物资源。此外,当麻雀选择不同的觅食策略时,个体的能量储备可能起到重要的作用,能量储备低的麻雀会更多地蹭吃蹭喝。值得一提的是,位于种群外围的鸟类,更有可能受到捕食者的攻击,并不断尝试获得更好的位置。请注意,位于中心的动物,可能会向它们的邻居靠近,以减少它们的危险领域。我们还知道,所有的麻雀都表现出对一切事物好奇的自然本能,同时它们也总是保持着警惕。例如,当一只鸟确实检测到捕食者时,一个或多个个体发出一声鸣叫,整个群体就会飞走。
2.数学模型
麻雀搜索算法。为了简单起见,我们将麻雀的以下行为理想化,并制定了相应的规则。
- 生产者通常有高水平的能量储备,并为所有蹭吃蹭喝的人提供觅食区或方向。它负责识别可以找到丰富食物来源的区域。能量储备的水平取决于对个体的健身价值的评估。
- 一旦麻雀发现捕食者,个体就开始鸣叫作为报警信号。当报警值大于安全阈值时,生产者需要带领所有的蹭食者到安全区域。
- 每只麻雀只要寻找更好的食物来源,就能成为生产者,但整个种群中生产者和蹭食者的比例是不变的。
- 具有较高能量的麻雀会被当作生产者。几个饥饿的蹭食者更有可能飞到其他地方寻找食物,以获得更多的能量。
- 蹭食者跟随能提供最佳食物的生产者去寻找食物。同时,一些蹭食者可能会不断地监视生产者并争夺食物,以增加自己的捕食率。
- 当意识到有危险时,处于群体边缘的麻雀迅速向安全区域移动,以获得更好的位置,而处于群体中间的麻雀则随机行走,以接近其他人。
在模拟实验中,我们需要使用虚拟麻雀来寻找食物。麻雀的位置可以用以下矩阵表示:

其中n是麻雀的数量,d表示要优化的变量的维度。然后,所有麻雀的适应度值可以用以下向量表示:

其中n表示麻雀的数量,FX中每行的值表示个体的适应度值。在SSA中,具有更好适应度值的生产者在搜索过程中优先获得食物。此外,因为生产者负责搜索食物和引导整个人口的流动。所以,生产者可以在比拾荒者更广泛的地方寻找食物。根据规则(1)和(2),在每次迭代过程中,生产者的位置更新如下:

其中t表示当前迭代,j=1,2。。。,d.Xt i,j表示迭代时第i个麻雀的第j维的值。itermax是迭代次数最多的常数。α∈(0,1]是一个随机数。R2(R2∈[0,1])和ST(ST∈[0.5,1.0])分别表示报警值和安全阈值。Q是服从正态分布的随机数。L表示amatrixof1×d,其中内部的每个元素都是1。
当R2<ST时,这意味着周围没有捕食者,生产者进入广泛搜索模式。如果R2≥ST,则意味着一些麻雀已经发现了捕食者,所有麻雀都需要迅速飞往其他安全区域。
至于拾荒者,他们需要执行规则(4)和(5)。如上所述,一些拾荒者更频繁地监视生产者。一旦他们发现生产者找到了好的食物,他们就会立即离开目前的位置去争夺食物。如果他们赢了,他们可以立即得到生产者的食物,否则他们将继续执行规则(5)。搜寻者的位置更新公式如下所述:

其中XP是生产者占据的最佳位置。Xworst表示当前全球最差位置。A代表一个1×d的矩阵,里面的每个元素都被随机分配为1或-1,A+=AT(AAT )-1。当i>n/2时,表明健身值较差的第1个蹭饭的人最有可能挨饿。
在模拟实验中,我们假设这些意识到危险的麻雀占总种群的10%到20%。这些麻雀的初始位置是在种群中随机产生的。根据规则(6),数学模型可以表达如下:

其中Xbest是当前的全局最优位置。β,作为步长控制参数,是一个均值为0,方差为1的正态分布的随机数。 K∈[-1, 1]是一个随机数。这里fi是当前麻雀的适配值。fg和fw分别是当前全球最佳和最差的适配值。ε是最小的常数,以避免零除法错误。
为了简单起见,当fi > fg时,表示麻雀处于群体的边缘。Xbest代表种群中心的位置,在其周围是安全的。fi = fg表明处于种群中间的麻雀意识到了危险,需要向其他麻雀靠近。K表示麻雀移动的方向,也是步长的控制系数。
3.文件结构

Get_Functions_details.m % 基准的全部信息和实现
main.m % 主函数
SSA.m % 麻雀搜索算法
4.伪代码

5.详细代码及注释
5.1 Get_Functions_details.m
function [lb,ub,dim,fobj] = Get_Functions_details(F)
switch F
case 'F1'
fobj = @F1;
lb=-100;
ub=100;
dim=30;
case 'F2'
fobj = @F2;
lb=-10;
ub=10;
dim=30;
case 'F3'
fobj = @F3;
lb=-100;
ub=100;
dim=30;
case 'F4'
fobj = @F4;
lb=-100;
ub=100;
dim=30;
case 'F5'
fobj = @F5;
lb=-30;
ub=30;
dim=30;
case 'F6'
fobj = @F6;
lb=-100;
ub=100;
dim=30;
case 'F7'
fobj = @F7;
lb=-1.28;
ub=1.28;
dim=30;
case 'F8'
fobj = @F8;
lb=-500;
ub=500;
dim=30;
case 'F9'
fobj = @F9;
lb=-5.12;
ub=5.12;
dim=30;
case 'F10'
fobj = @F10;
lb=-32;
ub=32;
dim=30;
case 'F11'
fobj = @F11;
lb=-600;
ub=600;
dim=30;
case 'F12'
fobj = @F12;
lb=-50;
ub=50;
dim=30;
case 'F13'
fobj = @F13;
lb=-50;
ub=50;
dim=30;
case 'F14'
fobj = @F14;
lb=-65.536;
ub=65.536;
dim=2;
case 'F15'
fobj = @F15;
lb=-5;
ub=5;
dim=4;
case 'F16'
fobj = @F16;
lb=-5;
ub=5;
dim=2;
case 'F17'
fobj = @F17;
lb=[-5,0];
ub=[10,15];
dim=2;
case 'F18'
fobj = @F18;
lb=-2;
ub=2;
dim=2;
case 'F19'
fobj = @F19;
lb=0;
ub=1;
dim=3;
case 'F20'
fobj = @F20;
lb=0;
ub=1;
dim=6;
case 'F21'
fobj = @F21;
lb=0;
ub=10;
dim=4;
case 'F22'
fobj = @F22;
lb=0;
ub=10;
dim=4;
case 'F23'
fobj = @F23;
lb=0;
ub=10;
dim=4;
end
end
% F1
function o = F1(x)
o=sum(x.^2);
end
% F2
function o = F2(x)
o=sum(abs(x))+prod(abs(x));
end
% F3
function o = F3(x)
dim=size(x,2);
o=0;
for i=1:dim
o=o+sum(x(1:i))^2;
end
end
% F4
function o = F4(x)
o=max(abs(x));
end
% F5
function o = F5(x)
dim=size(x,2);
o=sum(100*(x(2:dim)-(x(1:dim-1).^2)).^2+(x(1:dim-1)-1).^2);
end
% F6
function o = F6(x)
o=sum(abs((x+.5)).^2);
end
% F7
function o = F7(x)
dim=size(x,2);
o=sum([1:dim].*(x.^4))+rand;
end
% F8
function o = F8(x)
o=sum(-x.*sin(sqrt(abs(x))));
end
% F9
function o = F9(x)
dim=size(x,2);
o=sum(x.^2-10*cos(2*pi.*x))+10*dim;
end
% F10
function o = F10(x)
dim=size(x,2);
o=-20*exp(-.2*sqrt(sum(x.^2)/dim))-exp(sum(cos(2*pi.*x))/dim)+20+exp(1);
end
% F11
function o = F11(x)
dim=size(x,2);
o=sum(x.^2)/4000-prod(cos(x./sqrt([1:dim])))+1;
end
% F12
function o = F12(x)
dim=size(x,2);
o=(pi/dim)*(10*((sin(pi*(1+(x(1)+1)/4)))^2)+sum((((x(1:dim-1)+1)./4).^2).*...
(1+10.*((sin(pi.*(1+(x(2:dim)+1)./4)))).^2))+((x(dim)+1)/4)^2)+sum(Ufun(x,10,100,4));
end
% F13
function o = F13(x)
dim=size(x,2);
o=.1*((sin(3*pi*x(1)))^2+sum((x(1:dim-1)-1).^2.*(1+(sin(3.*pi.*x(2:dim))).^2))+...
((x(dim)-1)^2)*(1+(sin(2*pi*x(dim)))^2))+sum(Ufun(x,5,100,4));
end
% F14
function o = F14(x)
aS=[-32 -16 0 16 32 -32 -16 0 16 32 -32 -16 0 16 32 -32 -16 0 16 32 -32 -16 0 16 32;,...
-32 -32 -32 -32 -32 -16 -16 -16 -16 -16 0 0 0 0 0 16 16 16 16 16 32 32 32 32 32];
for j=1:25
bS(j)=sum((x'-aS(:,j)).^6);
end
o=(1/500+sum(1./([1:25]+bS))).^(-1);
end
% F15
function o = F15(x)
aK=[.1957 .1947 .1735 .16 .0844 .0627 .0456 .0342 .0323 .0235 .0246];
bK=[.25 .5 1 2 4 6 8 10 12 14 16];bK=1./bK;
o=sum((aK-((x(1).*(bK.^2+x(2).*bK))./(bK.^2+x(3).*bK+x(4)))).^2);
end
% F16
function o = F16(x)
o=4*(x(1)^2)-2.1*(x(1)^4)+(x(1)^6)/3+x(1)*x(2)-4*(x(2)^2)+4*(x(2)^4);
end
% F17
function o = F17(x)
o=(x(2)-(x(1)^2)*5.1/(4*(pi^2))+5/pi*x(1)-6)^2+10*(1-1/(8*pi))*cos(x(1))+10;
end
% F18
function o = F18(x)
o=(1+(x(1)+x(2)+1)^2*(19-14*x(1)+3*(x(1)^2)-14*x(2)+6*x(1)*x(2)+3*x(2)^2))*...
(30+(2*x(1)-3*x(2))^2*(18-32*x(1)+12*(x(1)^2)+48*x(2)-36*x(1)*x(2)+27*(x(2)^2)));
end
% F19
function o = F19(x)
aH=[3 10 30;.1 10 35;3 10 30;.1 10 35];cH=[1 1.2 3 3.2];
pH=[.3689 .117 .2673;.4699 .4387 .747;.1091 .8732 .5547;.03815 .5743 .8828];
o=0;
for i=1:4
o=o-cH(i)*exp(-(sum(aH(i,:).*((x-pH(i,:)).^2))));
end
end
% F20
function o = F20(x)
aH=[10 3 17 3.5 1.7 8;.05 10 17 .1 8 14;3 3.5 1.7 10 17 8;17 8 .05 10 .1 14];
cH=[1 1.2 3 3.2];
pH=[.1312 .1696 .5569 .0124 .8283 .5886;.2329 .4135 .8307 .3736 .1004 .9991;...
.2348 .1415 .3522 .2883 .3047 .6650;.4047 .8828 .8732 .5743 .1091 .0381];
o=0;
for i=1:4
o=o-cH(i)*exp(-(sum(aH(i,:).*((x-pH(i,:)).^2))));
end
end
% F21
function o = F21(x)
aSH=[4 4 4 4;1 1 1 1;8 8 8 8;6 6 6 6;3 7 3 7;2 9 2 9;5 5 3 3;8 1 8 1;6 2 6 2;7 3.6 7 3.6];
cSH=[.1 .2 .2 .4 .4 .6 .3 .7 .5 .5];
o=0;
for i=1:5
o=o-((x-aSH(i,:))*(x-aSH(i,:))'+cSH(i))^(-1);
end
end
% F22
function o = F22(x)
aSH=[4 4 4 4;1 1 1 1;8 8 8 8;6 6 6 6;3 7 3 7;2 9 2 9;5 5 3 3;8 1 8 1;6 2 6 2;7 3.6 7 3.6];
cSH=[.1 .2 .2 .4 .4 .6 .3 .7 .5 .5];
o=0;
for i=1:7
o=o-((x-aSH(i,:))*(x-aSH(i,:))'+cSH(i))^(-1);
end
end
% F23
function o = F23(x)
aSH=[4 4 4 4;1 1 1 1;8 8 8 8;6 6 6 6;3 7 3 7;2 9 2 9;5 5 3 3;8 1 8 1;6 2 6 2;7 3.6 7 3.6];
cSH=[.1 .2 .2 .4 .4 .6 .3 .7 .5 .5];
o=0;
for i=1:10
o=o-((x-aSH(i,:))*(x-aSH(i,:))'+cSH(i))^(-1);
end
end
function o=Ufun(x,a,k,m)
o=k.*((x-a).^m).*(x>a)+k.*((-x-a).^m).*(x<(-a));
end
5.2 main.m
clc
clear
close all
SearchAgents_no=100; % Number of search agents
Function_name='F15'; % Name of the test function that can be from F1 to F23 (Table 1,2,3 in the paper)
Max_iteration=1000; % Maximum numbef of iterations
% Load details of the selected benchmark function
[lb,ub,dim,fobj]=Get_Functions_details(Function_name);
[fMin,bestX,SSA_curve]=SSA(SearchAgents_no,Max_iteration,lb,ub,dim,fobj);
%Draw objective space
semilogy(SSA_curve,'Color','g')
axis ([0 1000 0 1 ])
title('Objective space')
xlabel('Iteration');
ylabel('Best score obtained so far');
%axis tight
grid on
box on
legend('SSA')
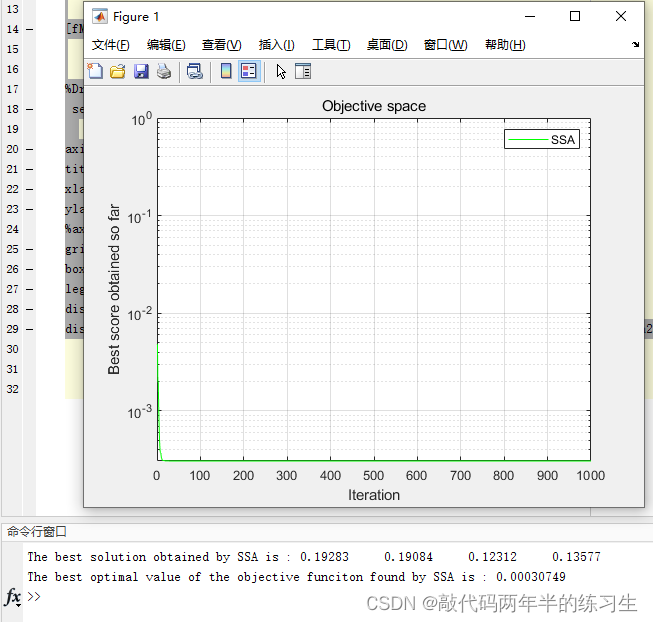
display(['The best solution obtained by SSA is : ', num2str(bestX)]);
display(['The best optimal value of the objective funciton found by SSA is : ', num2str(fMin)]);
5.3 SSA.m
function [fMin , bestX,Convergence_curve ] = SSA(pop, M,c,d,dim,fobj )
P_percent = 0.2; % The population size of producers accounts for "P_percent" percent of the total population size
pNum = round( pop * P_percent ); % The population size of the producers
lb= c.*ones( 1,dim ); % Lower limit/bounds/ a vector
ub= d.*ones( 1,dim ); % Upper limit/bounds/ a vector
%Initialization
for i = 1 : pop
x( i, : ) = lb + (ub - lb) .* rand( 1, dim );
fit( i ) = fobj( x( i, : ) ) ;
end
pFit = fit;
pX = x; % The individual's best position corresponding to the pFit
[ fMin, bestI ] = min( fit ); % fMin denotes the global optimum fitness value
bestX = x( bestI, : ); % bestX denotes the global optimum position corresponding to fMin
% Start updating the solutions.
for t = 1 : M
[ ans, sortIndex ] = sort( pFit );% Sort.
[fmax,B]=max( pFit );
worse= x(B,:);
r2=rand(1);
if(r2<0.8)
for i = 1 : pNum % Equation (3)
r1=rand(1);
x( sortIndex( i ), : ) = pX( sortIndex( i ), : )*exp(-(i)/(r1*M));
x( sortIndex( i ), : ) = Bounds( x( sortIndex( i ), : ), lb, ub );
fit( sortIndex( i ) ) = fobj( x( sortIndex( i ), : ) );
end
else
for i = 1 : pNum
x( sortIndex( i ), : ) = pX( sortIndex( i ), : )+randn(1)*ones(1,dim);
x( sortIndex( i ), : ) = Bounds( x( sortIndex( i ), : ), lb, ub );
fit( sortIndex( i ) ) = fobj( x( sortIndex( i ), : ) );
end
end
[ fMMin, bestII ] = min( fit );
bestXX = x( bestII, : );
for i = ( pNum + 1 ) : pop % Equation (4)
A=floor(rand(1,dim)*2)*2-1;
if( i>(pop/2))
x( sortIndex(i ), : )=randn(1)*exp((worse-pX( sortIndex( i ), : ))/(i)^2);
else
x( sortIndex( i ), : )=bestXX+(abs(( pX( sortIndex( i ), : )-bestXX)))*(A'*(A*A')^(-1))*ones(1,dim);
end
x( sortIndex( i ), : ) = Bounds( x( sortIndex( i ), : ), lb, ub );
fit( sortIndex( i ) ) = fobj( x( sortIndex( i ), : ) );
end
c=randperm(numel(sortIndex));
b=sortIndex(c(1:20));
for j = 1 : length(b) % Equation (5)
if( pFit( sortIndex( b(j) ) )>(fMin) )
x( sortIndex( b(j) ), : )=bestX+(randn(1,dim)).*(abs(( pX( sortIndex( b(j) ), : ) -bestX)));
else
x( sortIndex( b(j) ), : ) =pX( sortIndex( b(j) ), : )+(2*rand(1)-1)*(abs(pX( sortIndex( b(j) ), : )-worse))/ ( pFit( sortIndex( b(j) ) )-fmax+1e-50);
end
x( sortIndex(b(j) ), : ) = Bounds( x( sortIndex(b(j) ), : ), lb, ub );
fit( sortIndex( b(j) ) ) = fobj( x( sortIndex( b(j) ), : ) );
end
for i = 1 : pop
if ( fit( i ) < pFit( i ) )
pFit( i ) = fit( i );
pX( i, : ) = x( i, : );
end
if( pFit( i ) < fMin )
fMin= pFit( i );
bestX = pX( i, : );
end
end
Convergence_curve(t)=fMin;
end
% Application of simple limits/bounds
function s = Bounds( s, Lb, Ub)
% Apply the lower bound vector
temp = s;
I = temp < Lb;
temp(I) = Lb(I);
% Apply the upper bound vector
J = temp > Ub;
temp(J) = Ub(J);
% Update this new move
s = temp;
%---------------------------------------------------------------------------------------------------------------------------
6.运行结果
7.参考文献
[1]Xue J,Shen B. A novel swarm intelligence optimization approach: sparrow search algorithm[J]. Systems Science & Control Engineering,2020,8(1).