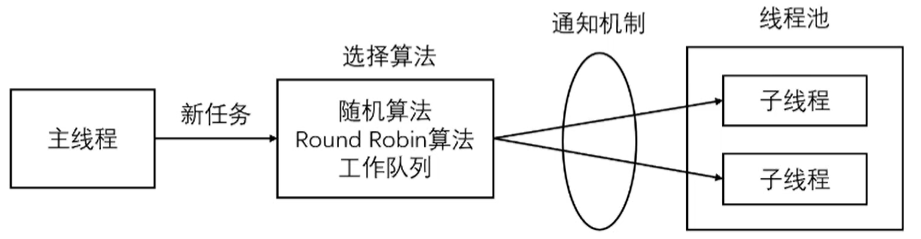
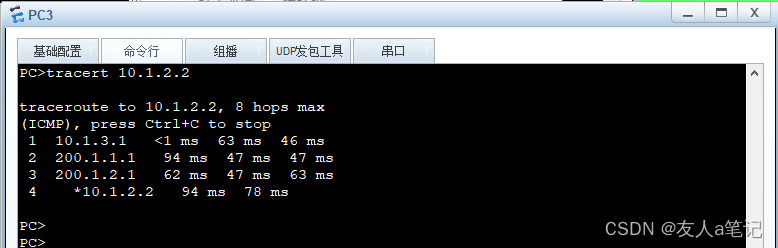
分解本质矩阵的过程遵循以下步骤：

1. 使用奇异值分解（SVD）计算本质矩阵E的分解。SVD分解是一种将矩阵分解为三个矩阵的乘积的方法，它的形式为 E = UΣV^T，其中U和V是正交矩阵，Σ是对角矩阵。此步骤的结果存储在u、w和vt中。

2. 把U矩阵的第三列复制到t，并进行归一化。t代表相机的平移向量。

3. 定义W矩阵。在某些情况下，W也被称为"旋转矩阵"，它是由本质矩阵E的属性决定的。

4. 计算两个可能的旋转矩阵R1和R2。这两个矩阵代表相机的旋转。

5. 检查R1和R2的行列式。如果行列式为负，则将对应的旋转矩阵取反。因为在计算机视觉中，我们通常希望旋转矩阵具有正的行列式，这意味着它们代表了一个右手坐标系的旋转。

根据本质矩阵E，计算两个可能的旋转矩阵和一个平移向量。结果用于相机姿态估计。