一、实验目的
1:掌握加减法器工作原理。
2:能够设计出一个n位加减法器。
3:熟悉Logisim软件使用。
二、实验环境
(1)Logisim 2.7.1
(2)Microsoft Windows 10
三、实验内容
1:设计一个1位的全加法器FA
(1)利用与门、或门、异或门等组件,设计加法电路。
2:设计一个用4个FA4构成一个4位的加减法器
(1)可以在引脚输出结果,并显示在LED上。输入采用手动设置引脚。
(2)将减法器的手动输入,改为计数器C1,C2的4位输出值,并显示在LED上。
四、实验步骤
实验1:1位全加器
(1)实验设计分析
首先,通过逻辑抽象为真值表。通过分析全加器的逻辑功能后,我们容易得到全加器有三个输入端,即加数、被加数和低一级的进位,同时其有两个输出端,即当前位置的进位和当前位置的加法运算结果。
令加数为A,被加数为B,低一级的进位为Ci,当前位置的加法运算结果为S,当前位置的进位为Co,我们可以得到五个变量的真值表,结果如下所示:
| A | B | Ci | S | Co |
| 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 | 0 |
| 0 | 1 | 0 | 1 | 0 |
| 0 | 1 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 | 0 |
| 1 | 0 | 1 | 0 | 1 |
| 1 | 1 | 0 | 0 | 1 |
| 1 | 1 | 1 | 1 | 1 |
其次,通过真值表写表达式。通过结果列S和Co,我们可以得到S和Co的原始逻辑表达式和化简逻辑表达式(通过卡诺图)为:
S = A’B’Ci + A’BCi’ + AB’Ci’ + ABCi = A⊕![]() B⊕
B⊕![]() Ci
Ci
Co = A’BCi + AB’Ci + ABCi’ + ABCi = AB + ACi + BCi
因此,在电路图的设计中,S端的处理应该将A和B先通过一次异或门得到A异或B,将A异或B的结果和Ci再通过一次异或门得到A异或B异或Ci。同时,Co端的处理应该将A和B、A和Ci、B和Ci先通过一次与门得到AB、ACi、BCi,再将AB和ACi和BCi再通过一次或门得到AB + ACi + BCi。
综上所述,本实验可以利用与门、或门、异或门组件,设计一套完整的加法电路。
(2)实验连线图

最终实验的模拟电路图存在于0-1.circ中的add组件,电路图如下所示:
(3)实验结果图
基于(1)中的真值表,我们可以进行相关的模拟测验,最终的测验结果及其截图如下所示:
| 输入测试ABCi | 实验结果S | 实验结果Co |
| 000 | 0 | 0 |
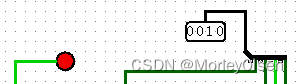
| 001 | 1 | 0 |
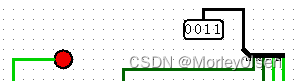
| 010 | 1 | 0 |
| 011 | 0 | 1 |
| 100 | 1 | 0 |
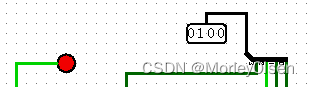
| 101 | 0 | 1 |
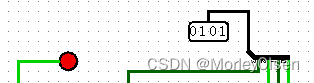
| 110 | 0 | 1 |
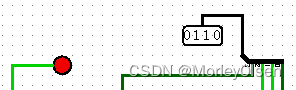
| 111 | 1 | 1 |
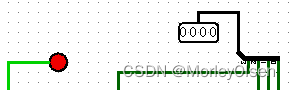
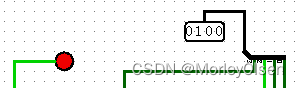
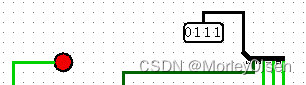
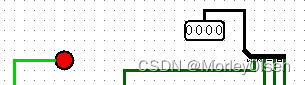
000:
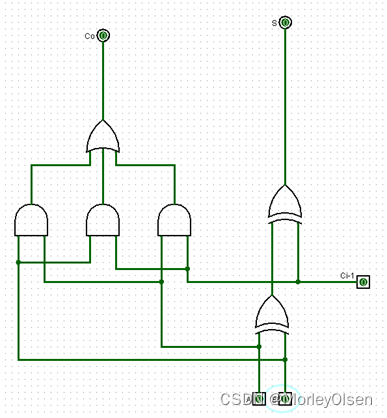
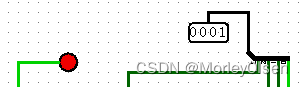
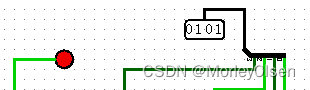
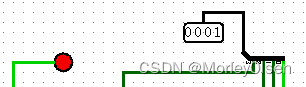
001:
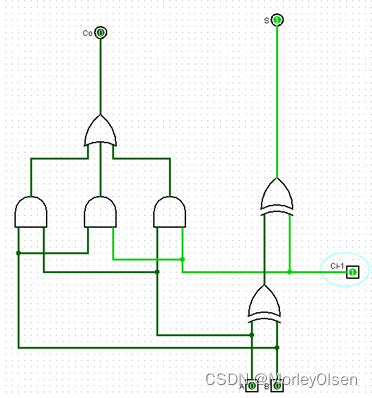
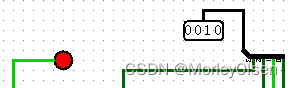
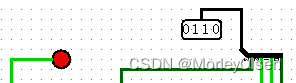
010:
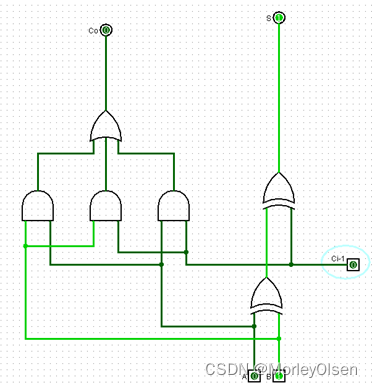
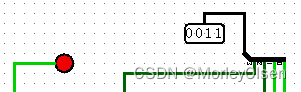
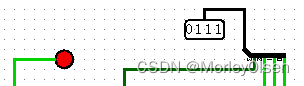
011:
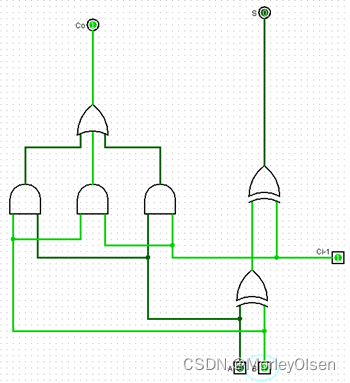
100:

101:
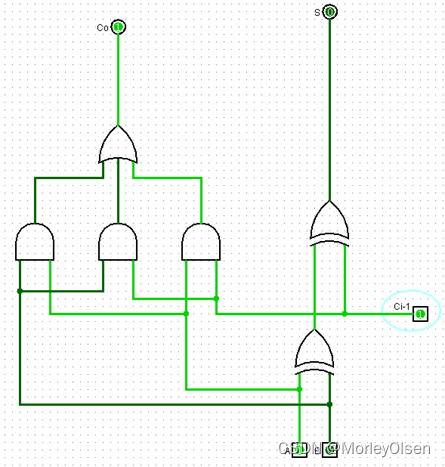
110:
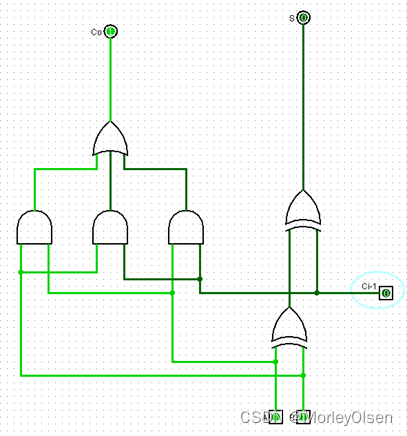
111:
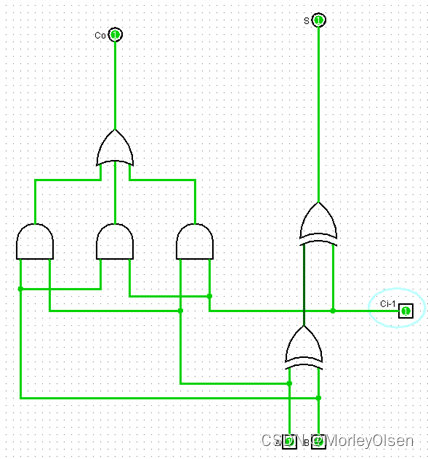
实验2:4位加减法器
(1)实验设计分析
首先,通过逻辑抽象为真值表。由于实验1已经实现了加法器的功能,因此实验2只需在加法器的基础上实现减法器的功能。通过分析全减器的逻辑功能后,我们容易得到全减器有三个输入端,即减数、被减数和高一级的借位,同时其有两个输出端,即当前位置的借位和当前位置的减法运算结果。
令被减数为A,减数为B,高一级的借位为Ci,当前位置的加减法运算结果为D,当前位置的借位为Co,我们可以得到五个变量的真值表,结果如下所示:
| Ci | A | B | D | Co |
| 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 | 1 |
| 0 | 1 | 0 | 1 | 0 |
| 0 | 1 | 1 | 0 | 0 |
| 1 | 0 | 0 | 1 | 1 |
| 1 | 0 | 1 | 0 | 1 |
| 1 | 1 | 0 | 0 | 0 |
| 1 | 1 | 1 | 1 | 1 |
其次,通过真值表写表达式。通过结果列D和Co,我们可以得到D和Co的原始逻辑表达式和化简逻辑表达式(通过卡诺图)为:
D = Ci’A’B + Ci’AB’ + CiA’B’ + CiAB = = A⊕![]() B⊕
B⊕![]() Ci
Ci
Co = Ci’A’B + CiA’B’+ CiA’B + CiAB = A’B + CiA’ + CiB
而实验1中的S和Co的表达式为:
S = A’B’Ci’ + A’BCi’ + AB’Ci’ + ABCi = A⊕![]() B⊕
B⊕![]() Ci
Ci
Co = A’BCi + AB’Ci + ABCi’ + ABCi = AB + ACi + BCi
通过对比实验1的结果我们可以发现:S的结果和D的结果完全相同,加法器Co的结果中将A取反之后与减法器中的结果完全相同。因此,在电路图的设计中,我们可以设置一个sub检测器,通过sub的值来决定运算器是做加法还是做减法。当sub=1时,运算器做减法;当sub=0时,运算器做加法。在上述分析中,当A取原本值时,运算器做加法;当A取负值时,运算器做减法。
| A | Sub | 理论的运行结果 |
| 0 | 0 | 加法,输入为0 |
| 0 | 1 | 减法,输入为1 |
| 1 | 0 | 加法,输入为1 |
| 1 | 1 | 减法,输入为0 |
通过上面的真值表,我们发现可以将A和sub取异或值,输入到运算器中的A端,即将sub和A通过异或门后的结果作为输入。通过这种方法,我们可以得到完整的一位加减法器,且减法运算时采用了补码。
由于实验2需要得到4位加减法器,因此需要对4个1位加减法器进行串联连接,将当前运算器的Ci端连接上一位运算器的Co端,并将当前运算器的Co端连接下一位运算器的Ci端,实现进位的连续性。
综上所述,本实验可以利用实验1的add集成、异或门组件,设计一套完整的4位加减法电路。
(2)实验连线图
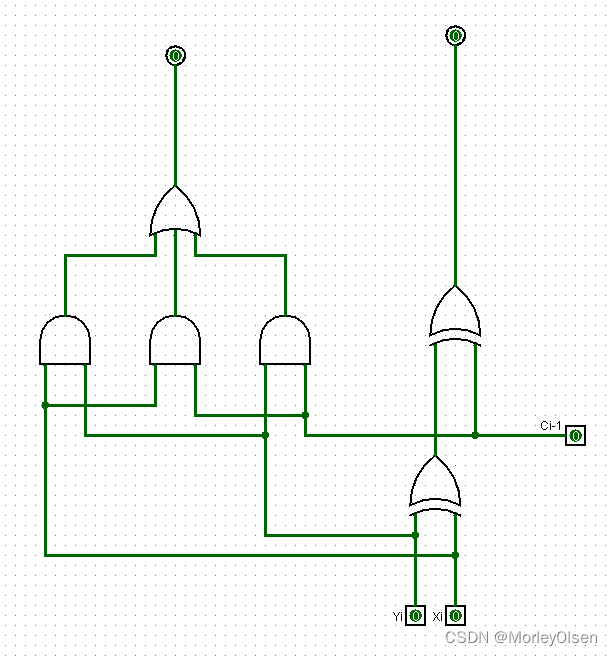
1位全加器:
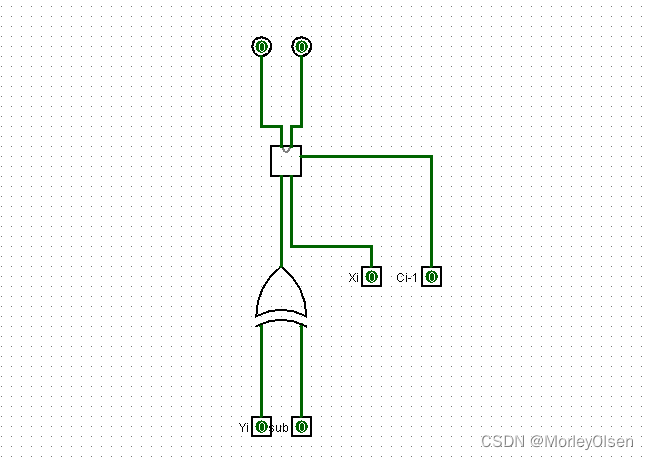
基于全加器的1位加减法器:
基于1位加减法器的4位加减法器:
手动调整X和Y的数值版本

时钟自动设定X和Y的数值,并用LED显示计算结果
(3)实验结果图
手动调整X和Y的数值版本:
基于(1)中的真值表,我们可以进行相关的模拟测验,最终的测验结果及其截图如下所示:
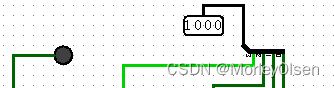
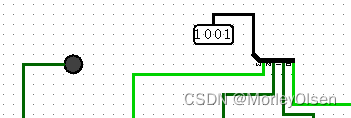
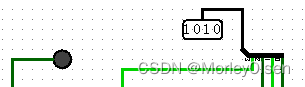
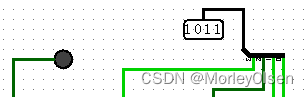
加法情况【由于Y和X同时变化时,X+Y状态较多,因此此处仅以Y为1000不变,X从0000依次变换到1111为例,列出实验的各项指标的结果】:
| 输入测试Y | 输入测试X | 实验运算结果 | 实验结果最终进位 | 实验结果截图 | |||
| 1000 | 0000 | 1000 | 0 |
| |||
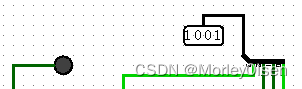
| 1000 | 0001 | 1001 | 0 |
| |||
| 1000 | 0010 | 1010 | 0 |
| |||
| 1000 | 0011 | 1011 | 0 |
| |||
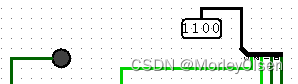
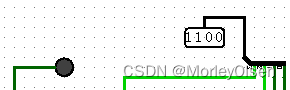
| 1000 | 0100 | 1100 | 0 |
| |||
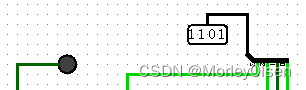
| 1000 | 0101 | 1101 | 0 |
| |||
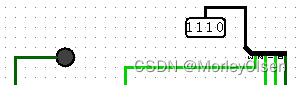
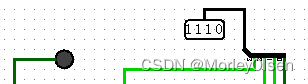
| 1000 | 0110 | 1110 | 0 |
| |||
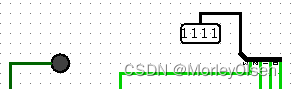
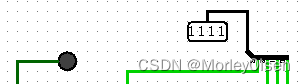
| 1000 | 0111 | 1111 | 0 |
|
| 1000 | 1000 | 0000 | 1 |
| |||
| 1000 | 1001 | 0001 | 1 |
| |||
| 1000 | 1010 | 0010 | 1 |
| |||
| 1000 | 1011 | 0011 | 1 |
| |||
| 1000 | 1100 | 0100 | 1 |
| |||
| 1000 | 1101 | 0101 | 1 |
| |||
| 1000 | 1110 | 0110 | 1 |
| |||
| 1000 | 1111 | 0111 | 1 |
|
减法情况【由于Y和X同时变化时,X-Y状态较多,因此此处仅以X为1000不变,Y从0000依次变换到1111为例,列出实验的各项指标的结果】:
| 输入测试Y | 输入测试X | 实验运算结果 | 实验结果最终借位 | 实验结果截图 | |||
| 0000 | 1000 | 1000 | 1 |
| |||
| 0001 | 1000 | 0111 | 1 |
| |||
| 0010 | 1000 | 0110 | 1 |
| |||
| 0011 | 1000 | 0101 | 1 |
| |||
| 0100 | 1000 | 0100 | 1 |
| |||
| 0101 | 1000 | 0011 | 1 |
| |||
| 0110 | 1000 | 0010 | 1 |
| |||
| 0111 | 1000 | 0001 | 1 |
| |||
| 1000 | 1000 | 0000 | 1 |
| |||
| 1001 | 1000 | 1111 | 0 |
| |||
| 1010 | 1000 | 1110 | 0 |
| |||
| 1011 | 1000 | 1101 | 0 |
| |||
| 1100 | 1000 | 1100 | 0 |
| |||
| 1101 | 1000 | 1011 | 0 |
| |||
| 1110 | 1000 | 1010 | 0 |
| |||
| 1111 | 1000 | 1001 | 0 |
|
时钟自动设定X和Y的数值,并用LED显示计算结果:
该电路图的实验情况类似上述情况,此处不再赘述。
五、实验课后内容
实验3:完成一个32位加减法器
具体要求:
(1)计数器C1,C2输入X、Y。
(2)利用Logisim 库中的加法器实现。
实验步骤:
(1)实验设计分析
本实验的设计思路与实验2的设计思路基本一致。可以通过时钟来控制C1和C2,通过数据选择器控制当前运算执行加法还是减法。如果选择加法,则将C1以原码输入系统的集成加法器;如果选择减法,则将C1取补码后输入系统的集成加法器,最后通过显示器显示运算结果。
(2)实验连线图
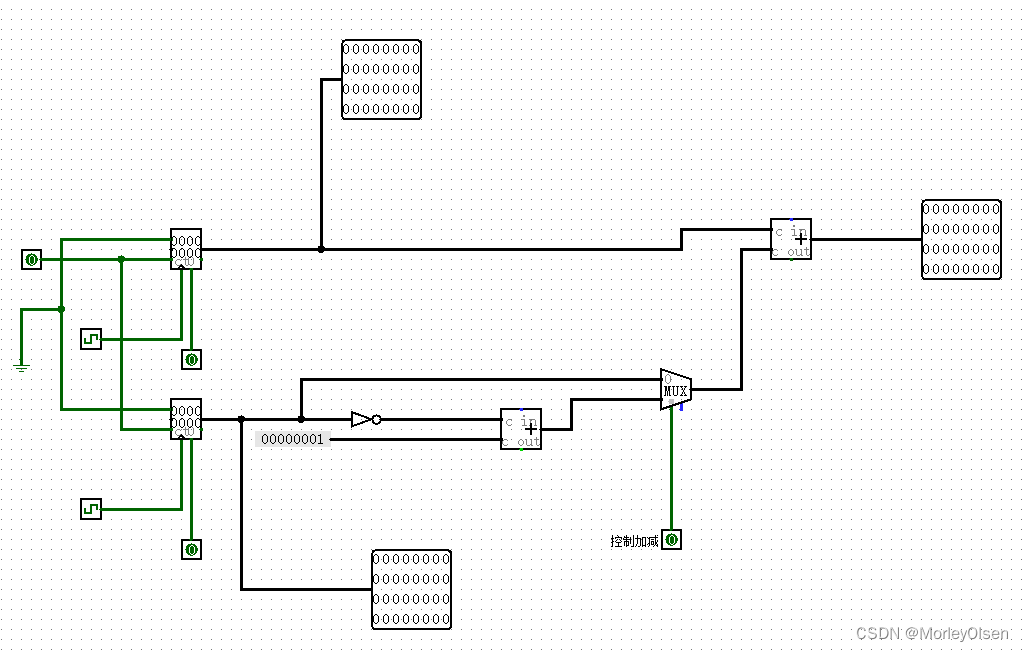
(3)实验结果图
相关案例如附件中video.mkv所示。
六、实验中遇到的问题和解决办法
无。