1.题目

问题1
该数学建模的第一问和第二问主要是用Matlab求解微分方程组,直接编程即可。
求解
Step1改写
- y(1)=r
- y(2)=f
Step2得y的导数
- y(1).=2y(1)-ay(1)*y(2)
- y(2).=-y(2)+a*y(1)*y(2)
Step3编程
clear;
a=0.01;
F=@(t,y)[2*y(1)-a*y(1)*y(2);
-y(2)+a*y(1)*y(2)];
[t,y]=ode45(F,[0,10],[300,150]);
subplot(121);
plot(t,y(:,1));
xlabel('时间');
ylabel('r数量');
subplot(122);
plot(y(:,1),y(:,2));
xlabel('r数量');
ylabel('y数量');
Step4结果
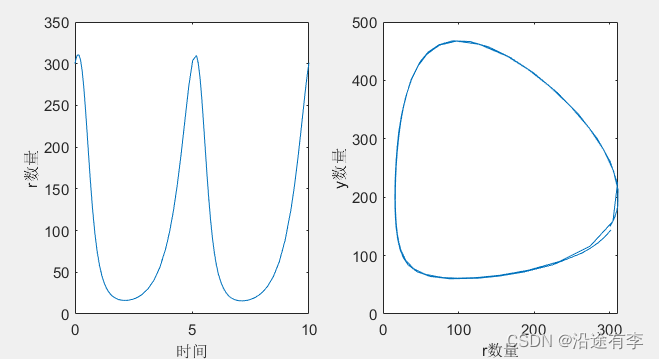
从图中可以看出对应的周期tp大概是5
问题2
改变初值就行啦,直接进入step3
求解
Step3编程
clear;
a=0.01;
F=@(t,y)[2*y(1)-a*y(1)*y(2);
-y(2)+a*y(1)*y(2)];
[t,y]=ode45(F,[0,10],[15,22]);
subplot(121);
plot(t,y(:,1));
xlabel('时间');
ylabel('r数量');
subplot(122);
plot(y(:,1),y(:,2));
xlabel('r数量');
ylabel('y数量');
Step4结果
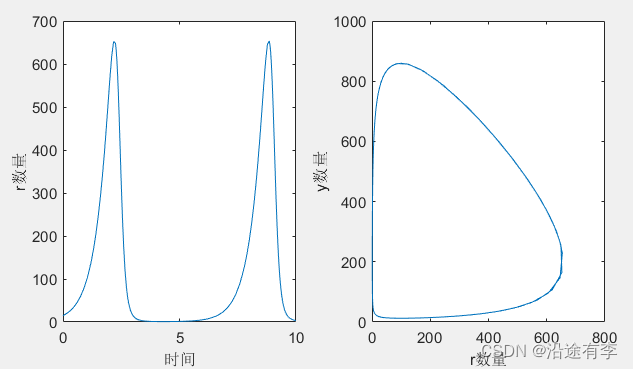
从图中可以看出对应的周期tp大概是8
问题3
分析
首先列公式,给了u和v的定义,咱就对它求导,然后把它代入捕食者方程,再把r和f用u和v替换,根据题目所说忽略二阶项uv,这样可以算得
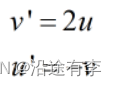
求解
Step1改写
- y(1)=u
- y(2)=v
Step2得y的导数
- y(1).=-y(2)
- y(2).=2y(1)
Step3编程
clear;
a=0.01;
F=@(t,y)[-y(2);
2*y(1)];
[t,y]=ode45(F,[0,10],[0.1,0.1]);
subplot(121);
plot(t,y(:,1));
xlabel('时间');
ylabel('u');
subplot(122);
plot(y(:,1),y(:,2));
xlabel('u');
ylabel('v');
Step4结果
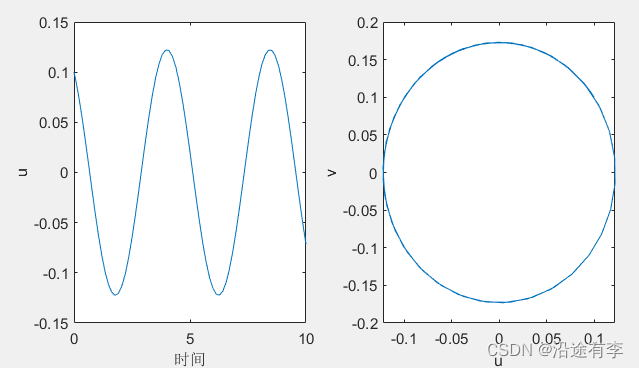
从图中可以看出u对应的周期tp大概是5