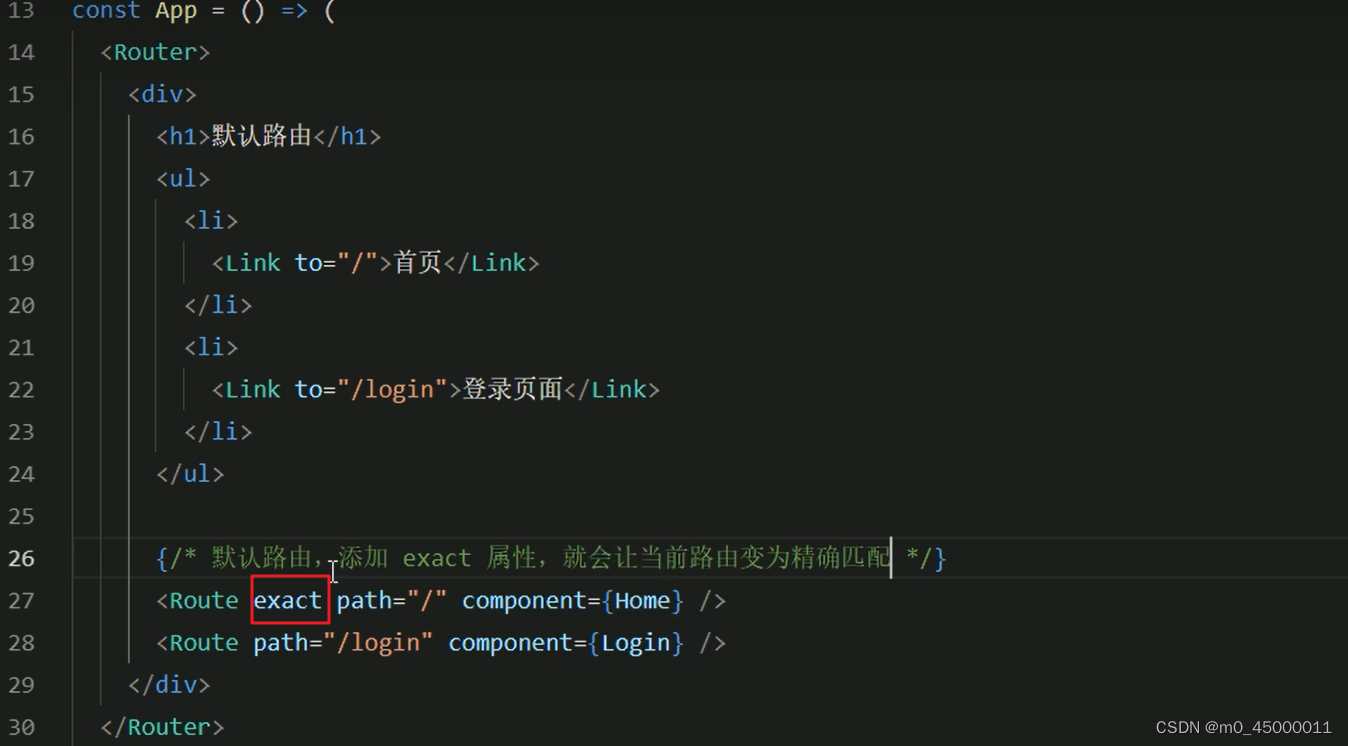
题目链接

环形链表 II

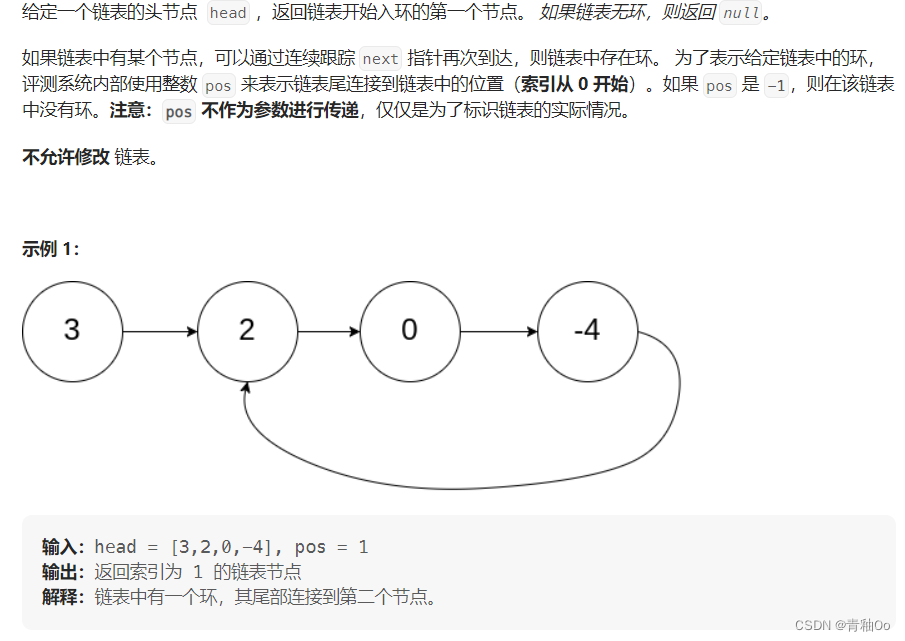
题目描述

注意点

• 如果 pos 是 -1，则在该链表中没有环

解答思路

• 首先判断链表中是否有环，思路为双指针
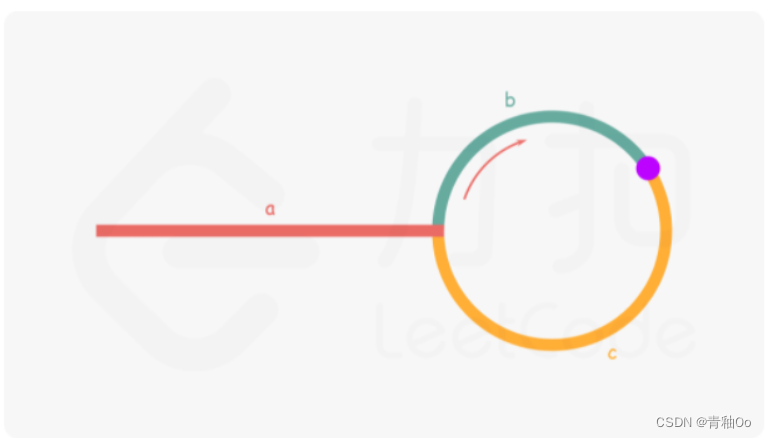
• 当快慢指针相遇时，说明链表中有环，假设链表中非环的节点数量为a，链表中环的节点数量为b，则此时快指针跑过的距离为f = a + b + c（其中c为在环中跑了c距离后快慢指针相遇），慢指针跑过的距离为s = a + c，且此时f = 2s，可以推出b = a + c，而此时快慢指针都在c处，所以只要慢指针继续往前跑a的距离就到达了环开始的位置，也就是再设置一个指针从头节点开始也往前跑a的距离，此时两个指针相遇处就是环的第一个节点，如图所示

代码

/**
 * Definition for singly-linked list.
 * class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode(int x) {
 *         val = x;
 *         next = null;
 *     }
 * }
 */
public class Solution {
    public ListNode detectCycle(ListNode head) {
        ListNode slow = head, quick = head;
        while (quick != null && quick.next != null) {
            quick = quick.next.next;
            slow = slow.next;
            if (quick == slow) {
                quick = head;
                while (quick != slow) {
                    quick = quick.next;
                    slow = slow.next;
                }
                return quick;
            }
        }
        return null;
    }
}

关键点

• 理解双指针相遇时各自前进的距离
• 数学公式推出非环节点数量与环节点数量与快慢指针前进距离之间的关系