文章目录
- Q1:6451. 找出最大的可达成数字(脑筋急转弯?)
- 思路
- 竞赛时代码
- Q2:6899. 达到末尾下标所需的最大跳跃次数(DP)
- 思路
- 竞赛时代码
- Q3:6912. 构造最长非递减子数组(DP)
- 思路
- 竞赛时代码
- Q4:6919. 使数组中的所有元素都等于零
- 思路——贪心+记录每个数字对之后的影响
- 竞赛时代码
- 成绩记录
https://leetcode.cn/contest/weekly-contest-353
Q1:6451. 找出最大的可达成数字(脑筋急转弯?)
https://leetcode.cn/problems/find-the-maximum-achievable-number/
思路
每次可以将差异减少2,一共可以操作 t 次,所以可达成的数字范围是:
[
x
−
2
∗
t
,
x
+
2
∗
t
]
[x - 2 * t, x + 2 * t]
[x−2∗t,x+2∗t]
其中的最大值是
x
+
2
∗
t
x + 2 * t
x+2∗t
竞赛时代码
class Solution {
public int theMaximumAchievableX(int num, int t) {
return num + 2 * t;
}
}

Q2:6899. 达到末尾下标所需的最大跳跃次数(DP)
https://leetcode.cn/problems/maximum-number-of-jumps-to-reach-the-last-index/
最开始想错方向了!以为是 BFS 求最短路!
结果是求最长路。。。
思路
数据范围是
1000
1000
1000
可以选择
O
(
n
2
)
O(n^2)
O(n2) 的时间复杂度的算法。
枚举每个位置,在枚举每个位置时检查可以从前面哪些位置转移过来,并更新达到当前位置所需的最大跳跃次数。
dp数组初始化 为 -1,表示到不了这个位置,dp[0] = 0,表示不用跳就能到。
状态转移方程为: d p [ i ] = M a t h . m a x ( d p [ i ] , d p [ j ] + 1 ) ; dp[i] = Math.max(dp[i], dp[j] + 1); dp[i]=Math.max(dp[i],dp[j]+1);,表示能从 j 跳过来那跳跃次数就 + 1。
竞赛时代码
class Solution {
public int maximumJumps(int[] nums, int target) {
int n = nums.length;
int[] dp = new int[n]; // dp[i]表示达到i的最大跳跃次数
Arrays.fill(dp, -1); // -1表示到不了这个位置
dp[0] = 0;
for (int i = 1; i < n; ++i) {
for (int j = 0; j < i; ++j) {
// 能从j跳过来且j可以被达到
if (Math.abs(nums[i] - nums[j]) <= target && dp[j] != -1) {
dp[i] = Math.max(dp[i], dp[j] + 1);
}
}
}
return dp[n - 1];
}
}
时间复杂度:
O
(
n
2
)
O(n^2)
O(n2)
空间复杂度:
O
(
n
)
O(n)
O(n)
Q3:6912. 构造最长非递减子数组(DP)
https://leetcode.cn/problems/longest-non-decreasing-subarray-from-two-arrays/
思路
看数据范围,大概率使用 O ( n ) O(n) O(n) 的算法。
考虑 DP。
dp[i][0] 表示 第 i 个位置选 nums1[i] 和 nums2[i] 中较小值时,以nums3[i]为结尾的最大子数组长度
dp[i][1] 表示 第 i 个位置选 nums1[i] 和 nums2[i] 中较大值时,以nums3[i]为结尾的最大子数组长度
枚举每个下标 i,则要么选择
n
u
m
s
1
[
i
]
nums1[i]
nums1[i],要么选择
n
u
m
s
2
[
i
]
nums2[i]
nums2[i],选择时的最大长度可以从上个状态
i
−
1
i - 1
i−1 转移过来。
通过比较数值大小判断能否转移,如果能够转移过来,那长度为
M
a
t
h
.
m
a
x
(
d
p
[
i
]
,
d
p
[
j
]
+
1
)
Math.max(dp[i], dp[j] + 1)
Math.max(dp[i],dp[j]+1)。
竞赛时代码
class Solution {
public int maxNonDecreasingLength(int[] nums1, int[] nums2) {
int n = nums1.length, ans = 1, last = Math.min(nums1[0], nums2[0]);
int[][] dp = new int[n][2];
dp[0][1] = dp[0][0] = 1; // 分别记录当前选较小值或最大值时的最大长度
int lastmn = Math.min(nums1[0], nums2[0]), lastmx = Math.max(nums1[0], nums2[0]);
for (int i = 1; i < n; ++i) {
dp[i][0] = dp[i][1] = 1;
int mn = Math.min(nums1[i], nums2[i]), mx = Math.max(nums1[i], nums2[i]);
// 检查是否可以状态转移过来
if (mn >= lastmn) dp[i][0] = Math.max(dp[i][0], dp[i - 1][0] + 1);
if (mn >= lastmx) dp[i][0] = Math.max(dp[i][0], dp[i - 1][1] + 1);
if (mx >= lastmn) dp[i][1] = Math.max(dp[i][1], dp[i - 1][0] + 1);
if (mx >= lastmx) dp[i][1] = Math.max(dp[i][1], dp[i - 1][1] + 1);
lastmn = mn;
lastmx = mx;
ans = Math.max(ans, Math.max(dp[i][0], dp[i][1]));
}
return ans;
}
}
可以看到 dp[i] 的状态只会从 dp[i - 1] 转移过来,即无后效性,可以优化 dp 数组成变量节省空间。
时间复杂度:
O
(
n
)
O(n)
O(n)
空间复杂度:
O
(
n
)
O(n)
O(n)
Q4:6919. 使数组中的所有元素都等于零
https://leetcode.cn/problems/apply-operations-to-make-all-array-elements-equal-to-zero/
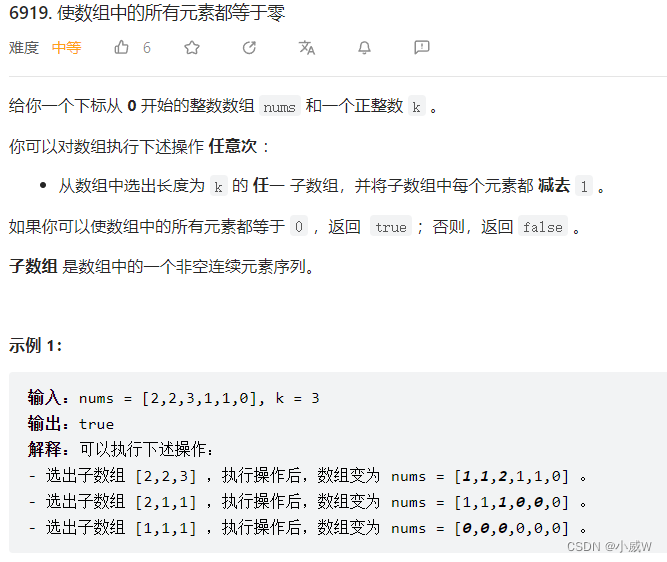
提示:
1 <= k <= nums.length <= 10^5
0 <= nums[i] <= 10^6
思路——贪心+记录每个数字对之后的影响
我们从前往后枚举,当前数字 < 0 时返回 false, == 0 时不需要操作, > 0 时一定是减到 0的。(贪心)
每个位置 i 减去一个数字时,后面紧接着的 k - 1 个数字(也就是以 i 为开头的大小为 k 的窗口内的其它所有数字)。
我们用一个变量 sum 记录前面 k - 1 个数字对 i 的影响。
或者解释说:
对于位置靠前的数,如果前面的数的操作都不足以让其减为0(小于0直接返回False),则直接在当前位置操作(如果不在此处操作,后面的操作无法影响前面),用前缀和记录一下修改的数值即可。
竞赛时代码
class Solution {
public boolean checkArray(int[] nums, int k) {
int n = nums.length, sum = 0; // sum是当前位置被前面k-1个位置影响减去的数值
int[] d = new int[n];
for (int i = 0; i < n; ++i) {
// sum减去被移除窗口位置对应元素贡献的减去值,因为i-k影响不到i
if (i >= k) sum -= d[i - k];
// nums[i]会被前面的数值影响减成负数,不合理
if (nums[i] < sum) return false;
// 如果是最后k-1个数字,直接判断是否为0
// 因为长度不够k了,所以最后的k-1个元素不能操作了。(不能作为窗口开始位置)
if (nums[i] - sum != 0 && i > n - k) return false;
else {
// 计算num[i]还需要减多少到0
d[i] = nums[i] - sum;
sum += d[i];
}
}
return true;
}
}

成绩记录

4道 easy 题,但是我是傻逼!写的也太慢了!老是想歪。
写题的顺序是 1 2 4 3
第一题 39 s,多么美妙的开局!
但是!
怎么第 2 题是DP呀?
第 2 题是 DP 就算了怎么第 3 题还是 DP 呀?你会不会出点别的题!?
凎!
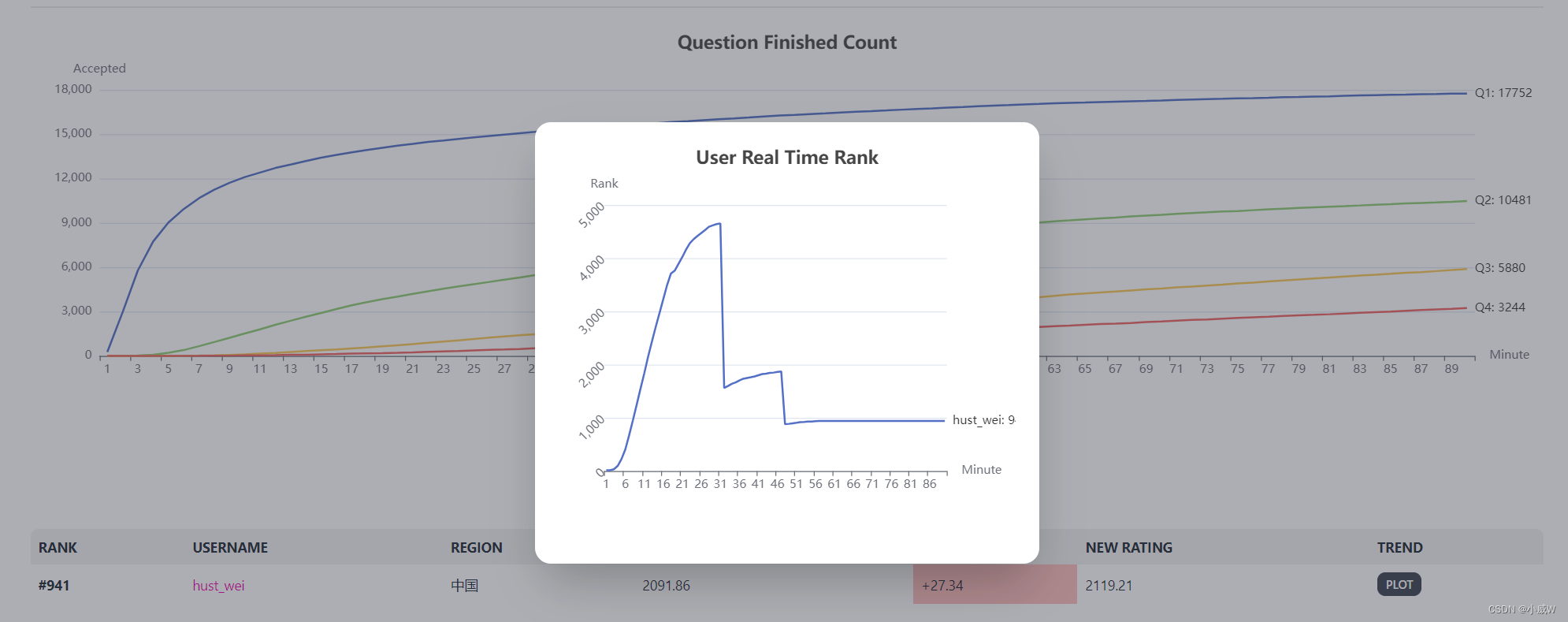
结束之后看了下别人写的题解,基本上和我也差不多,所以就还好。







![火车头小发猫AI伪原创[php源码]](https://img-blog.csdnimg.cn/6b0790b51d7f4bf192da2d3e2ff6f57a.png)