一、绪论
数据结构是计算机科学中的一门基础课程,研究数据的存储、组织和管理方法,以及在这些数据上进行各种操作的算法和技术。掌握数据结构和算法是编程中非常重要的基础,对于实现高效、可靠的程序至关重要。常见的数据结构包括数组、链表、栈、队列、树和图等。理解不同数据结构的特点和适用场景,并选择合适的数据结构,再应用相应的算法来解决问题,是我们在实际编程中所需要掌握的技能。
1、 数据结构的基本概念
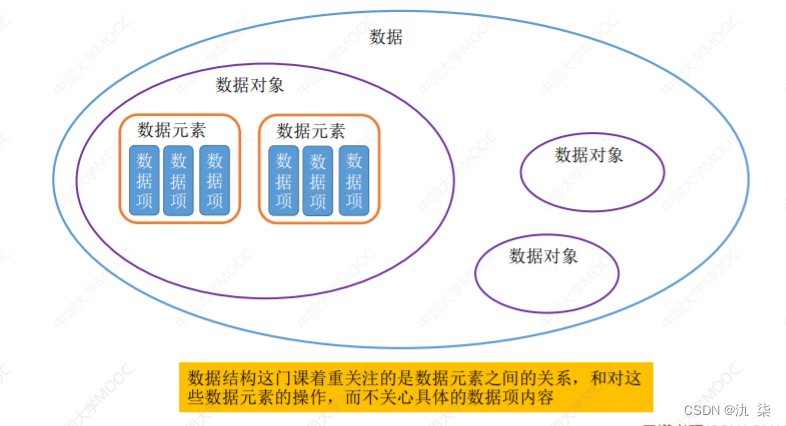
数据元素是指构成数据的基本单位,它可以是数字、字符、字符串、结构体等,数据元素之间可以存在不同的关系,如有序关系、无序关系、父子关系等。
数据项是指数据元素中的数据成员,例如:学生记录就是一个数据元素,它由学号、姓名、性别等数据项祖成。
数据对象是具有相同性质数据元素的集合,是数据的一个子集。如整数数据对象。
数据类型是值的集合和定义在此集合上的一组操作的总称。
抽象数据类型是指一种数据类型的抽象描述,它包含了数据元素的逻辑结构、数据元素之间的关系以及对这些数据元素进行操作的一组操作集合。抽象数据类型不考虑具体的实现方式,而是关注数据类型的抽象描述,它的实现可以采用不同的数据结构。可以定义一个完整的数据结构。
2、数据结构三要素
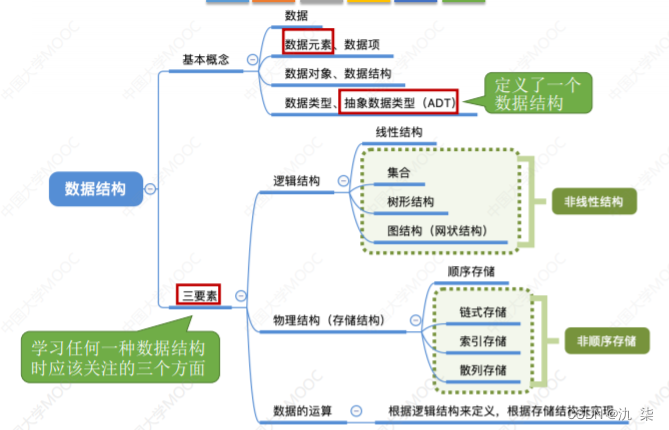
数据结构是指数据元素之间的关系,包括数据的逻辑结构、数据的存储结构和数据的运算。其中,数据的逻辑结构是指数据元素之间的逻辑关系,包括线性结构(栈、队列、数组、串)、非线性结构(树形结构、图状结构、集合)。数据的存储结构是指数据在计算机内部的存储方式,包括数据的表示和关系的表示。数据的运算是指对数据进行操作和处理的方法,包括查找、排序、插入、删除等操作。
逻辑结构是独立于存储结构的,可以通过不同的存储结构来实现。
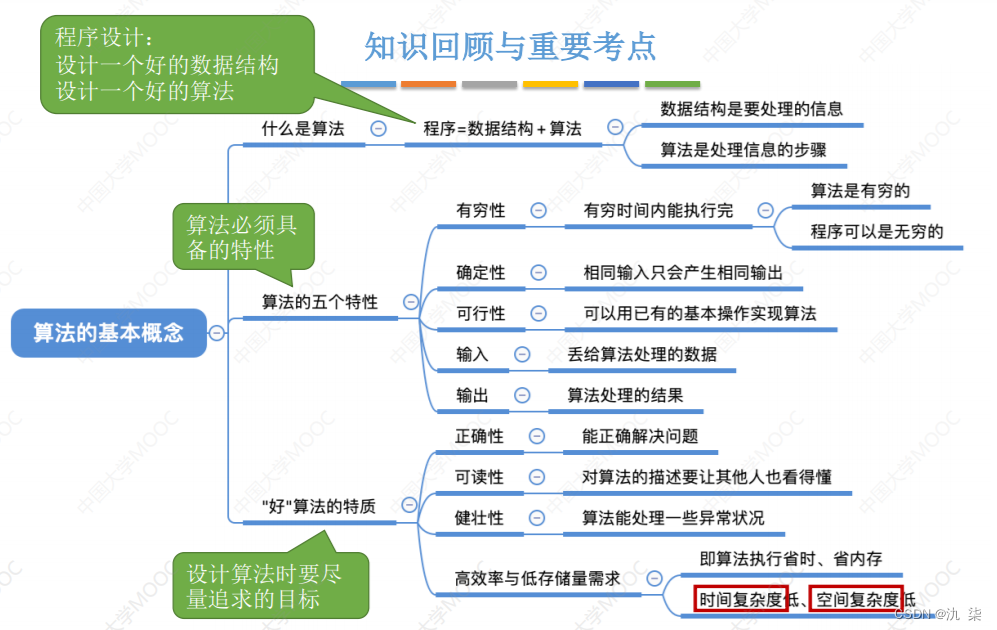
3、算法和算法评价

算法是指解决问题的一系列步骤。具有5个特性:
输入:0或至少1个输入(可以理解为入参)。
输出:至少一个。
有穷性:算法通过有限步骤解决问题,不会死循环。
确定性:算法解决每个步骤有特定的作用;通常算法只有一条执行路径,相同输入出现一个结果;无歧义。
可行性:每一步骤通过有限步骤执行。
好的算法应考虑以下4个目标:
正确性:正确求解问题
可读性:便于人们理解
健壮性:对非法数据有良好的处理
高效率与低存储量:算法在执行时间和所需存储空间方面的效率应尽可能高,能够处理大规模数据和复杂任务。
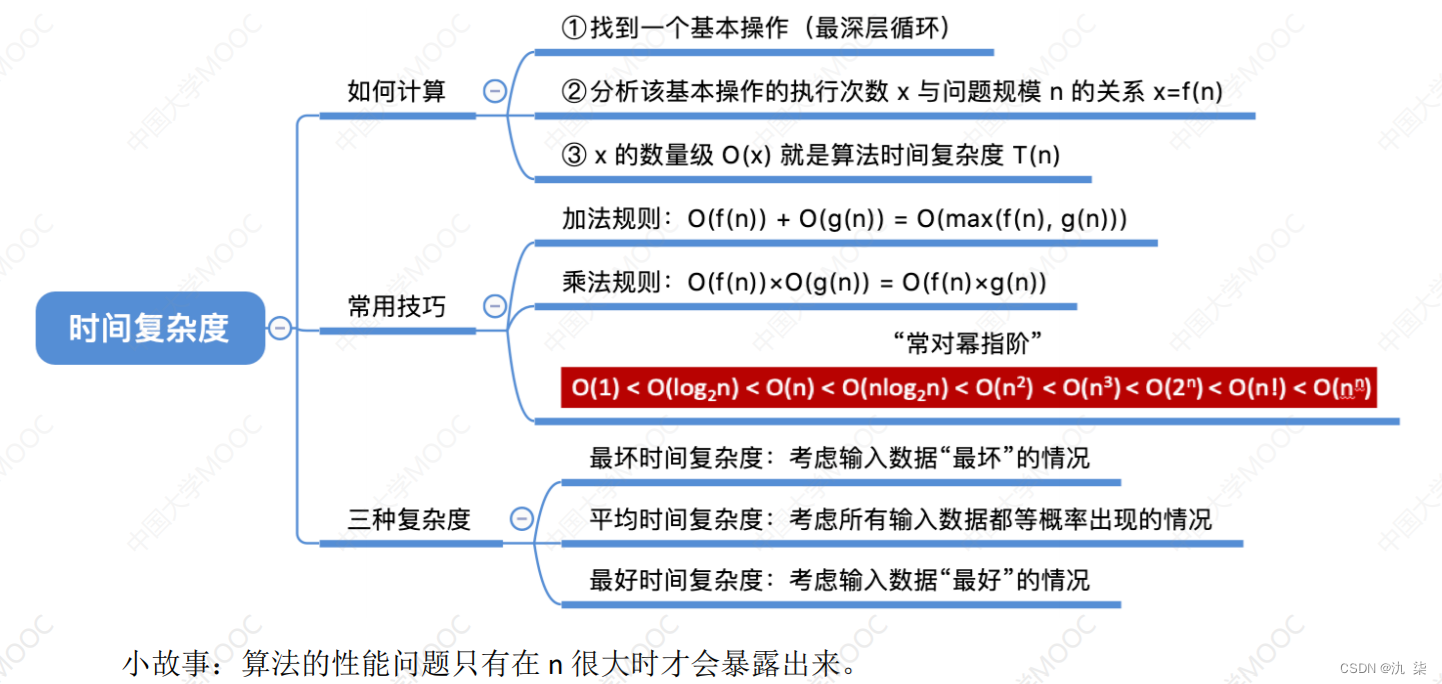
时间复杂度是算法执行时间随输入规模的增长而增长的量度,通常用大O记法表示。计算时间复杂度的方法如下:
关注最高阶项:在计算时间复杂度时,主要关注算法中最高阶项的执行次数。因为最高阶项通常对算法的执行时间具有决定性的影响。其他低阶项和常数项对于大规模输入来说相对较小,可以忽略。
忽略常数项:在时间复杂度的计算中,通常可以忽略算法中的常数项。因为常数项对于大规模输入的影响较小,而主要关注算法的增长趋势。
使用大O记法:大O记法是一种表示时间复杂度的常用方法。它表示算法执行时间的增长趋势,而不是精确的执行时间。大O记法将时间复杂度表示为一个函数,用来描述算法执行时间与输入规模之间的关系。常见的时间复杂度包括O(1)、O(log n)、O(n)、O(n log n)、O(n^2)等。
考虑最坏情况:在计算时间复杂度时,通常考虑算法在最坏情况下的执行时间。因为最坏情况下的时间复杂度提供了对算法性能的保守估计,确保算法在任何情况下都不会超过这个时间限制。
分析循环和递归:对于循环结构和递归算法,需要分析每次循环或递归调用的执行次数,并将其与输入规模相关联。这样可以得到算法的总体执行次数,从而计算时间复杂度。
使用算法分析工具和技巧:有许多常用的算法分析工具和技巧可用于计算时间复杂度,例如递推关系、求和公式、主定理等。这些工具和技巧可以帮助简化计算过程并得到更精确的时间复杂度结果。
最坏时间复杂度:最坏情况下算法的时间复杂度
平均时间复杂度:所有输入示例等概率出现的情况下,算法的期望运行时间
最好时间复杂度:最好情况下算法的时间复杂度
需要注意的是,时间复杂度的计算是对算法在最坏情况下的执行时间进行分析。最坏情况下的时间复杂度提供了一种保守的估计,确保算法在任何情况下都能满足时间限制。




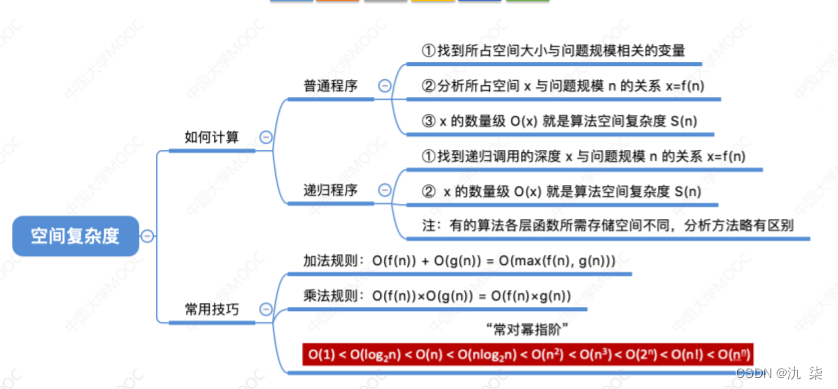
空间复杂度是衡量算法执行所需的额外空间随输入规模增长的量度。它表示算法在运行过程中所需要的额外存储空间,通常包括算法本身使用的空间和辅助数据结构所需的空间。
空间复杂度的表示通常也使用大O记法,用来衡量额外空间的增长趋势。与时间复杂度类似.计算算法的空间复杂度涉及到评估算法在执行过程中所需的额外空间资源。以下是一些常用的方法和指导原则来求解算法的空间复杂度:
确定变量和数据结构的空间消耗:分析算法中使用的变量和数据结构,并确定它们在内存中的空间消耗。例如,对于数组,需要考虑数组的长度乘以每个元素所占用的空间;对于链表,需要考虑每个节点的空间消耗以及额外的指针等。
考虑递归调用的空间:如果算法包含递归调用,需要考虑递归调用过程中所使用的栈空间。递归算法的空间复杂度通常与递归深度有关。
考虑额外的辅助空间:除了变量和数据结构之外,有些算法可能需要额外的辅助空间来存储临时结果或执行某些操作。例如,归并排序中使用的临时数组,或者深度优先搜索中使用的栈。
分析空间的使用情况:对于迭代算法,可以逐步分析算法执行过程中的空间使用情况。可以跟踪每个操作的空间消耗,并计算总体的空间复杂度。
根据空间的增长趋势估算复杂度:根据算法中所使用的空间资源的增长趋势,使用大O记法来表示空间复杂度。例如,如果算法的额外空间消耗与输入规模呈线性关系,则可以表示为O(n);如果空间消耗与输入规模的平方呈正比,则可以表示为O(n^2)。
需要注意的是,空间复杂度的计算通常是对算法在最坏情况下的空间使用进行分析。最坏情况下的空间复杂度提供了一种保守的估计,确保算法在任何情况下都不会超过这个空间限制。
总而言之,计算空间复杂度需要分析算法中所使用的变量、数据结构和额外空间,并根据其使用情况和增长趋势来估算空间复杂度。这样可以帮助我们评估算法的空间资源消耗,选择合适的算法,并进行性能优化。
当一个算法在执行过程中只使用常数级别的额外空间,并且不需要依赖于输入规模的增长,我们称其为原地工作(In-place)算法。
原地工作算法的优点在于它们能够节省额外的空间资源,并且在处理大规模数据时更具效率。原地工作算法通常通过在输入数据上进行原地修改和重排,而不是创建额外的数据结构来存储中间结果。
一些常见的原地工作算法包括:
- 原地排序算法:例如快速排序和堆排序。这些算法通过在原始数据中交换元素的位置来实现排序,而不需要额外的数组来存储中间结果。
- 链表操作算法:在链表中进行插入、删除和翻转等操作时,可以只使用常数级别的额外指针来修改节点的链接,而不需要额外的空间。
- 数组操作算法:例如数组反转、去重、移除元素等操作,可以在原始数组上进行原地修改,而不需要额外的数组来存储中间结果。
- 搜索算法:某些搜索算法,如深度优先搜索(DFS)和广度优先搜索(BFS),可以通过修改节点的状态来避免额外的空间开销。
在设计原地工作算法时,需要仔细考虑如何利用输入数据本身的特性,合理安排修改操作的顺序,以确保算法的正确性和效率。