167. 两数之和 II - 输入有序数组
给你一个下标从 1 开始的整数数组 numbers ,该数组已按 非递减顺序排列 ,请你从数组中找出满足相加之和等于目标数 target
的两个数。如果设这两个数分别是 numbers[index1] 和 numbers[index2] ,则 1 <= index1 <
index2 <= numbers.length 。以长度为 2 的整数数组 [index1, index2] 的形式返回这两个整数的下标 index1 和 index2。
你可以假设每个输入 只对应唯一的答案 ,而且你 不可以 重复使用相同的元素。
你所设计的解决方案必须只使用常量级的额外空间。
示例 1:
输入:numbers = [2,7,11,15], target = 9
输出:[1,2]
解释:2 与 7 之和等于目标数 9 。因此 index1 = 1, index2 = 2 。返回 [1, 2] 。
示例 2:
输入:numbers = [2,3,4], target = 6
输出:[1,3]
解释:2 与 4 之和等于目标数 6 。因此 index1 = 1, index2 = 3 。返回 [1, 3] 。
示例 3:
输入:numbers = [-1,0], target = -1
输出:[1,2]
解释:-1 与 0 之和等于目标数 -1 。因此 index1 = 1, index2 = 2 。返回 [1, 2] 。
两种方法:O(n)双指针法和O(nlogn)的二分查找法
//方法二:双指针法 O(n)
class Solution {
public int[] twoSum(int[] numbers, int target) {
int[] res = new int[2];
int left=0,right=numbers.length-1;
while(left<right){
if(numbers[left]+numbers[right]<target) left++;
else if(numbers[left]+numbers[right]>target) right--;
else {
res[0]=left+1;
res[1]=right+1;
break;
}
}
return res;
}
//方法一:O(nlogn) 二分查找
public int[] twoSum(int[] numbers, int target) {
int[] res = new int[2];
int key=0;
//思路是:双指针/二分查找/数组
for(int i=0;i<numbers.length-1;i++){
key=target-numbers[i];
//二分查找
int index=binarySearch(numbers,key,i+1,numbers.length-1);
if(index==-1) continue;
else{
res[0]=i+1;
res[1]=index+1;
break;
}
}
return res;
}
int binarySearch(int[] numbers, int key, int left, int right) {
if(left>right) return -1;
int mid=(right+left)/2;
if(numbers[mid]>key) return binarySearch(numbers, key, left, mid-1);
else if(numbers[mid]==key) return mid;
else return binarySearch(numbers, key, mid+1, right);
}
}
Khan拓扑排序算法
207. 课程表
你这个学期必须选修 numCourses 门课程,记为 0 到 numCourses - 1 。
在选修某些课程之前需要一些先修课程。 先修课程按数组 prerequisites 给出,其中 prerequisites[i] = [ai,
bi] ,表示如果要学习课程 ai 则 必须 先学习课程 bi 。例如,先修课程对 [0, 1] 表示:想要学习课程 0 ,你需要先完成课程 1 。 请你判断是否可能完成所有课程的学习?如果可以,返回
true ;否则,返回 false 。
示例 1:
输入:numCourses = 2, prerequisites = [[1,0]]
输出:true
解释:总共有 2 门课程。学习课程 1 之前,你需要完成课程 0 。这是可能的。
示例 2:
输入:numCourses = 2, prerequisites = [[1,0],[0,1]]
输出:false
解释:总共有 2 门课程。学习课程 1 之前,你需要先完成课程 0 ;并且学习课程 0 之前,你还应先完成课程 1 。这是不可能的。
提示:
1 <= numCourses <= 105
0 <= prerequisites.length <= 5000
prerequisites[i].length == 2
0 <= ai, bi < numCourses
prerequisites[i] 中的所有课程对 互不相同
class Solution {
public boolean canFinish(int numCourses, int[][] prerequisites) {
/*
统计每个课被指向次数,初始被指向次数为0的肯定是安全的(不在环上)。
每被安全课程指向一次,被指次数减一,
如果被指次数减到0,说明该课程全部指向都来自安全课程,则它也是安全的。
依此进行队列循环。
拓扑排序不用区分什么广度优先深度优先把自己弄乱了,抓住节点入度和出度的本质特征。 方法一: 从入度思考(从前往后排序), 入度为0的节点在拓扑排序中一定排在前面, 然后删除和该节点对应的边, 迭代寻找入度为0的节点。 方法二: 从出度思考(从后往前排序), 出度为0的节点在拓扑排序中一定排在后面, 然后删除和该节点对应的边, 迭代寻找出度为0的节点。
*/
int[] point=new int[numCourses]; //记录每个课程被指向的次数
int len=prerequisites.length;
for(int[] p:prerequisites){
point[p[0]]++;
}
boolean[] removed=new boolean[len];
int remove=0;
while(remove<len){
int currentRemove=0;
for(int i=0;i<len;i++){
if(removed[i]) continue; //该规则已被删除
int[] p=prerequisites[i];
if(point[p[1]]==0){ //判断指向课程的是否为安全课程,是的话就可以删除该规则。
point[p[0]]--;
removed[i]=true;
currentRemove++;
}
}
if(currentRemove==0) return false; // 如果一轮跑下来一个元素都没移除,则没必要进行下一轮
remove+=currentRemove;
}
return true;
}
}
210. 课程表 II
现在你总共有 numCourses 门课需要选,记为 0 到 numCourses - 1。给你一个数组 prerequisites ,其中
prerequisites[i] = [ai, bi] ,表示在选修课程 ai 前 必须 先选修 bi 。例如,想要学习课程 0 ,你需要先完成课程 1 ,我们用一个匹配来表示:[0,1] 。
返回你为了学完所有课程所安排的学习顺序。可能会有多个正确的顺序,你只要返回 任意一种 就可以了。如果不可能完成所有课程,返回 一个空数组 。
示例 1:
输入:numCourses = 2, prerequisites = [[1,0]]
输出:[0,1]
解释:总共有 2 门课程。要学习课程 1,你需要先完成课程 0。因此,正确的课程顺序为 [0,1] 。
示例 2:
输入:numCourses = 4, prerequisites = [[1,0],[2,0],[3,1],[3,2]]
输出:[0,2,1,3]
解释:总共有 4 门课程。要学习课程 3,你应该先完成课程 1 和课程 2。并且课程 1 和课程 2 都应该排在课程 0 之后。
因此,一个正确的课程顺序是 [0,1,2,3] 。另一个正确的排序是 [0,2,1,3] 。
示例 3:
输入:numCourses = 1, prerequisites = []
输出:[0]
提示:
1 <= numCourses <= 2000
0 <= prerequisites.length <= numCourses * (numCourses - 1)
prerequisites[i].length == 2
0 <= ai, bi < numCourses
ai != bi
所有[ai, bi] 互不相同
class Solution {
public int[] findOrder(int numCourses, int[][] prerequisites) {
int[] res=new int[numCourses]; //记录返回的课程学习顺序
int index=0;
int[] point=new int[numCourses]; //记录每个课程的入度,入度为0的时候是安全课程可以进行学习
for(int[] p:prerequisites){
point[p[0]]++;
}
for(int i=0;i<numCourses;i++){
if(point[i]==0){
res[index++]=i;
}
}
int len=prerequisites.length;
boolean[] removed=new boolean[len];
int remove=0;
while(remove<len){
int currentRemove=0;
for(int i=0;i<len;i++){
if(removed[i]) continue;
int[]p =prerequisites[i];
if(point[p[1]]==0){
point[p[0]]--;
removed[i]=true;
currentRemove++;
if(point[p[0]]==0) res[index++]=p[0];
}
}
if(currentRemove==0){
return new int[0];
}
remove+=currentRemove;
}
return res;
}
}
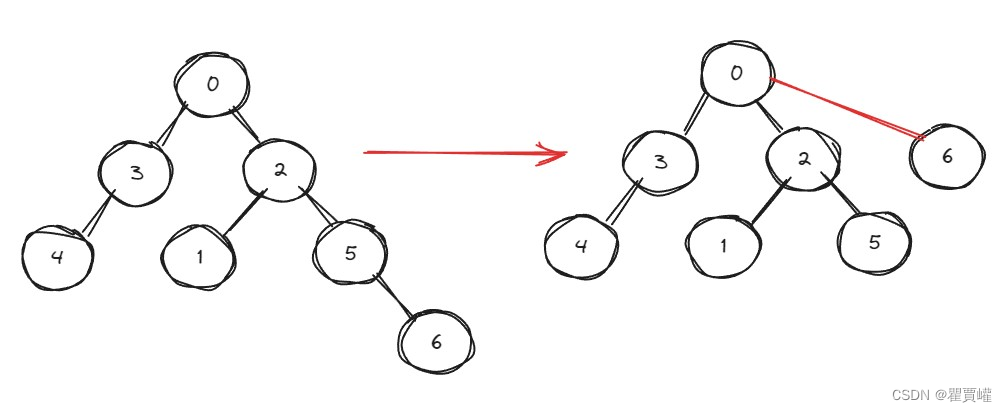
拓扑排序算法重点看入度,入度为0可以放入队列中,然后依次取出队列中元素,切断该元素与后续元素的连接,即相关元素的入度全部-1,同时判断入度是否为0,为0则进入队列。循环进行取队列中元素...
236. 二叉树的最近公共祖先
给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。
百度百科中最近公共祖先的定义为:“对于有根树 T 的两个节点 p、q,最近公共祖先表示为一个节点 x,满足 x 是 p、q 的祖先且 x
的深度尽可能大(一个节点也可以是它自己的祖先)。”
示例 1:
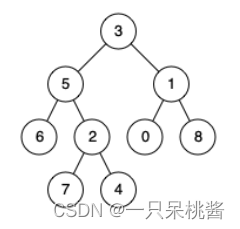
输入:root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 1
输出:3
解释:节点 5 和节点 1 的最近公共祖先是节点 3 。
示例 2:
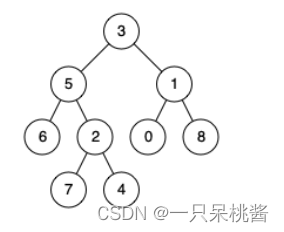
输入:root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 4
输出:5
解释:节点 5 和节点 4 的最近公共祖先是节点 5 。因为根据定义最近公共祖先节点可以为节点本身。
提示:
树中节点数目在范围 [2, 105] 内。
-109 <= Node.val <= 109
所有 Node.val 互不相同 。
p != q
p 和 q 均存在于给定的二叉树中。
根据以上定义,若 root 是 p,q 的 最近公共祖先 ,则只可能为以下情况之一:
p 和 q 在 root 的子树中,且分列 root 的 异侧(即分别在左、右子树中);
p=root ,且 q 在 root 的左或右子树中;
q=root ,且 p 在 root的左或右子树中;
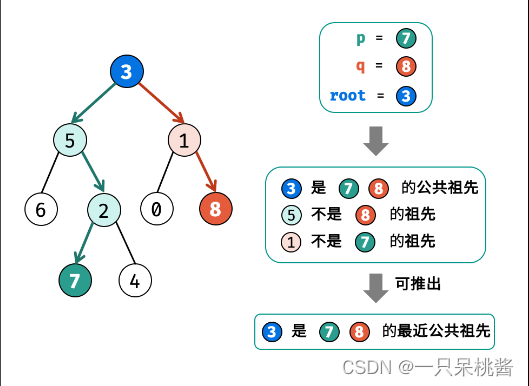
考虑通过递归对二叉树进行先序遍历,当遇到节点 p 或 q 时返回。从底至顶回溯,当节点 p,q, 在节点root的异侧时,节点 root即为最近公共祖先,则向上返回 root 。
递归解析: 终止条件: 当越过叶节点,则直接返回 null; 当 root等于 p,q,则直接返回 root; 递推工作: 开启递归左子节点,返回值记为 left;开启递归右子节点,返回值记为 right; 返回值: 根据 left和 right,可展开为四种情况; 当 left和 right同时为空 :说明root的左 / 右子树中都不包含 p,q ,返回 null; 当 left和right同时不为空 :说明 p,q 分列在 root 的 异侧 (分别在 左 / 右子树),因此 root为最近公共祖先,返回 root; 当 left为空,right不为空 :p,q 都不在 root的左子树中,直接返回right 。具体可分为两种情况: p,q 其中一个在 root 的 右子树 中,此时right 指向 p(假设为 p ); p,q 两节点都在root 的 右子树中,此时的right 指向 最近公共祖先节点 ; 当 left 不为空,right 为空 :与情况 3. 同理;
class Solution {
public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
//二叉树的深度优先搜索dfs,可以用栈完成
if(root==null||root==p||root==q) return root;
TreeNode left=lowestCommonAncestor(root.left,p,q);
TreeNode right=lowestCommonAncestor(root.right,p,q);
if(left!=null&&right!=null) return root;
if(left!=null) return left;
return right;
}
}