并查集的概述

并查集是一种用于解决集合合并和查询问题的数据结构，主要用于实现有关集合的操作，它有两种主要操作，合并（union）和查找（find）。

1. 查找（Find）：用来确定元素属于哪个集合。它接受一个元素作为参数，并返回这个元素所属集合的代表元素。通过查找操作，可以判断两个元素是否属于同一个集合。
2. 合并（Union）：用于将两个集合合并成一个集合。它接受两个元素作为参数，并将这两个元素所属的集合进行合并。合并操作可以将两个不相交的集合合并成一个集合。

并查集由一组集合构成，其中每个集合标识了一个由元素组成的不相交的子集。每个集合有一个代表元素，通常是集合中的某个元素，代表元素可以用来唯一标识一个集合。

并查集的主要用途

1. 可以判断两个元素是否属于同一集合：可以解决连接性问题，比如判断网络中两个节点之间是否存在连通路径
2. 判断图中是否有环存在：逐条遍历图中的边，不断执行合并操作，如果尝试合并两个已经在同一个集合中的元素，则说明存在环路
3. 求连通分量
4. 图的最小生成树算法
5. 动态等价关系：判断社交网络中两个人是否是朋友关系

并查集的实现

创建和初始化集合

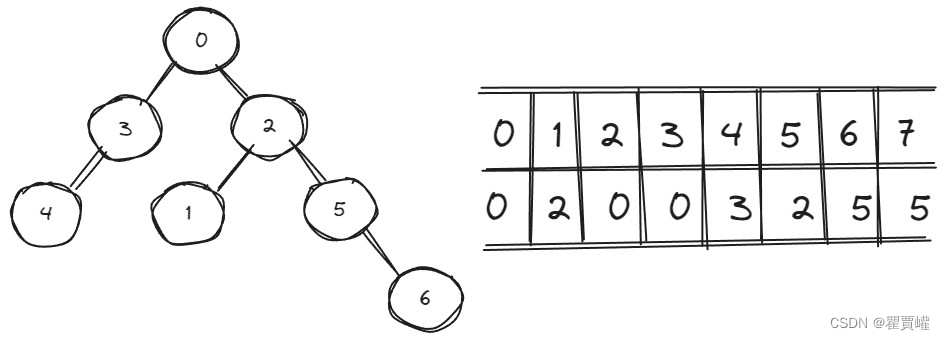
    private int[] ids;// 集合

    public UnionFind1(int[] arr) {
        int length = arr.length;
        ids = new int[length];
        for (int i = 0; i < length; i++) {
            ids[i] = i;
        }
    }

查找当前元素的集合根节点

    public int findParent(int index) {
        // 递归终止条件
        if (index == this.parent[index]) {
            return this.parent[index];
        }
        return findParent(parent[index]);
    }

判断两个元素是否处于同一集合

    public boolean isConnected(int p, int q) {
        return findParent(p) == findParent(q);
    }

合并两个集合

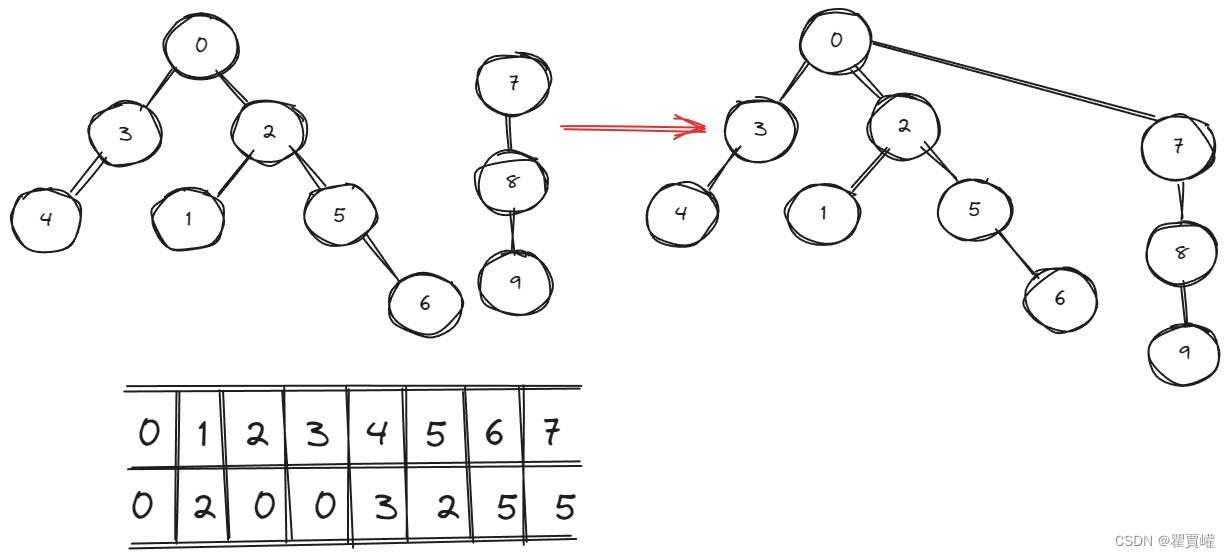
将节点少的树合并到节点多的树

    public void union(int p, int q) {
        int pFather = findParent(p);
        int qFather = findParent(q);
        if (pFather != qFather) {
            if (sz[pFather] > sz[qFather]) {
                this.parent[qFather] = pFather;
                sz[pFather] = sz[qFather];
            } else {
                this.parent[pFather] = qFather;
                sz[qFather] = sz[pFather];
            }
        }
    }

将高度小的树合并到高度大的树

    public void union(int p, int q) {
        int pFather = findParent(p);
        int qFather = findParent(q);
        if (pFather != qFather) {
            if (rank[pFather] > rank[qFather]) {
                this.parent[qFather] = pFather;
            } else if (rank[pFather] < rank[qFather]) {
                this.parent[pFather] = qFather;
            } else{
                this.parent[pFather] = qFather;
                rank[qFather] += 1;
            }
        }
    }

对节点的路径进行压缩

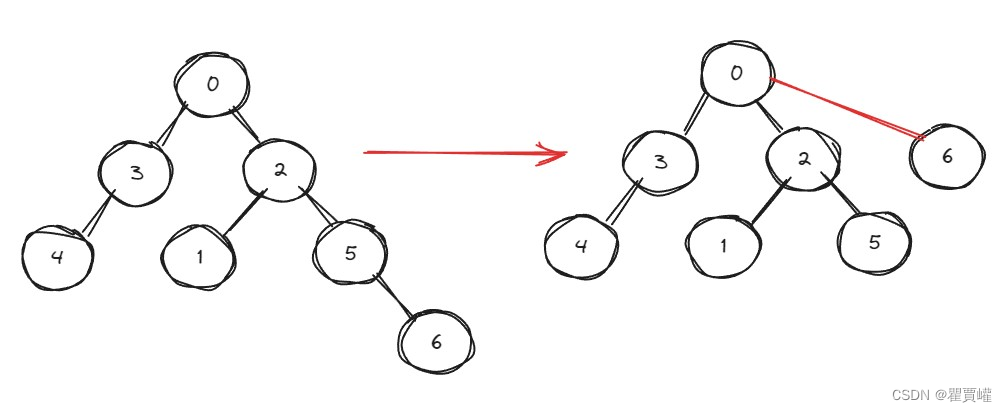
    // 压缩方式一
    public int findParent(int index) {
        // 递归终止条件
        if (index == this.parent[index]) {
            return this.parent[index];
        }
        parent[index] = parent[parent[index]];
        return findParent(parent[index]);
    }

	// 压缩方式二
	public int findParent(int index) {
        // 递归终止条件
        int curIndex = index;
        while (curIndex != parent[curIndex]) {
            curIndex = parent[curIndex];
        }
        parent[index] = curIndex;
        return curIndex;
    }