本博客内容为参考B站视频做的笔记
大家多学习，努力考💯💯💯！！！

离散数学公式
!符号 代码 含义
$\wedge$ \wedge 且
$\vee$ \vee 或
$\cap$ \cap 交
$\cup$ \cup 并
$\subseteq$ \subseteq 子集
$⊈$ \nsubseteq 不是子集
$\subset$ \subset 真子集
$\not\subset$ \not\subset 不是真子集
$\in$ \in 属于
$\notin$ \not\in 不属于
$\leftrightarrow$ \leftrightarrow 等价
$\iff$ \Leftrightarrow 等值
$\neg$ \neg或\lnot 非
$\mathbb{R}$ \mathbb{R} 实数集
$\mathbb{Z}$ \mathbb{Z} 整数集
$\varnothing$ \varnothing 空集
$\forall$ \forall 对任意的
$\exists$ \exists 存在

1. 离散数学与组合数学大纲要求

离散数学与组合数学是现代数学的重要分支，是计算机科学的基础理论课程。数理逻辑、集合论、图论与代数结构是离散数学的重要组成部分。要求考生对它们的基本概念有较深入的了解，能够系统地掌握命题演算、谓词演算及朴素集合论的经典内容，掌握演绎推理的基本方法。 掌握图论的基本定理和应用，熟悉代数系统的基本概念及定理。
组合数学部分要求考生掌握各种基本的计数方法，线性常系数递推关系的解法，Burnside引理和Polya定理的应用，容斥原理和鸽巢原理的应用等。

概述

1.1 离散数学概述

偏重计算机科学

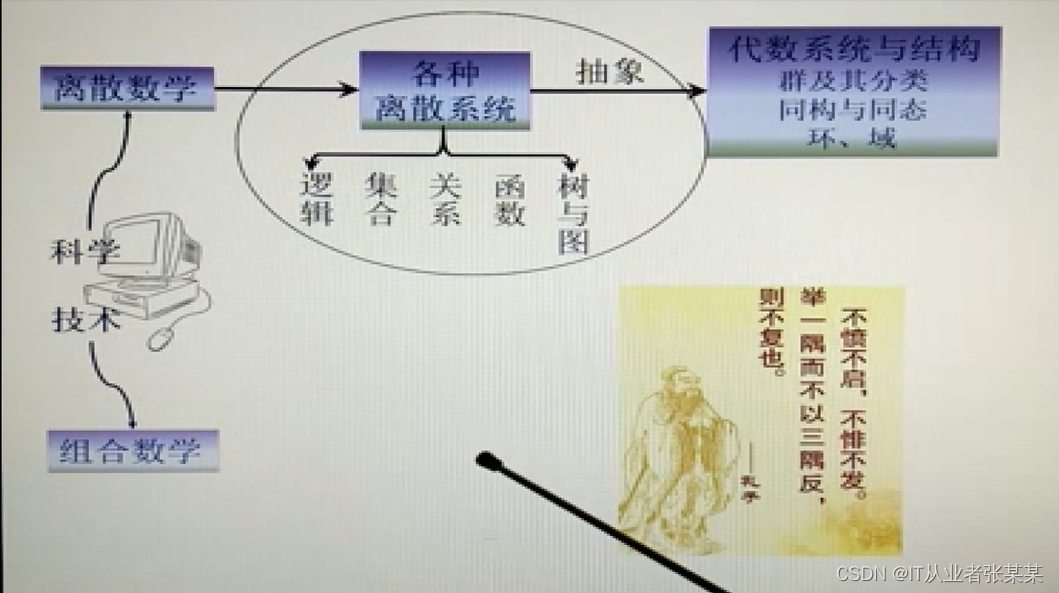
1.2 组合数学概述

偏重计算机技术

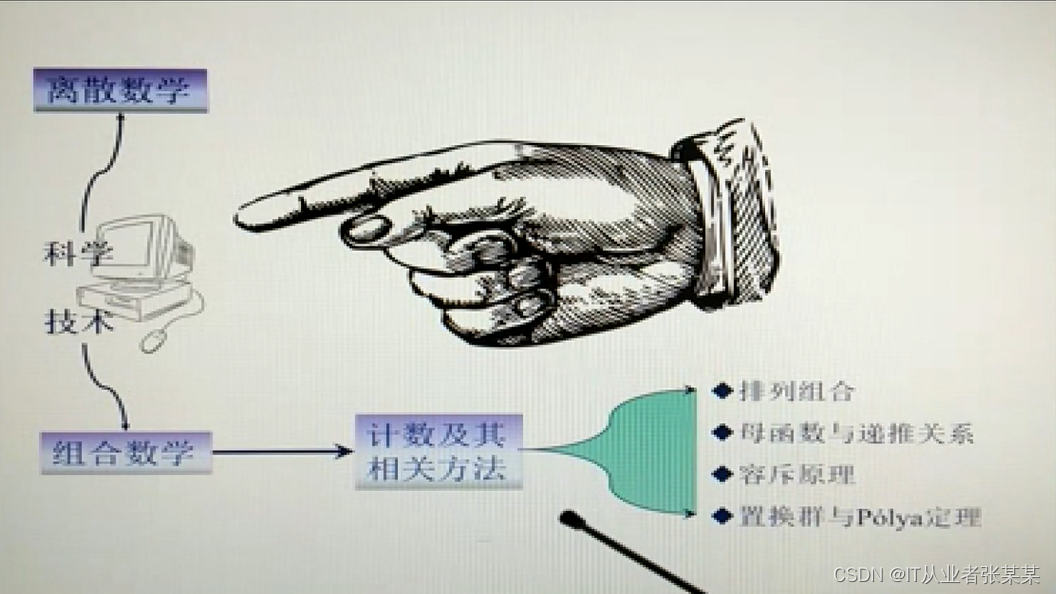
1.3. 离散数学前言

离散数学是研究离散数据关系和离散结构数学模型的数学分支的统称，是计算机科学与技术专业的核心基础课程。

计算机求解问题的基本模式：
实际问题–>数学建模–>算法设计–>编程实现
其中数学建模是把连续模型过度到连续模型。

第1章 数理逻辑

数理逻辑(mathematical logic)是用数学的方法来研究人类推理过程的一门数学学科。其显著特征是符号化和形式化,即把逻辑所涉及的“概念、判断、推理”用符号来表示,用公理体系来刻划,并基于符号串形式的演算来描述推理过程的一般规律。又称符合逻辑和现代逻辑

逻辑验算的四个分支：

公理集合论 重点讲
证明论 讲部分案例
模型论
递归论

1.1 命题与联结词

1. 命题

命题：我们对确定对象做出的陈述句称为命题（propositions and statements 命题或陈述）。当判断为真时，该命题为真，否则为假。

原子命题:通常把不含有逻辑联结词的命题称为原子命题或原子(atoms)
复合命题:把由原子命题和逻辑联结词共同组成的命题称为复合命题(compositive propositions or compound statements 综合命题或复合命题)。

2.联结词

2.集合论

3.代数系统

4.图论