sklearn中的特征选择feature_selection

news2024/11/16 19:54:42

特征选择

概念：就是从所有的特征中，选择出有意义，对模型有帮助的特征，以避免必须将所有特征都导入模型去训练的情况。
特征选择常用的方法有：过滤法，嵌入法，包装法，和降维算法

过滤法

sklearn.feature_selection.VarianceThreshold 方差阈值法

sklearn.feature_selection.VarianceThreshold 方差阈值法，用于特征选择，过滤器法的一种，去掉那些方差没有达到阈值的特征。默认情况下，删除零方差的特征。

若数据维度较高，并且需要剔除一些特征，那么依据每个特征所携带的信息熵进行过滤是一种简便快速的特征筛选方法。

from sklearn.feature_selection import VarianceThreshold
from sklearn.datasets import load_iris
iris = load_iris()
print(iris.data[0:5])
#方差选择法，返回值为特征选择后的数据 #参数threshold为方差的阈值
selector = VarianceThreshold(threshold=1).fit(iris.data, iris.target)
data = selector.transform(iris.data)
print(data[0:5])
print(selector.variances_)

from sklearn.feature_selection import VarianceThreshold
import numpy as np
X = [[0, 2, 0, 3], [0, 1, 4, 3], [0, 1, 1, 3]]
X=np.array(X)
print('原始数据',X.shape)
selector = VarianceThreshold()
data=selector.fit_transform(X)
print('过滤后的数据',data.shape)
print('方差',selector.variances_)

 根据方差的中位数进行过滤

import numpy as np
from sklearn.datasets import make_blobs
from sklearn.feature_selection import VarianceThreshold
data,label=make_blobs(n_features=800,n_samples=100,centers=4,random_state=1218)

print('数据的维度',data.shape)
print('标签的维度',label.shape)
# print('数据的方差',data.var(axis=0))
print('数据方差的中位数',np.median(data.var(axis=0)))
selector = VarianceThreshold(np.median(data.var(axis=0))) #实例化，不填参数默认方差为0
new_data=selector.fit_transform(data)
print('新数据的维度',new_data.shape)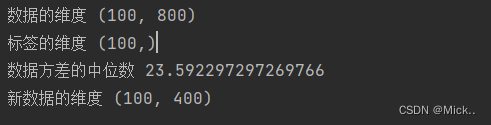

 

方差过滤对模型的影响

  1. 最近邻算法KNN，单棵决策树，支持向量机SVM，神经网络，回归算法，都需要遍历特征或升维来进行运算，所以他们本身的运算量就很大，需要的时间就很长，因此方差过滤这样的特征选择对他们来说就尤为重要。
  2. 但对于不需要遍历特征的算法，比如随机森林，它随机选取特征进行分枝，本身运算就非常快速，因此特征选择对它来说效果平平。

过滤法的主要对象是：需要遍历特征或升维的算法们;
过滤法的主要目的是：在维持算法表现的前提下，帮助算法们降低计算成本。

如果过滤之后模型的效果反而变差了，那么被过滤掉的特征中有很多是有效特征，就需要放弃过滤

相关性过滤

方差挑选完毕之后，我们就要考虑下一个问题：相关性了。我们希望选出与标签相关且有意义的特征，因为这样的特征能够为我们提供大量信息。如果特征与标签无关，那只会白白浪费我们的计算，可能还会给模型带来噪音。在sklearn当中，我们有三种常用的方法来评判特征与标签之间的相关性：卡方，F检验，互信息。

卡方过滤

卡方过滤是专门针对离散型标签（即分类问题）的相关性过滤。卡方检验类feature_selection.chi2计算每个非负特征和标签之间的卡方统计量，并依照卡方统计量由高到低为特征排名。再结合feature_selection.SelectKBest这个可以输入”评分标准“来选出前K个分数最高的特征的类，我们可以借此除去最可能独立于标签，与我们分类目的无关的特征

from sklearn.datasets import make_blobs
from sklearn.ensemble import RandomForestClassifier as RFC
from sklearn.model_selection import cross_val_score
from sklearn.feature_selection import SelectKBest
from sklearn.feature_selection import chi2
from sklearn.preprocessing import MinMaxScaler
import numpy as np
data,label=make_blobs(n_features=800,n_samples=100,centers=4,random_state=1218)
#将数据缩放到0-1之间
scaler=MinMaxScaler(feature_range=(0,1))
data=scaler.fit_transform(data)
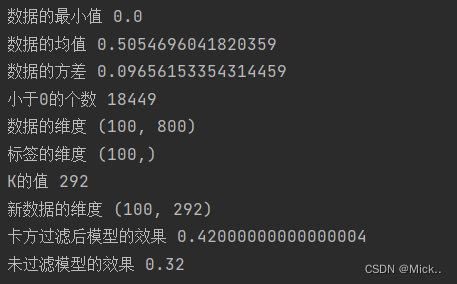
print('数据的最小值',data.min())
print('数据的均值',data.mean())
print('数据的方差',data.var())

##加入高斯噪声 生成随机正太分布
noise=np.random.normal(loc=1,scale=2,size=(100,800))
data=data+noise
#这里因为卡方检验feature_selection.chi2 计算的是非负特征与标签的卡方统计量
print('小于0的个数',np.sum(data<0))
data[data<0]=0
print('数据的维度',data.shape)
print('标签的维度',label.shape)

#卡方过滤
new_data=SelectKBest(chi2,k=200).fit_transform(data,label)
print('新数据的维度',new_data.shape)

#验证一下卡方过滤后的效果
print('卡方过滤后模型的效果',cross_val_score(RFC(n_estimators=10,random_state=0),new_data,label,cv=5).mean())
print('未过滤模型的效果',cross_val_score(RFC(n_estimators=10,random_state=0),data,label,cv=5).mean())

选取超参数K

卡方检验的本质是推测两组数据之间的差异，其检验的原假设是”两组数据是相互独立的”。卡方检验返回卡方值和P值两个统计量，我们可以根据P值进行筛选，p<=0.05或0.01,说明两组数据是相关的。
从特征工程的角度，我们希望选取卡方值很大，p值小于0.05的特征，即和标签是相关联的特征。

from sklearn.datasets import make_blobs
from sklearn.ensemble import RandomForestClassifier as RFC
from sklearn.model_selection import cross_val_score
from sklearn.feature_selection import SelectKBest
from sklearn.feature_selection import chi2
from sklearn.preprocessing import MinMaxScaler
import numpy as np
import matplotlib.pyplot as plt
data,label=make_blobs(n_features=800,n_samples=100,centers=4,random_state=1218)
#将数据缩放到0-1之间
scaler=MinMaxScaler(feature_range=(0,1))
data=scaler.fit_transform(data)
print('数据的最小值',data.min())
print('数据的均值',data.mean())
print('数据的方差',data.var())

##加入高斯噪声 生成随机正太分布
noise=np.random.normal(loc=1,scale=2,size=(100,800))
data=data+noise
#这里因为卡方检验feature_selection.chi2 计算的是非负特征与标签的卡方统计量
print('小于0的个数',np.sum(data<0))
data[data<0]=0
print('数据的维度',data.shape)
print('标签的维度',label.shape)

##返回卡方值，p值，p<=0.05或0.01,说明两组数据是相关的
chivalue,pvalues_chi=chi2(data,label)
print('卡方值',chivalue)
print('p值',pvalues_chi)
#k取多少？我们想要消除所有p值大于设定值，比如0.05或0.01的特征：
#chivalue.shape[0]就是取出特征总个数，pvalues_chi > 0.05返回TRUE Flase,False=0,TRUE=1,所以就是总特征数减去所以p>0.05的特征，就是想保留的特征的数量
k = chivalue.shape[0] - (pvalues_chi > 0.05).sum()
print('K的值',k)
#卡方过滤
new_data=SelectKBest(chi2,k=k).fit_transform(data,label)
print('新数据的维度',new_data.shape)

#验证一下卡方过滤后的效果
print('卡方过滤后模型的效果',cross_val_score(RFC(n_estimators=10,random_state=0),new_data,label,cv=5).mean())
print('未过滤模型的效果',cross_val_score(RFC(n_estimators=10,random_state=0),data,label,cv=5).mean())

或者是遍历一下 

from sklearn.datasets import make_blobs
from sklearn.ensemble import RandomForestClassifier as RFC
from sklearn.model_selection import cross_val_score
from sklearn.feature_selection import SelectKBest
from sklearn.feature_selection import chi2
from sklearn.preprocessing import MinMaxScaler
import numpy as np
import matplotlib.pyplot as plt
data,label=make_blobs(n_features=800,n_samples=100,centers=4,random_state=1218)
#将数据缩放到0-1之间
scaler=MinMaxScaler(feature_range=(0,1))
data=scaler.fit_transform(data)
print('数据的最小值',data.min())
print('数据的均值',data.mean())
print('数据的方差',data.var())

##加入高斯噪声 生成随机正太分布
noise=np.random.normal(loc=1,scale=2,size=(100,800))
data=data+noise
#这里因为卡方检验feature_selection.chi2 计算的是非负特征与标签的卡方统计量
print('小于0的个数',np.sum(data<0))
data[data<0]=0
print('数据的维度',data.shape)
print('标签的维度',label.shape)

#卡方过滤
new_data=SelectKBest(chi2,k=200).fit_transform(data,label)
print('新数据的维度',new_data.shape)

#验证一下卡方过滤后的效果
print('卡方过滤后模型的效果',cross_val_score(RFC(n_estimators=10,random_state=0),new_data,label,cv=5).mean())
print('未过滤模型的效果',cross_val_score(RFC(n_estimators=10,random_state=0),data,label,cv=5).mean())

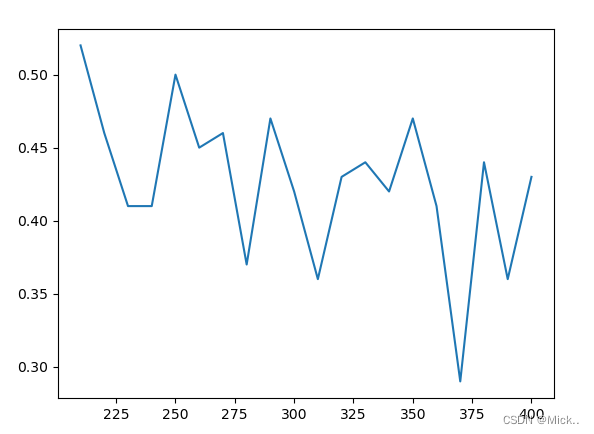
#超参数k的选择
score=[]
for i in range(400,200,-10):
    new_data = SelectKBest(chi2, k=i).fit_transform(data, label)
    score.append(cross_val_score(RFC(n_estimators=10,random_state=0),new_data,label,cv=5).mean())
plt.plot(range(400,200,-10),score)
plt.show()

F检验 

F检验，又称ANOVA，方差齐性检验，是用来捕捉每个特征与标签之间的线性关系的过滤方法。它即可以做回归也可以做分类，因此包含feature_selection.f_classif（F检验分类）和feature_selection.f_regression（F检验回归）两个类。它返回F值和p值两个统计量。和卡方过滤一样，选取p值小于0.05或0.01的特征，这些特征与标签时显著线性相关的。

from sklearn.datasets import make_blobs
from sklearn.ensemble import RandomForestClassifier as RFC
from sklearn.model_selection import cross_val_score
from sklearn.feature_selection import SelectKBest
from sklearn.feature_selection import chi2
from sklearn.preprocessing import MinMaxScaler
import numpy as np
from sklearn.feature_selection import f_classif

data,label=make_blobs(n_features=800,n_samples=100,centers=4,random_state=1218)
#将数据缩放到0-1之间
scaler=MinMaxScaler(feature_range=(0,1))
data=scaler.fit_transform(data)
print('数据的最小值',data.min())
print('数据的均值',data.mean())
print('数据的方差',data.var())

##加入高斯噪声 生成随机正太分布
noise=np.random.normal(loc=1,scale=2,size=(100,800))
data=data+noise
print('数据的维度',data.shape)
print('标签的维度',label.shape)

#F检验
F, pvalues_f = f_classif(data,label)
k = F.shape[0] - (pvalues_f > 0.05).sum()

new_data = SelectKBest(f_classif, k=k).fit_transform(data, label)

print('新数据的维度',new_data.shape)
#验证一下F检验后的效果
print('F检测后模型的效果',cross_val_score(RFC(n_estimators=10,random_state=0),new_data,label,cv=5).mean())
print('原始模型的效果',cross_val_score(RFC(n_estimators=10,random_state=0),data,label,cv=5).mean())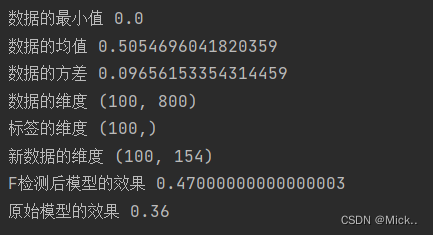

 

互信息法

互信息法是用来捕捉每个特征与标签之间的任意关系（包括线性和非线性关系）的过滤方法。和F检验相似，它既可以做回归也可以做分类，并且包含两个类feature_selection.mutual_info_classif（互信息分类）和feature_selection.mutual_info_regression（互信息回归）。
它返回“每个特征与目标之间的互信息量的估计”，这个估计量在[0,1]之间取值，为0则表示两个变量独立，为1则表示两个变量完全相关。

from sklearn.datasets import make_blobs
from sklearn.ensemble import RandomForestClassifier as RFC
from sklearn.model_selection import cross_val_score
from sklearn.feature_selection import SelectKBest
from sklearn.preprocessing import MinMaxScaler
import numpy as np
from sklearn.feature_selection import mutual_info_classif as  MIC

data,label=make_blobs(n_features=800,n_samples=100,centers=4,random_state=1218)
#将数据缩放到0-1之间
scaler=MinMaxScaler(feature_range=(0,1))
data=scaler.fit_transform(data)
print('数据的最小值',data.min())
print('数据的均值',data.mean())
print('数据的方差',data.var())

##加入高斯噪声 生成随机正太分布
noise=np.random.normal(loc=1,scale=2,size=(100,800))
data=data+noise
print('数据的维度',data.shape)
print('标签的维度',label.shape)

#互信息方法
result=MIC(data,label)
k=result.shape[0]-np.sum(result<=0)
print('k值',k)
new_data = SelectKBest(MIC, k=k).fit_transform(data, label)

print('新数据的维度',new_data.shape)
#验证一下F检验后的效果
print('互信息后模型的效果',cross_val_score(RFC(n_estimators=10,random_state=0),new_data,label,cv=5).mean())
print('原始模型的效果',cross_val_score(RFC(n_estimators=10,random_state=0),data,label,cv=5).mean())

 

Embedded嵌入法

feature_selection.SelectFromModel

嵌入法是一种让算法自己决定使用哪些特征的方法，即特征选择和算法训练同时进行

class sklearn.feature_selection.SelectFromModel (estimator, threshold=None, prefit=False, norm_order=1,max_features=None)

参数：
estimator：使用的模型评估器，只要是带feature_importances_或者coef_属性，或带有l1和l2惩罚项的模型都可以使用。
threshold：特征重要性的阈值，重要性低于这个阈值的特征都将被删除

打印特征的重要性

from sklearn.datasets import make_blobs
from sklearn.ensemble import RandomForestClassifier as RFC
from sklearn.model_selection import cross_val_score
from sklearn.preprocessing import MinMaxScaler
import numpy as np
import matplotlib.pyplot as plt
from sklearn.feature_selection import SelectFromModel

data,label=make_blobs(n_features=800,n_samples=100,centers=4,random_state=1218)
#将数据缩放到0-1之间
scaler=MinMaxScaler(feature_range=(0,1))
data=scaler.fit_transform(data)
print('数据的最小值',data.min())
print('数据的均值',data.mean())
print('数据的方差',data.var())
##加入高斯噪声 生成随机正太分布
noise=np.random.normal(loc=1,scale=2,size=(100,800))
data=data+noise
print('数据的维度',data.shape)
print('标签的维度',label.shape)

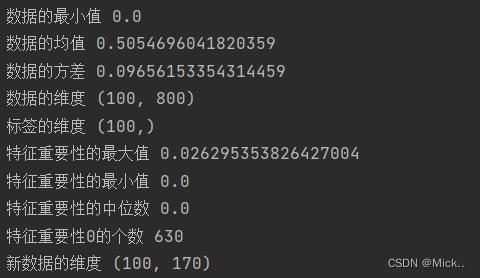
#首先实例化随机森林
RFC_=RFC(n_estimators=10,random_state=1218)

feature_importance=RFC_.fit(data,label).feature_importances_
# print('特征的重要性',feature_importance)
print('特征重要性的最大值',feature_importance.max())
print('特征重要性的最小值',feature_importance.min())
print('特征重要性的中位数',np.median(feature_importance))
print('特征重要性0的个数',np.sum(feature_importance==0))
new_data = SelectFromModel(RFC_,threshold=0.001).fit_transform(data,label) #这个是嵌入法的实例化
print('新数据的维度',new_data.shape)

 ​​​​​​​​​​​​​​​​​​​​​

from sklearn.datasets import make_blobs
from sklearn.ensemble import RandomForestClassifier as RFC
from sklearn.model_selection import cross_val_score
from sklearn.preprocessing import MinMaxScaler
import numpy as np
import matplotlib.pyplot as plt
from sklearn.feature_selection import SelectFromModel

data,label=make_blobs(n_features=800,n_samples=100,centers=4,random_state=1218)
#将数据缩放到0-1之间
scaler=MinMaxScaler(feature_range=(0,1))
data=scaler.fit_transform(data)
print('数据的最小值',data.min())
print('数据的均值',data.mean())
print('数据的方差',data.var())
##加入高斯噪声 生成随机正太分布
noise=np.random.normal(loc=1,scale=2,size=(100,800))
data=data+noise
print('数据的维度',data.shape)
print('标签的维度',label.shape)

#首先实例化随机森林
RFC_=RFC(n_estimators=10,random_state=1218)

new_data = SelectFromModel(RFC_,threshold=0.005).fit_transform(data,label) #这个是嵌入法的实例化

print('新数据的维度',new_data.shape)

# 绘制threshold的学习曲线
threshold = np.linspace(0,(RFC_.fit(data,label).feature_importances_).max(),20) #让阈值的取值在0到最大值之间取出20个数

score = []
for i in threshold:
    X_embedded = SelectFromModel(RFC_,threshold=i).fit_transform(data,label)
    once = cross_val_score(RFC_,X_embedded,label,cv=5).mean()
    score.append(once)

plt.plot(threshold,score)
plt.show()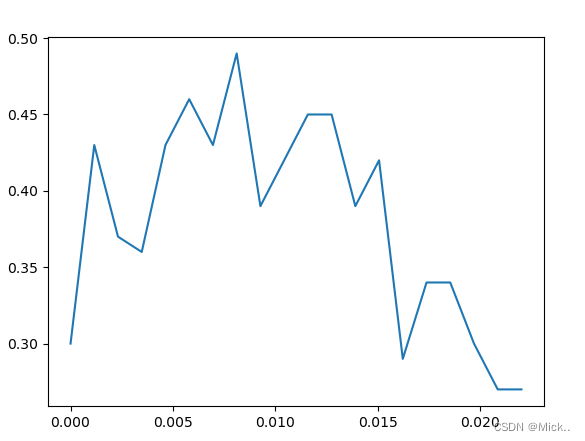

 ​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​

 

 可见，随着阈值越来越高，模型的效果逐渐变差，被删除的特征越来越多，信息损失也逐渐变大

from sklearn.datasets import make_blobs
from sklearn.ensemble import RandomForestClassifier as RFC
from sklearn.model_selection import cross_val_score
from sklearn.preprocessing import MinMaxScaler
import numpy as np
import matplotlib.pyplot as plt
from sklearn.feature_selection import SelectFromModel

data,label=make_blobs(n_features=800,n_samples=100,centers=4,random_state=1218)
#将数据缩放到0-1之间
scaler=MinMaxScaler(feature_range=(0,1))
data=scaler.fit_transform(data)
print('数据的最小值',data.min())
print('数据的均值',data.mean())
print('数据的方差',data.var())
##加入高斯噪声 生成随机正太分布
noise=np.random.normal(loc=1,scale=2,size=(100,800))
data=data+noise
print('数据的维度',data.shape)
print('标签的维度',label.shape)

#首先实例化随机森林
RFC_=RFC(n_estimators=10,random_state=1218)

new_data = SelectFromModel(RFC_,threshold=0.005).fit_transform(data,label) #这个是嵌入法的实例化

print('新数据的维度',new_data.shape)

score = []
for i in np.linspace(0,0.002,20):
    X_embedded = SelectFromModel(RFC_,threshold=i).fit_transform(data,label)
    once = cross_val_score(RFC_,X_embedded,label,cv=5).mean()
    score.append(once)
plt.figure(figsize=[20,5])
plt.plot(np.linspace(0,0.002,20),score)
plt.xticks(np.linspace(0,0.002,20))
plt.show()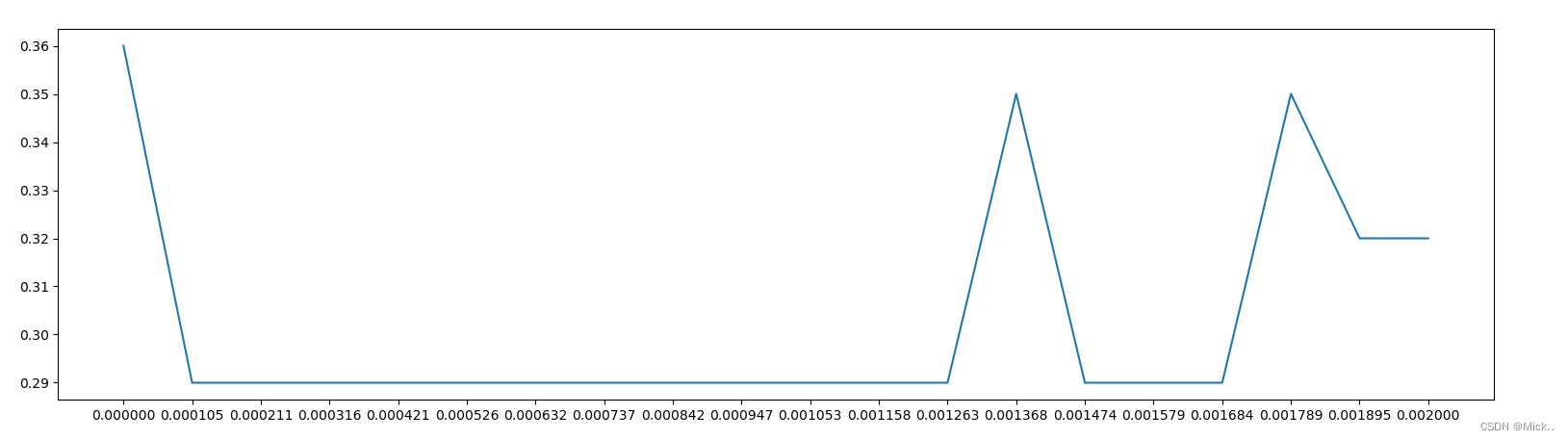

 Wrapper包装法

包装法也是一个特征选择和算法训练同时进行的方法，但我们往往使用一个目标函数作为黑盒来帮助我们选取特征，而不是自己输入某个评估指标或统计量的阈值。。区别于过滤法和嵌入法的一次训练解决所有问题，包装法要使用特征子集进行多次训练，计算成本位于嵌入法和过

class sklearn.feature_selection.RFE (estimator, n_features_to_select=None, step=1, verbose=0)

参数estimator是需要填写的实例化后的评估器，n_features_to_select是想要选择的特征个数，step表示每次迭代中希望移除的特征个数。
除此之外，RFE类有两个很重要的属性，.support_：返回所有的特征的是否最后被选中的布尔矩阵，以及.ranking_返回特征的按数次迭代中综合重要性的排名。

 

from sklearn.datasets import make_blobs
from sklearn.ensemble import RandomForestClassifier as RFC
from sklearn.model_selection import cross_val_score
from sklearn.preprocessing import MinMaxScaler
import numpy as np
from sklearn.feature_selection import RFE

data,label=make_blobs(n_features=800,n_samples=100,centers=4,random_state=1218)
#将数据缩放到0-1之间
scaler=MinMaxScaler(feature_range=(0,1))
data=scaler.fit_transform(data)
print('数据的最小值',data.min())
print('数据的均值',data.mean())
print('数据的方差',data.var())
##加入高斯噪声 生成随机正太分布
noise=np.random.normal(loc=1,scale=2,size=(100,800))
data=data+noise
print('数据的维度',data.shape)
print('标签的维度',label.shape)

RFC_ = RFC(n_estimators =10,random_state=0) #实例化RFC
#n_features_to_select是模型选择的个数，step每迭代一次删除50个特征
selector = RFE(RFC_, n_features_to_select=332, step=50).fit(data, label) #RFE的实例化和训练 332是上述模型效果最好时的特征数

print(selector.support_.sum()) #support_返回特征是否被选中的布尔矩阵，求和其实就是n_features_to_select
print(selector.ranking_) #返回特征的重要性排名
X_wrapper = selector.transform(data)
#交叉验证验证模型
cross_val_score(RFC_,X_wrapper,label,cv=5).mean()

特征选择总结

  1. 当数据量很大的时候，优先使用方差过滤和互信息法调整，再上其他特征选择方法。
  2. 使用逻辑回归时，优先使用嵌入法。
  3. 使用支持向量机时，优先使用包装法。

 

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/73251.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

BN128曲线

BN128曲线

1. 引言 BN系列椭圆曲线E(Fp):y2x3b&#xff0c;其中b≠0E(\mathbb{F}_p):y^2x^3b&#xff0c;其中b\neq 0E(Fp​):y2x3b&#xff0c;其中b​0&#xff0c;由Paulo S. L. M. Barreto1 和 Michael Naehrig 在2005年论文 Pairing-Friendly Elliptic Curves of Prime Order中首…
阅读更多...
增长思维 —— 撬动企业增长的杠杆

增长思维 —— 撬动企业增长的杠杆

增长一定不是只适用于互联网公司 营销&#xff1a;获客 增长&#xff1a;研究的是用户全生命周期 增长思维&#xff1a;以供需分析为基础&#xff0c;从用户全生命周期寻找增长点的方法论 这个模型的核心是啊哈时刻&#xff0c;指的是一个产品对用户价值感最强的那个点 一个…
阅读更多...
画饼画到世界地图上：按比例呈现多组数据

画饼画到世界地图上：按比例呈现多组数据

地图是数据可视化的一部分&#xff0c;做群体遗传学、动物学、植物学、微生物学等的朋友经常用到世界地图&#xff0c;比如绘制不同小麦品种的世界分布。一般情况下&#xff0c;我们根据经纬度将数据标注在地图上&#xff0c;然而有些时候&#xff0c;我们会需要更高级的标注&a…
阅读更多...
Apache doris 1.2.0 release

Apache doris 1.2.0 release

亲爱的社区小伙伴们&#xff0c;再一次经历数月的等候后&#xff0c;我们很高兴地宣布&#xff0c;Apache Doris 于 2022 年 12 月 7 日迎来 1.2.0 Release 版本的正式发布&#xff01;有近 118 位 Contributor 为 Apache Doris 提交了超 2400 项优化和修复&#xff0c;感谢每一…
阅读更多...
Ubuntu 22.04 桌面美化之Mac Big Sur风格

Ubuntu 22.04 桌面美化之Mac Big Sur风格

Ubuntu 默认的桌面也是一个不错的样式&#xff0c;但千篇一律的主题很容易让人疲惫。本文描述了如何通过安装 gnome 桌面主题和动画&#xff0c;使桌面趋向于 Mac 的样式。 美化后的样式如下&#xff0c;请参考&#xff1a; 一、主题和图标美化 1.1 安装 tweaks 打开终端&…
阅读更多...
抽奖小程序怎么做？

抽奖小程序怎么做？

抽奖小程序怎么做&#xff1f;大概需要多少钱&#xff1f; 价格方面&#xff0c;平台按年收费&#xff0c;一年1498至2498元。 明码标价&#xff0c;7天退款制度&#xff0c;随时退。 抽奖小程序怎么做步骤: 1.进入第三方抽奖小程序制作平台官网注册账号并登录。 抽奖小程…
阅读更多...
Kubernetes集群安装卸载

Kubernetes集群安装卸载

生命无罪&#xff0c;健康万岁&#xff0c;我是laity。 我曾七次鄙视自己的灵魂&#xff1a; 第一次&#xff0c;当它本可进取时&#xff0c;却故作谦卑&#xff1b; 第二次&#xff0c;当它在空虚时&#xff0c;用爱欲来填充&#xff1b; 第三次&#xff0c;在困难和容易之…
阅读更多...
银河麒麟服务器系统V10开启root用户自动登录的图文教程

银河麒麟服务器系统V10开启root用户自动登录的图文教程

HI，最近公司拿回来一个联想服务器，配置还可以啊，所以就想着在本地搭建一套常用的测试环境，但是这个服务器是扁平的，不像是主机那样，这种是锁定在主机箱上的，而且噪音很大，一直嗡嗡嗡的，所以打算弄好之后放在离我远一些的地方，不然真的没法工作，全是噪音，系统都部署…
阅读更多...
transformer14

transformer14

太强了都连载14了~~ 这次是无残差连接或归一化层&#xff0c;也能成功训练深度 尽管取得了很多显著的成就&#xff0c;但训练深度神经网络&#xff08;DNN&#xff09;的实践进展在很大程度上独立于理论依据。大多数成功的现代 DNN 依赖残差连接和归一化层的特定排列&#xff…
阅读更多...
ROS多机通信（ssh控制）

ROS多机通信（ssh控制）

这种方法需要在局域网范围内进行&#xff0c;通信距离取决于WIFI模块的传播距离 1、连接同局域网 将主机和从机连接相同的网络&#xff0c;在同一局域网内。例如192.168.0.*&#xff08;前三位相同&#xff09; 网络会自动给每个机器一个IP 2、安装SSH sudo apt-get insta…
阅读更多...
SpringBoot自动配置的原理-@SpringBootApplication

SpringBoot自动配置的原理-@SpringBootApplication

文章目录1自动配置原理1.1 SpringBootConfiguration1.2.ComponentScan1.3 EnableAutoConfiguration2 为什么不使用 Import 直接引入自动配置类学完这篇文章&#xff0c;可以了解到 SpringBoot 自动配置原理1自动配置原理 SpringBootConfiguration 是一个组合注解&#xff0c;由…
阅读更多...
Pinely Round 1 (Div. 1 + Div. 2) E.Make It Connected(思维题/并查集+分类讨论)

Pinely Round 1 (Div. 1 + Div. 2) E.Make It Connected(思维题/并查集+分类讨论)

题目 n(n<4e3)个点不包含自环和重边的无向图&#xff0c; 你可以执行以下操作若干次&#xff1a; 1. 选择一个点u 2. 对于每个点v(v≠u)来说&#xff0c;若u、v之间当前有一条边相连&#xff0c;则断开这条边&#xff0c; 否则在u、v之间加一条边&#xff0c;使之相连 …
阅读更多...
C++Mysql8.0数据库跨平台编程实战（下）

C++Mysql8.0数据库跨平台编程实战（下）

CMysql8.0数据库跨平台编程实战&#xff08;下&#xff09;第六章 跨平台中文乱码问题和mysql锁1、MySQLAPIC封装策略和方法说明windows上字符集gbk和utf8互转开始写代码把测试框架搭起来linux上字符集GBK和UTF8互转ZPMysql库添加字符集转换函数并测试GBK插入utf-8的数据我们把…
阅读更多...
Android之Zygote（下）--- SystemServer详解

Android之Zygote（下）--- SystemServer详解

SystemServer是由zygote.forkSystemServer函数fork出来的子进程&#xff0c;forkSystemServer是一个native函数&#xff0c; /dalvik/vm/native/dalvik_system_Zygote.c static void Dalvik_dalvik_system_Zygote_forkSystemServer(const u4* args, JValue* pResult) {pid_t …
阅读更多...
ABAP学习笔记之——第十章：面向对象ALV

ABAP学习笔记之——第十章：面向对象ALV

一、ALV ALV 是 ABAP List Viewer 的缩写&#xff0c;是实际业务中查询数据或修改数据时经常使用的程序。 1、ALV的主要功能排序功能 (Ascending/Descending); 过滤设置; 变更列宽; 变更布局; ABC 分析; 下载 Excel及 Word 文档的保存。 2、ALV的类型 Function ALV; …
阅读更多...
java计算机毕业设计ssm校园疫情防控系统u3669（附源码、数据库）

java计算机毕业设计ssm校园疫情防控系统u3669（附源码、数据库）

java计算机毕业设计ssm校园疫情防控系统u3669&#xff08;附源码、数据库&#xff09; 项目运行 环境配置&#xff1a; Jdk1.8 Tomcat8.5 Mysql HBuilderX&#xff08;Webstorm也行&#xff09; Eclispe&#xff08;IntelliJ IDEA,Eclispe,MyEclispe,Sts都支持&#xff0…
阅读更多...
Docker安装以及容器使用笔记

Docker安装以及容器使用笔记

我们知道容器是一个打包了应用和相关依赖的盒子，那怎么去操控这个盒子呢？ 这一篇我通过一个简单的aspnetcore程序来加深对盒子的理解，使用之前先 安装一下Docker的环境。 一：Docker的安装 官方下载地址：Install Docker Engine on CentOS | Docker Documentation ，跟着文…
阅读更多...
深度学习——NiN网络模型（笔记）

深度学习——NiN网络模型（笔记）

网络中的网络&#xff08;NiN&#xff09; 1.全连接层的问题&#xff1a;参数多&#xff0c;容易过拟合。 ①卷积层需要的参数较少 ②卷积层后第一个全连接层参数对比 参数过多带来的问题&#xff1a;1.占内存 2.占用计算的带宽多3.容易过拟合 2.NiN为了解决全连接层参数过多的…
阅读更多...
20221208英语学习

20221208英语学习

今日新词&#xff1a; fragment n.碎片&#xff0c;碎块&#xff0c;破片&#xff1b;片段 cynicism n.愤世嫉俗, 玩世不恭, (古希腊的)犬儒哲学, 冷言冷语, 犬儒学派 slight adj.少量的&#xff1b;轻微的&#xff1b;细小的&#xff1b;纤细的 willing adj.愿意, 乐意, 自…
阅读更多...
虚拟存储器

虚拟存储器

虚拟存储器 文章目录虚拟存储器虚拟存储器概述常规存储器管理方式的特征局部性原理虚拟存储器的定义和特征请求分页存储管理方式请求分页中的硬件支持请求分页中的内存分配页面调入策略页面置换算法最佳(Optimal)置换算法先进先出(FIFO)页面置换算法最近最久未使用(LRU)置换算法…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023