题面

[NOI2014] 随机数生成器 - 洛谷

题解

缝合题

第一部分，直接模拟题目操作生成二维数组即可，复杂度O(n*m+Q)

第二部分，是一个比较经典的字典序贪心

首先肯定需要将最小的数放到路径上，这样可选的剩下的数就被限制在了最小数的左上区间和右下区间

 

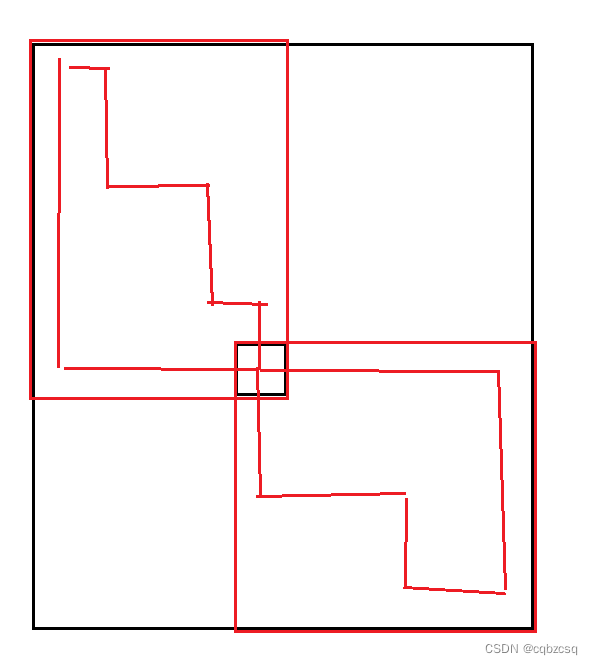
然后可以查询这两个区间的最小值，再分治下去？

然而查询操作需要依赖二维线段树或者其他数据结构，内存会爆掉

后来发现可以直接从小到大枚举所有的数，判定当前枚举到的数是不是在可行区间中就可以了

记录所有已经被选择的路径点，然后二分x，找到x最邻近的两个点，判断y是否在他们之间？

然而二分的时间复杂度也是过不了的

我们可以发现一个性质，对于每一行（每一列）来说，我们可以选择的路径一定是该行或者该列的一个区间

所以我们只需要更新这个区间就可以了

这样就变成了O（n）将一个点加入路径，O（1）判断一个点是否能被加入路径

一共只会将n+m-1个点加入路径，需要判断的有n*m个点

所以最终贪心的时间复杂度就是O(n*(n+m))

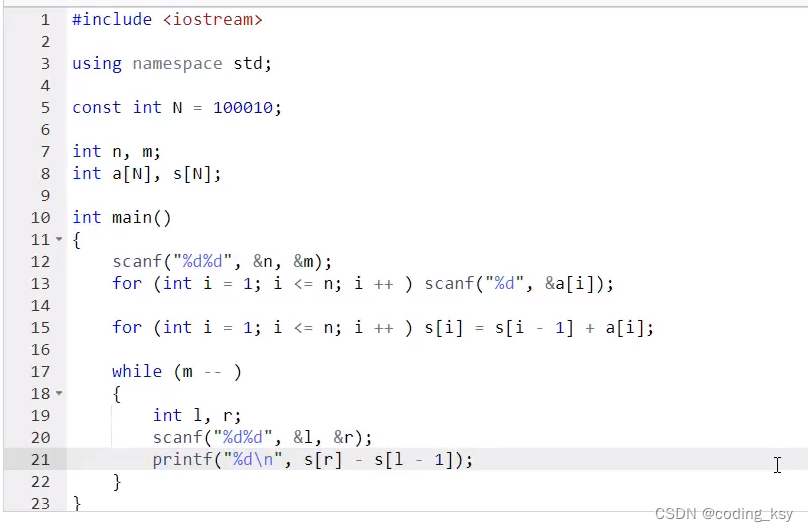
代码：

#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
#define N 5005
int a[N*N],pos[N*N];
int b[N][2];
int ans[2*N],acnt;
int main()
{
	int x,A,B,C,mod;
	int n,m,q,u,v;
	int i,j;
	scanf("%d%d%d%d%d",&x,&A,&B,&C,&mod);
	scanf("%d%d%d",&n,&m,&q);
	for(i=1;i<=n*m;i++){
		a[i]=i;
		x=(1ll*x*x%mod*A%mod+1ll*x*B%mod+C)%mod;
		swap(a[i],a[x%a[i]+1]);
	}
	for(i=1;i<=q;i++){
		scanf("%d%d",&u,&v);
		swap(a[u],a[v]);
	}
	for(i=1;i<=n*m;i++)
		pos[a[i]]=i;
	for(i=1;i<=n;i++){
		b[i][0]=1;
		b[i][1]=m;
	}
	for(i=1;i<=n*m;i++){
		int x=(pos[i]-1)/m+1;
		int y=(pos[i]-1)%m+1;
		if(b[x][0]<=y&&y<=b[x][1]){
			for(j=x-1;j>=1;j--){
				if(b[j][1]<=y)
					break;
				b[j][1]=y;
			}
			for(j=x+1;j<=n;j++){
				if(b[j][0]>=y)
					break;
				b[j][0]=y;
			}
			ans[++acnt]=i;
		}
	}
	sort(ans+1,ans+acnt+1);
	printf("%d",ans[1]);
	for(i=2;i<=acnt;i++)
		printf(" %d",ans[i]);
}