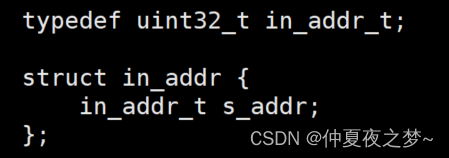
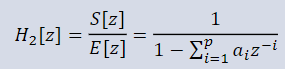核心思想
本文提出一种基于学习的组合求解器来实现图匹配。之前基于学习的图匹配方法都是利用神经网络提取特征构建关联矩阵,然后再利用可微分的Sinkhorn算法求解匹配矩阵。但本文提出的方法没有显式的构建关联矩阵和求解匹配矩阵的过程,而是将其转化成关联图(assignment graph),然后预测关联图中节点标签。整个编码解码和预测过程都是利用图神经网络实现的,充分利用了图强大的关联归纳偏好。
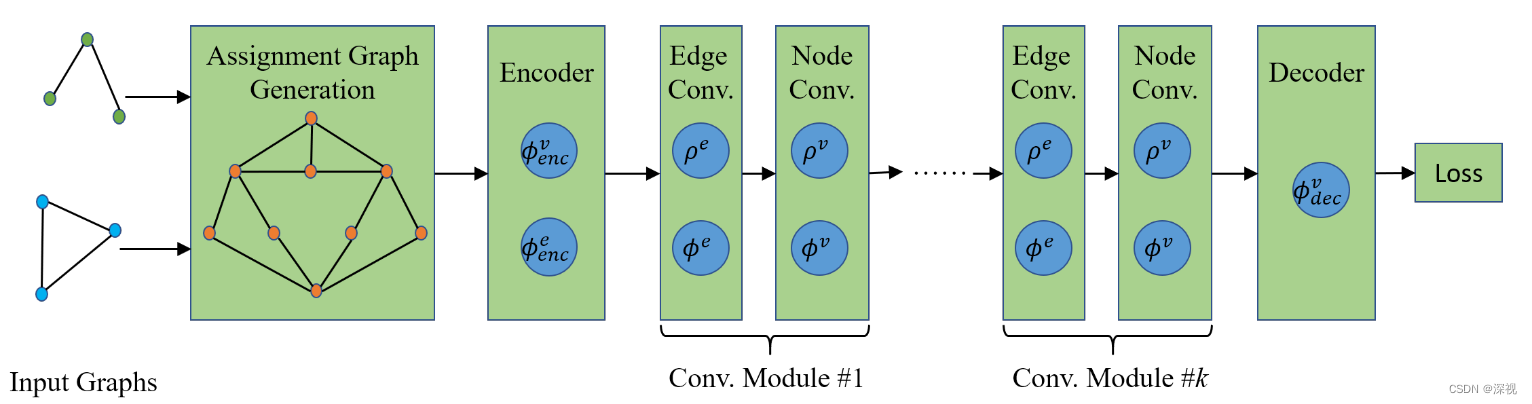
实现过程
首先介绍一下关联图的构建过程,在之前的博客中我们也曾经提到这一方法,我们这里再简要的回顾一下。如下图所示,我们有两个图
G
(
1
)
G^{(1)}
G(1)和
G
(
2
)
G^{(2)}
G(2),我们将其节点两两组合可以得到一个新的顶点集合,假设
G
(
1
)
G^{(1)}
G(1)和
G
(
2
)
G^{(2)}
G(2)的节点数量分别为
n
1
n_1
n1和
n
2
n_2
n2,那两两组合之后就会得到
n
1
×
n
2
n_1\times n_2
n1×n2个新的顶点。我们以新顶点
k
b
kb
kb和
i
a
ia
ia为例,如果原图
G
(
1
)
G^{(1)}
G(1)中节点
i
i
i和
k
k
k之间有边连接,且
G
(
2
)
G^{(2)}
G(2)中节点
a
a
a和
b
b
b之间有边连接,那么新图
G
A
G^{A}
GA中顶点
k
b
kb
kb和
i
a
ia
ia之间就有边连接,否则没有边。这样就构建出了新的关联图
G
A
G^{A}
GA。
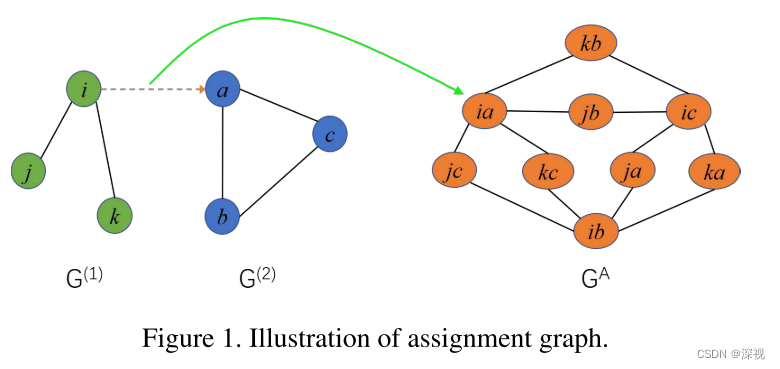
关联图的构建意义在于将原本预测点和点之间的匹配关系,转化成了预测关联图中顶点的标签。比如顶点
k
b
=
1
kb=1
kb=1,则表示节点
k
k
k和
b
b
b之间是匹配的。下面就来定义顶点和边的特征,方法也非常直接就将原图两个节点和两个边的特征级联起来,如下式
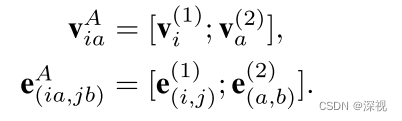
原图中节点的特征
v
i
v_i
vi是该节点的坐标,边的特征
e
(
i
,
j
)
e_{(i,j)}
e(i,j)是两个端点
v
i
,
v
j
v_i,v_j
vi,vj的坐标级联起来。与其他的基于深度学习的图匹配方法不同,本文提出的方法是不依赖CNN提取节点特征的,只需要坐标信息。这以为着该方法适用于各种类型的图之间的匹配问题。
得到关联图后,就是将关联图输入一个图神经网络进行编码解码和信息传递,最后进行顶点标签预测。作者采用两个多层感知机作为编码器
ϕ
e
n
c
v
\phi_{enc}^v
ϕencv和
ϕ
e
n
c
e
\phi_{enc}^e
ϕence,分别对节点和边的特征进行编码,将输入的关联图
G
A
G^{A}
GA变换成潜在表征
G
A
\mathbb{G}^A
GA。然后将
G
A
\mathbb{G}^A
GA输入到卷积模块中,这里的卷积模块与卷积神经网络不同,而是图神经网络的一种实现形式。它包括边卷积层和节点卷积层,边卷积层的操作如下
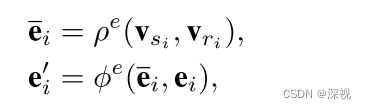
第一步是聚合边所连接的顶点的信息,
v
s
i
v_{s_i}
vsi和
v
r
i
v_{r_i}
vri分别表示边
e
i
e_i
ei所连接两个顶点的特征信息,特征聚合器
ρ
e
\rho^e
ρe计算方法如下
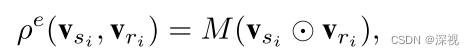
M
M
M表示参数矩阵,
⊙
\odot
⊙表示两个向量之间逐元素相乘。第二步是更新边的信息,
ϕ
e
\phi^e
ϕe表示一个多层感知机。节点卷积层实现过程如下
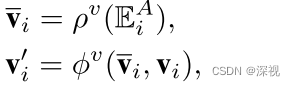
E
i
A
\mathbb{E}_i^A
EiA表示与节点
v
i
v_i
vi所有连接的边的特征集合,特征聚合器
ρ
v
\rho^v
ρv的计算方法如下
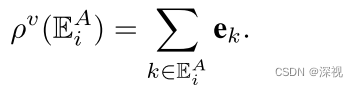
是一个无参数的累加过程。节点的更新器
ϕ
v
\phi^v
ϕv也是一个多层感知机。为什么称之为卷积模块呢?首先对于每一层网络而言,都只有一个对应的聚合器和更新器,也就是说对于各个顶点和边而言,他们的聚合器和更新器之间的权重是共享的,这就非常类似卷积神经网络中的卷积核的概念。每层网络的卷积核只有一个,依次对图像中的所有像素点进行卷积操作,而聚合器和更新器也是依次对所有的顶点和边进行操作。其次,因为聚合器只会聚合与当前节点相连的边或与边相连的顶点,但当多个卷积层叠加起来之后,第二层网络就可以聚合与当前顶点相隔一个顶点的其他顶点信息,也就是度为2的顶点。这个过程就非常类似卷积神经网络中的感受野,随着层数不断增加,感受野的范围也不断增大。正是基于上述的相似性,作者就称其为卷积模块,这里与图卷积神经网络GCN也是不同的概念,注意区分。
经过多个卷积模块处理后,需要对特征信息进行解码得到顶点标签的预测结果。解码器
ϕ
d
e
c
v
\phi_{dec}^v
ϕdecv同样是一个多层感知机,值得注意的是解码器指对节点特征进行处理,每个节点都会输出两个预测值,表示其匹配和不匹配的概率。最后计算损失,损失函数包含两个部分,第一个比较好理解就是一个二分类的交叉熵损失函数
L
p
e
r
m
L^{perm}
Lperm
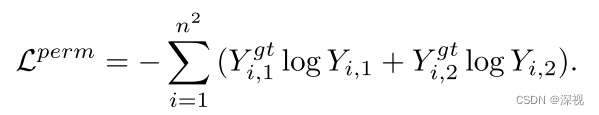
其中
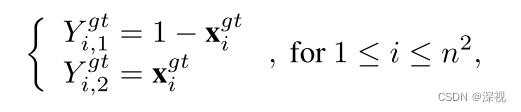
也就是说对于匹配的顶点,希望其对应的输出
Y
i
,
1
Y_{i,1}
Yi,1应该接近0,而
Y
i
,
2
Y_{i,2}
Yi,2接近1,不匹配的点反之。我们知道在图匹配领域中是有一一对应的约束的,也就是每个节点有且仅有一个匹配点。因此作者还增加了一个一一匹配的约束条件,实现方式如下
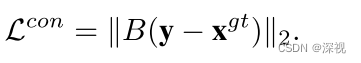
其中
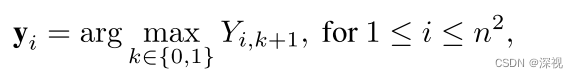
B
∈
{
0
,
1
}
2
n
×
n
2
B\in\{0,1\}^{2n\times n^2}
B∈{0,1}2n×n2,其满足以下条件
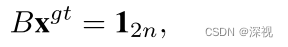
两个损失函数经过加权求和可得最终的损失
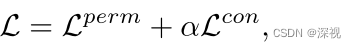
创新点
- 提出一种端到端的图匹配方法,将节点匹配问题转化为顶点预测问题
- 设计了一种卷积模块,用于聚合和更新关联图中顶点与边的特征信息
- 引入一一匹配的约束条件
算法评价
虽然关联图的设计思路在传统图匹配方法中就有过应用,本文是较早将其引入基于深度学习的图匹配领域的。卷积模块的设计非常巧妙,借鉴了卷积神经网络的思路,充分利用了图的结构信息。最终的输出的图每个节点都包含一个二维向量,我不太理解,为什么不设计为一个标量值,匹配程度越大,这个点的值越接近于1,这样不也可以实现分类的功能吗?可能是为了配合后面的一一匹配约束使用的?
如果大家对于深度学习与计算机视觉领域感兴趣,希望获得更多的知识分享与最新的论文解读,欢迎关注我的个人公众号“深视”。
![[附源码]计算机毕业设计常见Web漏洞对应PC应用系统Springboot程序](https://img-blog.csdnimg.cn/dd5be5cf2f784ed7ae4a5023f7aa6eb5.png)


![[附源码]计算机毕业设计贷款申请审核管理系统论文Springboot程序](https://img-blog.csdnimg.cn/f0a73885fe66475ba826e0f6c8ac4f3a.png)