以前的翻译文章，存档。翻译自：https://www.tomdalling.com/blog/modern-opengl/explaining-homogenous-coordinates-and-projective-geometry/， 有改动

在本文中，我将尽可能简单地解释齐次坐标(即4D坐标)。在之前的文章中，我们用了4D向量来做矩阵乘法，但是我从来没有真正定义过四维数。现在是时候近距离观察投影几何了。

术语

在使用3D技术的大多数时候，我们都在考虑欧几里得几何的关系——即三维空间中的坐标(X、Y、Z)。然而，在某些情况下，用投影几何学来思考是有用的。投影几何除了X、Y和Z之外有一个额外的维度，叫做W。这个四维空间称为“投影空间（projective space）”，投影空间中的坐标称为“齐次坐标（homogeneous coordinates）”。

不是四元数

四元数看起来很像齐次坐标。它们都是4D向量，通常表示为(X,Y,Z,W)。然而，四元数和齐次坐标是不同的概念，有不同的用途。

与2D的一个类比

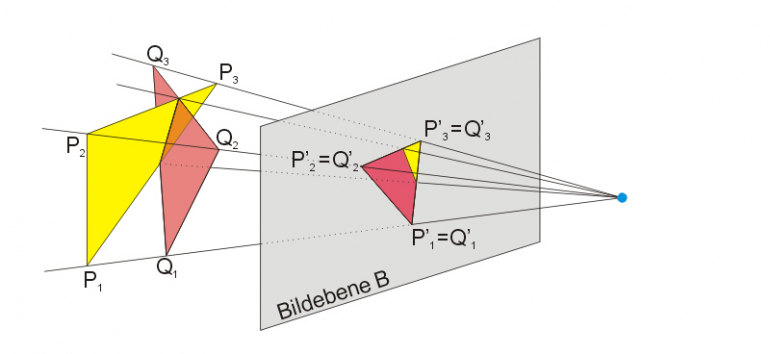
首先，让我们看看投影几何是如何在2D中工作的，然后再看3D。

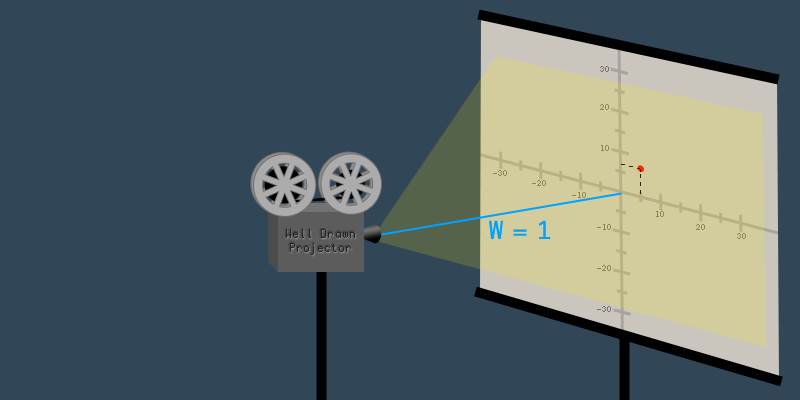
想象一个投影仪将二维图像投射到屏幕上。很容易看出投影图像的X和Y轴:

现在，如果你从这幅2D图像前后退一步，看向投影仪和屏幕，你就可以看到W维。W维是指从投影仪到屏幕的距离。

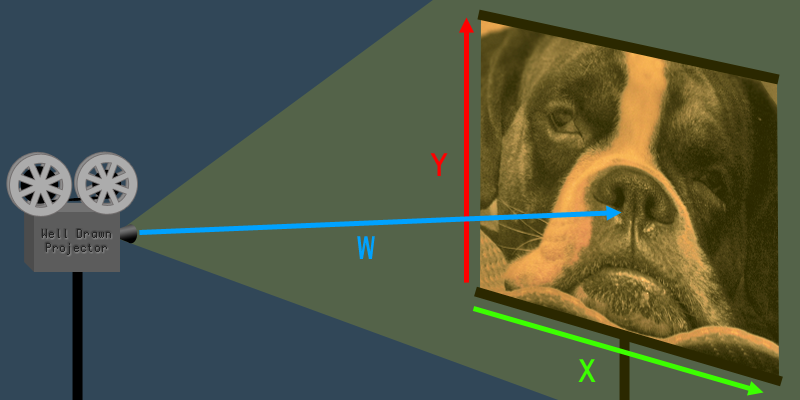
那么W维到底是做什么的呢？想象一下如果增加或减少W值——也就是说，如果增加或减少投影仪和屏幕之间的距离，二维图像会发生什么。如果你把投影仪靠近屏幕，整个2D图像就会变小。如果你把投影仪从屏幕移开，2D图像会变得更大。正如你所看到的，W的值影响图像的大小(也称为比例)。

应用于3D

目前还没有3D投影仪，所以很难想象3D的投影几何，但是W值的工作原理和2D是一样的。当W增加时，坐标放大。当W变小时，坐标缩小。W基本上是三维坐标的缩放变换。

当W = 1的时候

对于3D编程初学者通常的建议是，每当将3D坐标转换为4D坐标时，总是设置W=1。这样做的原因是当你把一个坐标缩放1倍时它不会收缩或放大，它会保持相同的大小。当W=1时它对X, Y, Z都没有影响。

因此，当涉及到3D计算机图形时，只有当W=1时，坐标才被认为是“正确的”。如果你用W>1表示坐标，那么所有东西看起来都太小了，而W< 1则所有东西看起来都太大了。如果你尝试用W=0渲染，当程序试图除以0时就会崩溃。在W< 0的情况下，所有的东西都会上下、前后颠倒的。

从数学上讲，不存在“不正确”的齐次坐标。使用W=1的坐标对于3D计算机图形来说只是一个有用的约定。

数学上

假设投影仪离屏幕3米远，在二维图像的坐标(15,21)处有一个点。这给出了投影坐标向量(X,Y,W)=(15,21,3)。

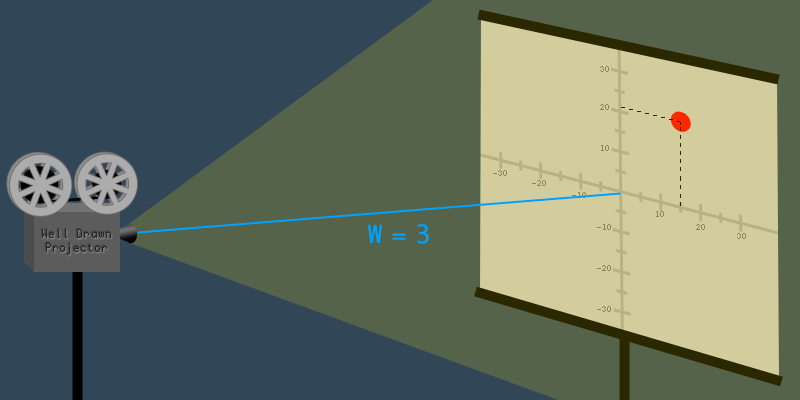
现在，假设投影仪被推得离屏幕更近，距离是1米。投影仪越接近屏幕，图像就越小。投影仪靠近了三倍，所以图像变小了三倍。如果取原来的坐标向量，把所有的值都除以3，就得到W=1的新向量:

$$(\frac{15}{3},\frac{21}{3},\frac{3}{3})=(5,7,1)$$

则点目前的坐标(5,7).

这就是“不正确的”齐次坐标如何转换成“正确的”坐标的方法:将所有的值除以w。

将一个向量中的所有值除以标量乘以除数的倒数。这里有一个4D的例子:

$$\frac{1}{5}(10,20,30,5)=(\frac{10}{5},\frac{20}{5},\frac{30}{5},\frac{5}{5})=(2,4,6,1)$$

使用GLM编写的c++示例如下:

glm::vec4 coordinate(10, 20, 30, 5);
glm::vec4 correctCoordinate = (1.0/coordinate.w) * coordinate;
//now, correctCoordinate == (2,4,6,1) 

齐次坐标在计算机图形学中的应用

如上所述，对于3D计算机图形，齐次坐标在某些情况下是有用的。我们来看看这里的一些情况。

3D坐标的平移矩阵

旋转和缩放变换矩阵只需要三列。但是，为了进行平移，矩阵至少需要有四列。这就是为什么变换通常是4x4矩阵。然而，由于矩阵乘法的规则，一个四列的矩阵不能与一个三维向量相乘。一个四列矩阵只能与一个四元向量相乘，这就是为什么我们经常使用齐次的4D向量而不是三维向量。

在矩阵变换中使用齐次坐标时，第四维W通常是不变的。当将一个三维坐标转换成一个四维坐标时，w要设置为1，并且在变换矩阵被应用之后，它通常仍然是1，在这一点上，它可以通过忽略W来转换回三维坐标。这适用于所有的平移、旋转和缩放转换，它们是到目前为止最常见的转换类型。值得注意的例外是投影矩阵，它确实影响W值。

透视变换

在3D技术中，“透视”是指物体在距离相机越远的地方越小的现象。如果猫离摄像机足够近的话，远处的山看起来可能比猫还小。

透视在三维计算机图形中是通过使用变换矩阵来实现的，变换矩阵可以改变每个顶点的W值。将摄像机矩阵应用到每个顶点后，在投影矩阵应用之前，每个顶点的Z值表示距离摄像机的距离。因此，Z越大，顶点的比例就越小。W值影响比例，所以投影矩阵只是根据Z值改变W值。这里有一个透视投影矩阵应用于齐次坐标的例子:

$$\left[\begin{array}{cccc}1& 0& 0& 0\\ 0& 1& 0& 0\\ 0& 0& 1& 0\\ 0& 0& 1& 0\end{array}\right]\left[\begin{array}{c}2\\ 3\\ 4\\ 1\end{array}\right]=\left[\begin{array}{c}2\\ 3\\ 4\\ 4\end{array}\right]$$

注意W值是如何从Z值变成4的。

应用透视投影矩阵后，每个顶点进行“透视分割”。透视图除法是将齐次坐标转换回W=1的一个特定术语，如本文前面所述。继续上面的例子，透视分割步骤如下:

$$\frac{1}{4}(2,3,4,4)=(0.5,0.75,1,1)$$

经过透视分割后，W值被丢弃，我们得到一个3D坐标，这就是根据3D透视投影被正确缩放的值。

在GLM中，这个透视投影矩阵可以使用GLM::perspective或GLM::frustum函数来创建。在老式的OpenGL中，它通常使用gluPerspective或gluFrustum函数创建。在OpenGL中，透视分割是在顶点着色器在每个顶点上运行之后自动发生的。这就是为什么gl_Position(顶点着色器的主要输出)是一个4D向量，而不是一个3D向量的原因之一。

放置方向光

齐次坐标的一个性质是它们允许你在无穷远(无限长度的向量)处有一点，这在三维坐标系中是不可能的。当W=0时，无穷远处的点就会出现。如果你试着把W=0齐次坐标转换成一个普通的W=1坐标，就会得到一系列的乘零运算:

$$\frac{1}{0}(2,3,4,0)=(\frac{2}{0},\frac{3}{0},\frac{4}{0},\frac{0}{0})$$

这意味着W=0的齐次坐标不能转换为三维坐标。

这个能有什么用呢？方向光可以是无限远的点光源。当一个点光源无限远时，光线就会变得平行，所有的光都沿着一个方向传播。这就是方向光的定义。

所以传统上，在3D图形中，方向光与点光源的区别在于光源位置向量中W的值。如果W=1，那么它就是点光源。如果W=0，那么它就是一个方向光。

这更像是一种传统约定，而不是编写光照代码的有用方法。方向光和点光源通常用单独的代码实现，因为它们的行为不同。一个典型的光照着色器可能看起来是这样的:

if(lightPosition.w == 0.0){
    //directional light code here
} else {
    //point light code here
}

总结

齐次坐标有一个额外的维度W，它可以缩放X，Y和Z的值。用于平移和透视投影变换的矩阵只能应用于齐次坐标，这就是为什么它们在3D计算机图形中如此常见。当W=1时，X、Y和Z值被认为是“正确的”。任何齐次坐标都可以通过四维数除以W值来转换为W=1，除非W=0。当W=0时，坐标表示无穷远处的点(一个无限长的矢量)，这通常用来表示方向光的方向。