1.什么是Attention

所谓Attention机制，便是聚焦于局部信息的机制，比如图像中的某一个图像区域。随着任务的变化，注意力区域往往会发生变化。

面对上面这样的一张图，如果你只是从整体来看，只看到了很多人头，但是你拉近一个一个仔细看就了不得了，都是天才科学家。

图中除了人脸之外的信息其实都是无用的，也做不了什么任务，Attention机制便是要找到这些最有用的信息，可以想见最简单的场景就是从照片中检测人脸了。

注意力机制的核心重点就是让网络关注到它更需要关注的地方。

当我们使用卷积神经网络去处理图片的时候，我们会更希望卷积神经网络去注意应该注意的地方，而不是什么都关注，我们不可能手动去调节需要注意的地方，这个时候，如何让卷积神经网络去自适应的注意重要的物体变得极为重要。

注意力机制就是实现网络自适应注意的一个方式。

一般而言，注意力机制可以分为通道注意力机制，空间注意力机制，以及二者的结合。

2.注意力机制的实现方式

2.1 SENet的实现

SENet是通道注意力机制的典型实现，其具体实现方式就是：

1、对输入进来的特征层进行全局平均池化。

2、然后进行两次全连接，第一次全连接神经元个数较少，第二次全连接神经元个数和输入特征层相同。

3、在完成两次全连接后，我们再取一次Sigmoid将值固定到0-1之间，此时我们获得了输入特征层每一个通道的权值（0-1之间）。

4、在获得这个权值后，我们将这个权值乘上原输入特征层即可。

实现代码如下：

import torch
import torch.nn as nn
import math

class se_block(nn.Module):
    def __init__(self, channel, ratio=16):
        super(se_block, self).__init__()
        self.avg_pool = nn.AdaptiveAvgPool2d(1)
        self.fc = nn.Sequential(
                nn.Linear(channel, channel // ratio, bias=False),
                nn.ReLU(inplace=True),
                nn.Linear(channel // ratio, channel, bias=False),
                nn.Sigmoid()
        )

    def forward(self, x):
        b, c, _, _ = x.size()
        y = self.avg_pool(x).view(b, c)
        y = self.fc(y).view(b, c, 1, 1)
        return x * y

2.2 CBAM实现

CBAM将通道注意力机制和空间注意力机制进行一个结合，相比于SENet只关注通道的注意力机制可以取得更好的效果。其实现示意图如下所示，CBAM会对输入进来的特征层，分别进行通道注意力机制的处理和空间注意力机制的处理。

下图是通道注意力机制和空间注意力机制的具体实现方式：

图像的上半部分为通道注意力机制，通道注意力机制的实现可以分为两个部分，我们会对输入进来的单个特征层，分别进行全局平均池化和全局最大池化。之后对平均池化和最大池化的结果，利用共享的全连接层进行处理，我们会对处理后的两个结果进行相加，然后取一个sigmoid，此时我们获得了输入特征层每一个通道的权值（0-1之间）。在获得这个权值后，我们将这个权值乘上原输入特征层即可。

图像的下半部分为空间注意力机制，我们会对输入进来的特征层，在每一个特征点的通道上取最大值和平均值。之后将这两个结果进行一个堆叠，利用一次通道数为1的卷积调整通道数，然后取一个sigmoid，此时我们获得了输入特征层每一个特征点的权值（0-1之间）。在获得这个权值后，我们将这个权值乘上原输入特征层即可。

具体实现：

class ChannelAttention(nn.Module):
    def __init__(self, in_planes, ratio=8):
        super(ChannelAttention, self).__init__()
        self.avg_pool = nn.AdaptiveAvgPool2d(1)
        self.max_pool = nn.AdaptiveMaxPool2d(1)

        # 利用1x1卷积代替全连接
        self.fc1   = nn.Conv2d(in_planes, in_planes // ratio, 1, bias=False)
        self.relu1 = nn.ReLU()
        self.fc2   = nn.Conv2d(in_planes // ratio, in_planes, 1, bias=False)

        self.sigmoid = nn.Sigmoid()

    def forward(self, x):
        avg_out = self.fc2(self.relu1(self.fc1(self.avg_pool(x))))
        max_out = self.fc2(self.relu1(self.fc1(self.max_pool(x))))
        out = avg_out + max_out
        return self.sigmoid(out)

class SpatialAttention(nn.Module):
    def __init__(self, kernel_size=7):
        super(SpatialAttention, self).__init__()

        assert kernel_size in (3, 7), 'kernel size must be 3 or 7'
        padding = 3 if kernel_size == 7 else 1
        self.conv1 = nn.Conv2d(2, 1, kernel_size, padding=padding, bias=False)
        self.sigmoid = nn.Sigmoid()

    def forward(self, x):
        avg_out = torch.mean(x, dim=1, keepdim=True)
        max_out, _ = torch.max(x, dim=1, keepdim=True)
        x = torch.cat([avg_out, max_out], dim=1)
        x = self.conv1(x)
        return self.sigmoid(x)

class cbam_block(nn.Module):
    def __init__(self, channel, ratio=8, kernel_size=7):
        super(cbam_block, self).__init__()
        self.channelattention = ChannelAttention(channel, ratio=ratio)
        self.spatialattention = SpatialAttention(kernel_size=kernel_size)

    def forward(self, x):
        x = x * self.channelattention(x)
        x = x * self.spatialattention(x)
        return x

2.3 ECA的实现

ECANet是也是通道注意力机制的一种实现形式。ECANet可以看作是SENet的改进版。
ECANet的作者认为SENet对通道注意力机制的预测带来了副作用，捕获所有通道的依赖关系是低效并且是不必要的。
在ECANet的论文中，作者认为卷积具有良好的跨通道信息获取能力。

ECA模块的思想是非常简单的，它去除了原来SE模块中的全连接层，直接在全局平均池化之后的特征上通过一个1D卷积进行学习。

当我们使用 1D 卷积时，通常会将卷积核应用于输入序列的每个位置，从而生成一个输出序列。下面是一个简单的例子，假设我们有一个长度为 10 的 1D 张量 $x$，卷积核的大小为 3，步幅为 1，填充方式为“VALID”，即不进行填充。卷积核权重如下：

$$W=\left[\begin{array}{ccc}1& -1& 0.5\end{array}\right]$$

那么，我们可以通过以下方式对输入张量进行 1D 卷积运算：

1. 将卷积核从左到右滑动，每次移动一个位置，与输入张量的一部分进行卷积运算。

2. 将卷积得到的结果存储在输出张量的相应位置。

3. 重复步骤 1 和 2，直到卷积核滑动到输入张量的末尾。

具体来说，我们可以使用如下的方式来计算输出张量中的每个元素：

$$y_i=\sum _{j=0}^2{W}_j{x}_{i+j}$$

其中，$y_i$ 是输出张量中的第 $i$ 个元素，$W_j$ 是卷积核的第 $j$ 个权重，$x_{i+j}$ 是输入张量中的第 $i+j$ 个元素。注意，由于我们使用“VALID”填充方式，因此输入张量的边缘元素不会被卷积核考虑。

下面是一个简单的 Python 代码示例，演示如何使用 PyTorch 实现 1D 卷积运算：

import torch
import torch.nn as nn

# 定义输入张量
x = torch.tensor([1, 2, 3, 4, 5, 6, 7, 8, 9, 10], dtype=torch.float32).unsqueeze(0).unsqueeze(0)
# 将输入张量转为 1D 卷积层的输入格式：[batch_size, in_channels, sequence_length]

# 定义卷积核
conv = nn.Conv1d(in_channels=1, out_channels=1, kernel_size=3, stride=1, padding=0, bias=False)
conv.weight.data = torch.tensor([[[1, -1, 0.5]]], dtype=torch.float32)

# 进行 1D 卷积运算
y = conv(x)

# 输出结果
print(y)

运行结果如下：

tensor([[[0.5000, 1.0000, 1.5000, 2.0000, 2.5000, 3.0000, 3.5000, 4.0000]]],
       grad_fn=<ConvolutionBackward0>)

可以看到，输出张量中的每个元素都是通过卷积核与输入张量进行卷积运算得到的。这就是一个简单的 1D 卷积的例子，它可以应用于时间序列数据、文本数据等领域。

如下图所示，左图是常规的SE模块，右图是ECA模块。ECA模块用1D卷积替换两次全连接。

原文链接：https://blog.csdn.net/weixin_44791964/article/details/121371986

具体代码实现：

import torch
import torch.nn as nn

class eca_block(nn.Module):
    def __init__(self, channel, b=1, gamma=2):
        super(eca_block, self).__init__()
        kernel_size = int(abs((math.log(channel, 2) + b) / gamma))
        kernel_size = kernel_size if kernel_size % 2 else kernel_size + 1
        
        self.avg_pool = nn.AdaptiveAvgPool2d(1)
        self.conv = nn.Conv1d(1, 1, kernel_size=kernel_size, padding=(kernel_size - 1) // 2, bias=False) 
        self.sigmoid = nn.Sigmoid()

    def forward(self, x):
        y = self.avg_pool(x)
        y = self.conv(y.squeeze(-1).transpose(-1, -2)).transpose(-1, -2).unsqueeze(-1)
        y = self.sigmoid(y)
        return x * y.expand_as(x)

3.自注意力实现

3.1 Self-Attention中QKV的理解

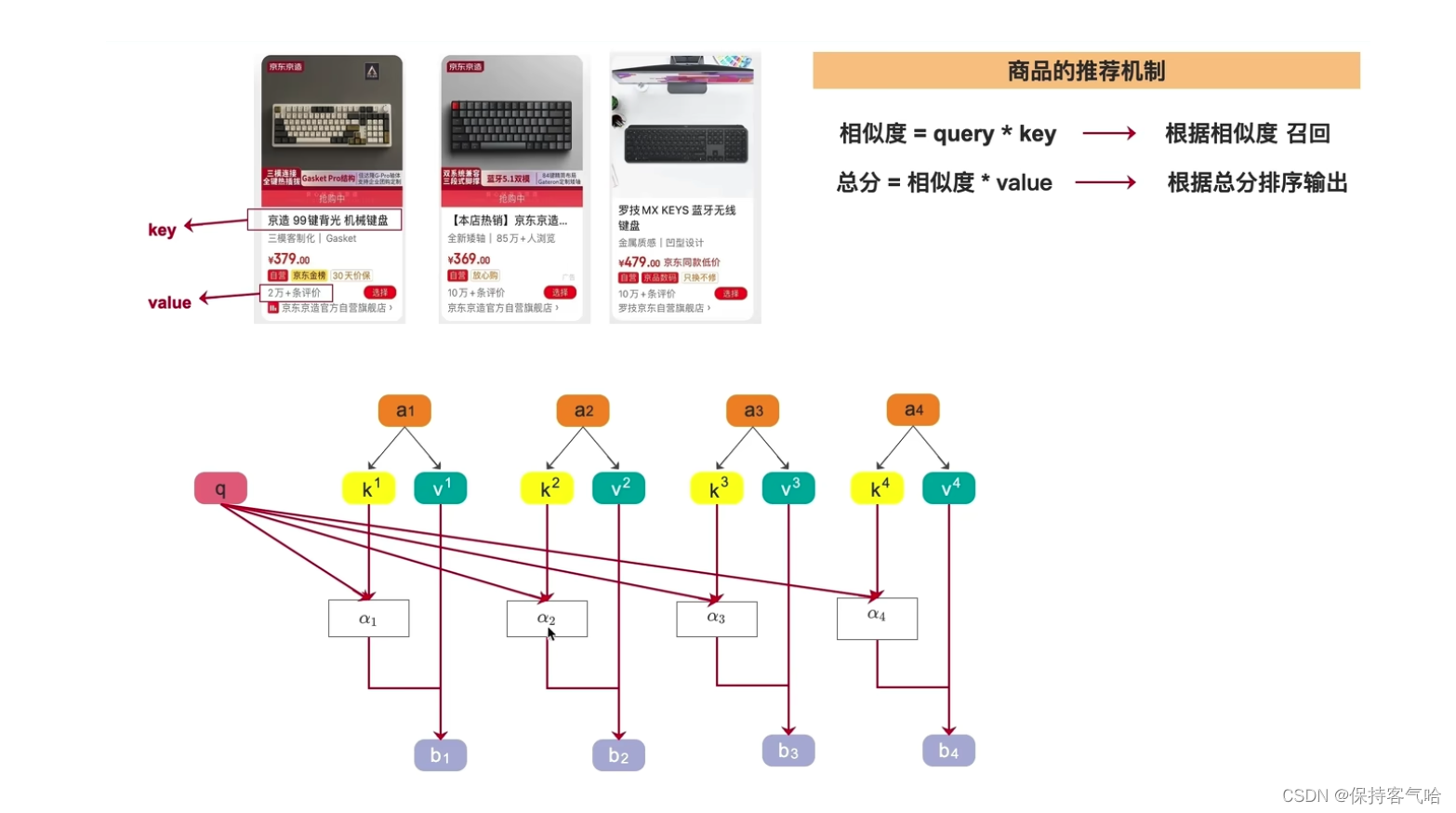
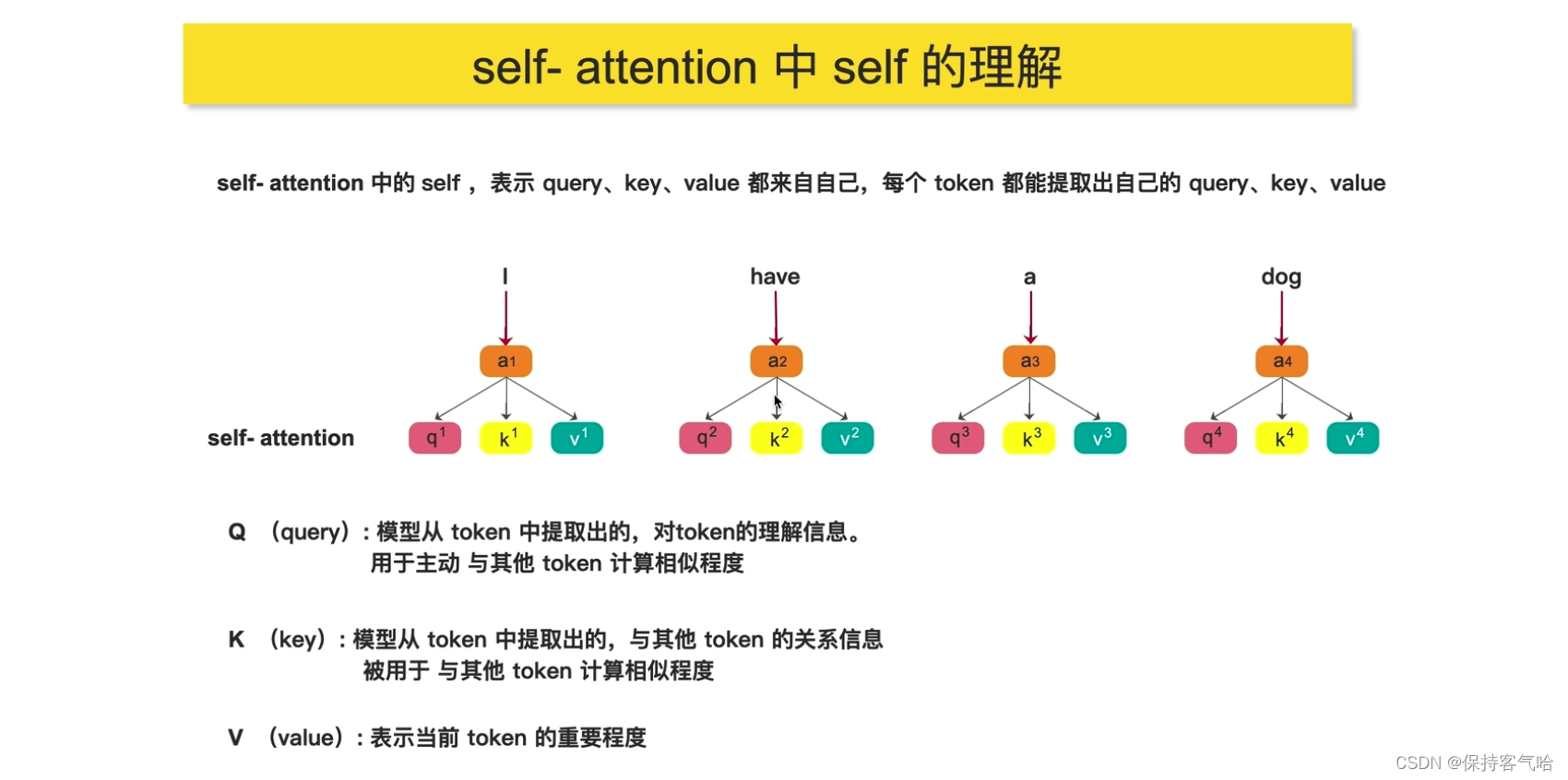
3.2 Self-attention 中self的理解

3.3 Self- attention中的计算过程

原文链接：https://blog.csdn.net/qq_37541097/article/details/117691873

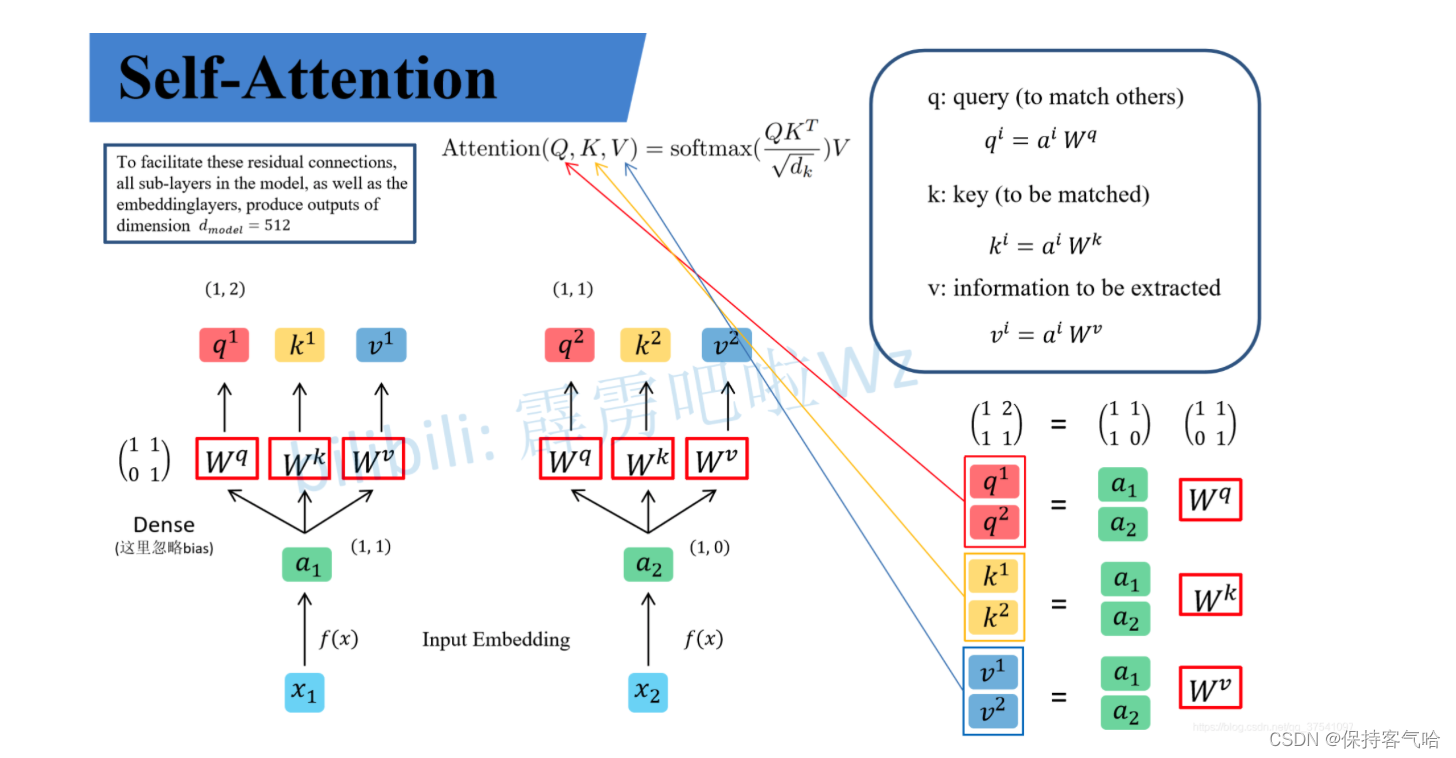
假设输入的序列长度为2，输入就两个节点$x_1$,$x_2$,然后通过Input Embedding也就是图中的f(x)将输入映射到$a_1 , a_2 $紧接着分别将 $a_1 , a_2 $分别通过三个变换矩阵$W_q , W_k , W_v$ （这三个参数是可训练的，是共享的）得到对应的$q^i,k^i,v^i$
（这里在源码中是直接使用全连接层实现的，这里为了方便理解，忽略偏执）

• q代表query，后续会与每一个k进行匹配；

• k代表key，后续会被每个q匹配；

• v代表从a中提取得到的信息。

• 后续q和k匹配的过程可以理解成计算两者的相关性，相关性越大对应v的权重也就越大。

假设$a_1=(1,1)，a_2=(1,0)$，$W^q=\left(\begin{array}{cc}1& 1\\ 0& 1\end{array}\right)$。那么：

$q^1=(1,1)\left(\begin{array}{cc}1& 1\\ 0& 1\end{array}\right)=(1,2)$

$q^2=(1,0)\left(\begin{array}{cc}1& 1\\ 0& 1\end{array}\right)=(1,1)$

前面有说Transformer是可以并行化的，所以可以直接写成：

$\left(\begin{array}{c}{q}^1\\ q^2\end{array}\right)=\left(\begin{array}{cc}1& 1\\ 1& 0\end{array}\right)\left(\begin{array}{cc}1& 1\\ 0& 1\end{array}\right)=\left(\begin{array}{cc}1& 2\\ 1& 1\end{array}\right)$

同理我们可以得到$\left(\begin{array}{c}{k}^1\\ k^2\end{array}\right)$和$\left(\begin{array}{c}{v}^1\\ v^2\end{array}\right)$，那么求得的$\left(\begin{array}{c}{q}^1\\ q^2\end{array}\right)$就是原论文中的Q，$\left(\begin{array}{c}{k}^1\\ k^2\end{array}\right)$就是K，$\left(\begin{array}{c}{v}^1\\ v^2\end{array}\right)$就是V。

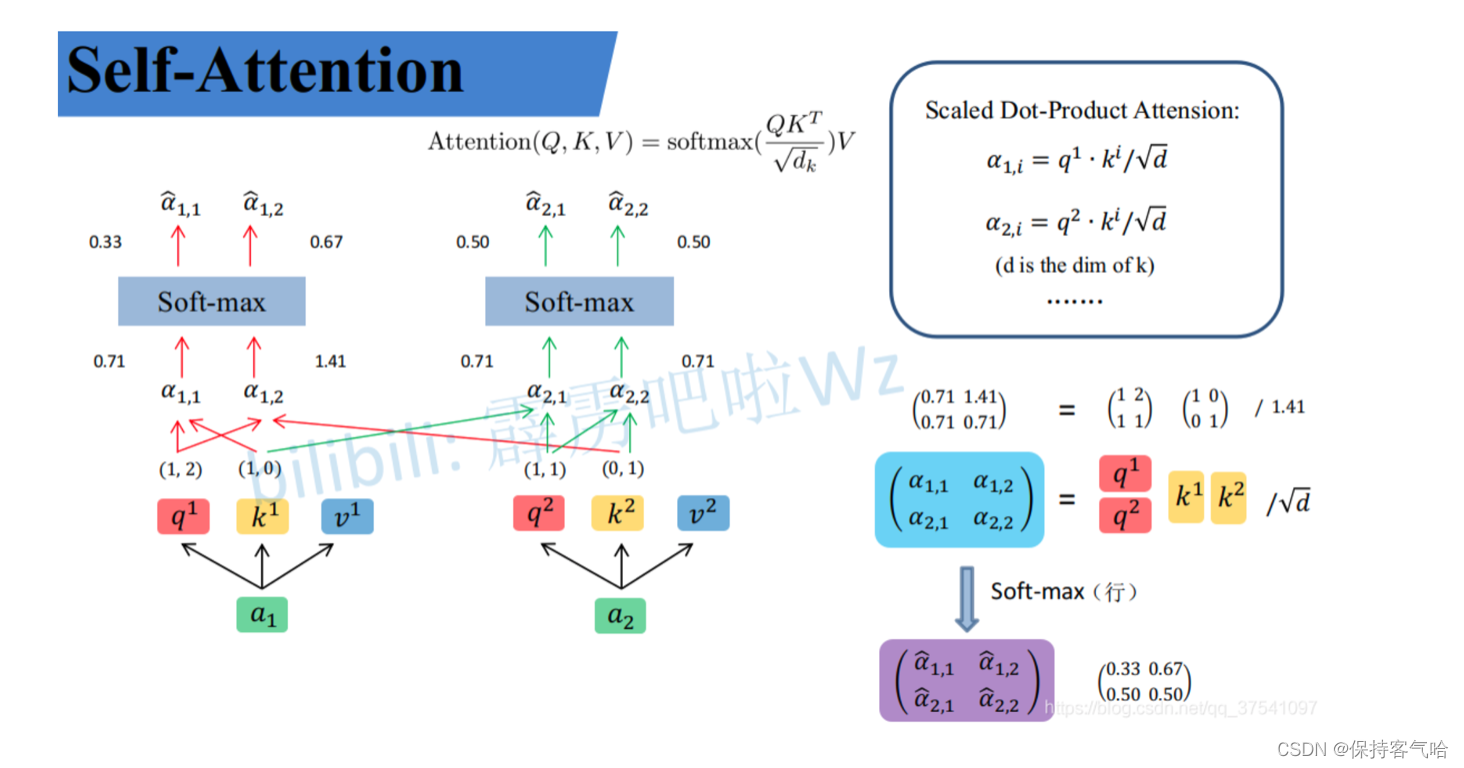
接着先拿$q^1$去匹配每个k，点乘操作，接着除以得$\sqrt{d}$到对应的α，其中$d$代表向量$k^i$的长度，在本示例中等于2，除以$d$的原因在论文中的解释是“进行点乘后的数值很大，导致通过softmax后梯度变的很小”，所以通过除以$\sqrt{d}$来进行缩放。

比如计算${\alpha }_{1,i}$：

$${\alpha }_{1,1}=q^1\cdot k^1/\sqrt{d}=1\times 1+2\times 0/2=0.71$$

$${\alpha }_{1,2}=q^1\cdot k^2/d=1\times 0+2\times 1/2=1.41$$

同理拿$q^2$去匹配所有的k能得到${\alpha }_{2,i}$，统一写成矩阵乘法形式：

$$\left(\begin{array}{cc}{\alpha }_{1,1}& {\alpha }_{1,2}\\ {\alpha }_{2,1}& {\alpha }_{2,2}\end{array}\right)=\frac{\left(\begin{array}{c}{q}^1\\ q^2\end{array}\right)\left(\begin{array}{cc}{k}^1& k^2\end{array}\right)}{\sqrt{d}}$$

接着对每一行即$({\alpha }_{1,1},{\alpha }_{1,2})和({\alpha }_{2,1},{\alpha }_{2,2})$分别进行softmax处理得到$({\hat{\alpha }}_{1,1},{\hat{\alpha }}_{1,2})$和$({\hat{\alpha }}_{2,1},{\hat{\alpha }}_{2,2})$，这里的$\hat{a}$相当于计算得到针对每个v的权重。到这我们就完成了Attention(Q, K, V)公式中$softmax(Q{K}^T/\sqrt{d_k})$部分。

上面已经计算得到α，即针对每个v的权重，接着进行加权得到最终结果：
$$\begin{array}{rl}{b}_1& ={\hat{\alpha }}_{1,1}\times v^1+{\hat{\alpha }}_{1,2}\times v^2=(0.33,0.67),b_2={\hat{\alpha }}_{2,1}\times v^1+{\hat{\alpha }}_{2,2}\times v^2=(0.50,0.50)\end{array}$$

统一写成矩阵乘法形式：
$$\left(\begin{array}{c}{b}_1\\ b_2\end{array}\right)=\left(\begin{array}{cc}{\hat{\alpha }}_{1,1}& {\hat{\alpha }}_{1,2}\\ {\hat{\alpha }}_{2,1}& {\hat{\alpha }}_{2,2}\end{array}\right)\left(\begin{array}{c}{v}^1\\ v^2\end{array}\right)$$
到这，Self-Attention的内容就讲完了。总结下来就是论文中的一个公式：

$$Attention(Q,K,V)=softmax(\frac{Q{K}^T}{\sqrt{d_k}})V$$

其中，Q、K、V是通过输入的序列计算得到的，softmax函数用于计算每个位置对应的权重，最终的输出是V的加权和，权重即softmax函数的输出。这个公式是Transformer模型的核心组成部分，被广泛应用于自然语言处理和其他序列数据处理任务中。

import torch
import torch.nn as nn


class Self_Attention(nn.Module):
    def __init__(self, dim, dk, dv):
        super(Self_Attention, self).__init__()
        self.scale = dk ** -0.5  # 公式里的根号dk
        self.q = nn.Linear(dim, dk)
        self.k = nn.Linear(dim, dk)
        self.v = nn.Linear(dim, dv)  # v的维度不需要和q，k一样

    def forward(self, x):
        q = self.q(x)
        k = self.k(x)
        v = self.v(x)

        attn = (q @ k.transpose(-2, -1)) * self.scale
        attn = attn.softmax(dim = -1)

        x = attn @ v

        return x

att = Self_Attention(dim=2, dk=2, dv=3)
x = torch.rand((1, 4, 2))  # 1 是batch_size 4是token数量 2是每个token的长度
print(x)
output = att(x)

3.4 Muti-Head Attention

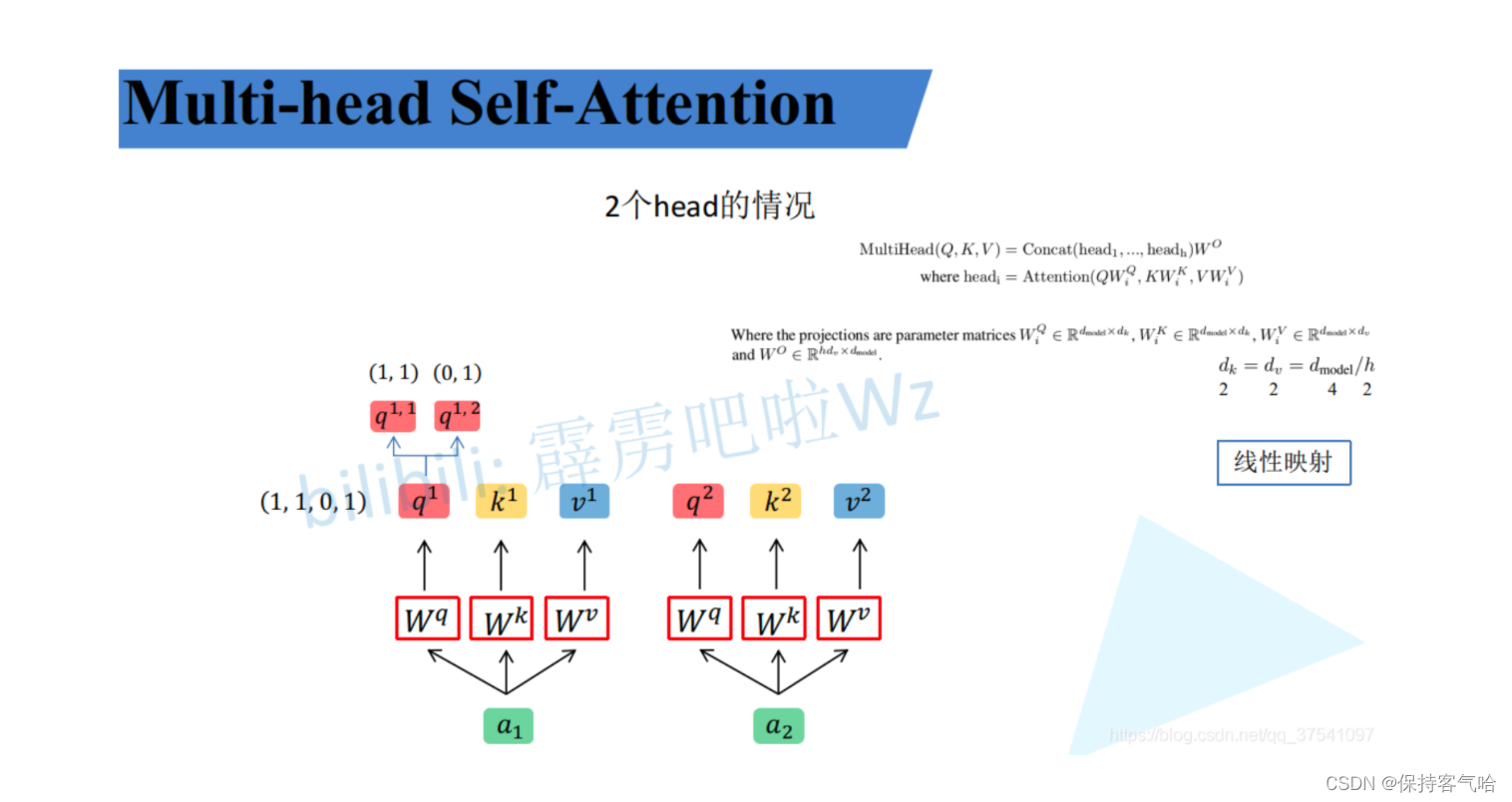
首先还是和Self-Attention模块一样将$a_i$分别通过$W^q$、$W^k$、$W^v$得到对应的$q^i$、$k^i$、$v^i$，然后再根据使用的head的数目$h$进一步把得到的$q^i$、$k^i$、$v^i$均分成$h$份。比如下图中假设$h=2$，然后$q^1$拆分成$q^{1,1}$和$q^{1,2}$，那么$q^{1,1}$就属于head1，$q^{1,2}$属于head2。

看到这里，如果读过原论文的人肯定有疑问，论文中不是写的通过$W_i^Q$、$W_i^K$、$W_i^V$映射得到每个head的$Q_i$、$K_i$、$V_i$吗：

$$hea{d}_i=\mathrm{Attention}(Q{W}_i^Q,K{W}_i^K,V{W}_i^V)$$

但我在GitHub上看到一些源代码中简单地进行了均分，其实也可以将$W_i^Q$、$W_i^K$、$W_i^V$设置为对应的值来实现均分，比如下图中的$Q$通过$W_1^Q$就能得到均分后的$Q_1$。

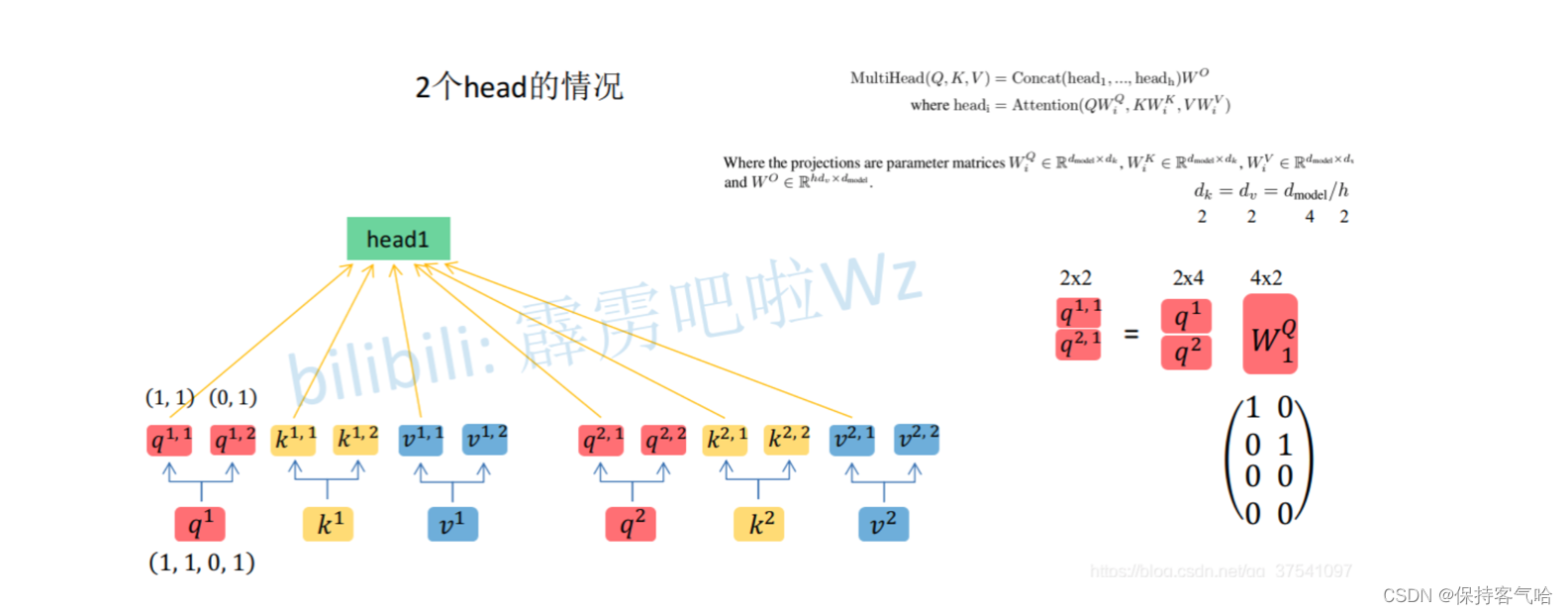
通过上述方法就能得到每个$hea{d}_i$对应的$Q_i$、$K_i$、$V_i$参数，接下来针对每个head使用和Self-Attention中相同的方法即可得到对应的结果。

$$\mathrm{Attention}(Q_i,K_i,V_i)=\mathrm{softmax}(\frac{Q_i{K}_i^T}{\sqrt{d_k}})V_i$$

其中，$Q_i$、$K_i$、$V_i$是通过输入序列计算得到的，softmax函数用于计算每个位置对应的权重，最终的输出是$V_i$的加权和，权重即softmax函数的输出。

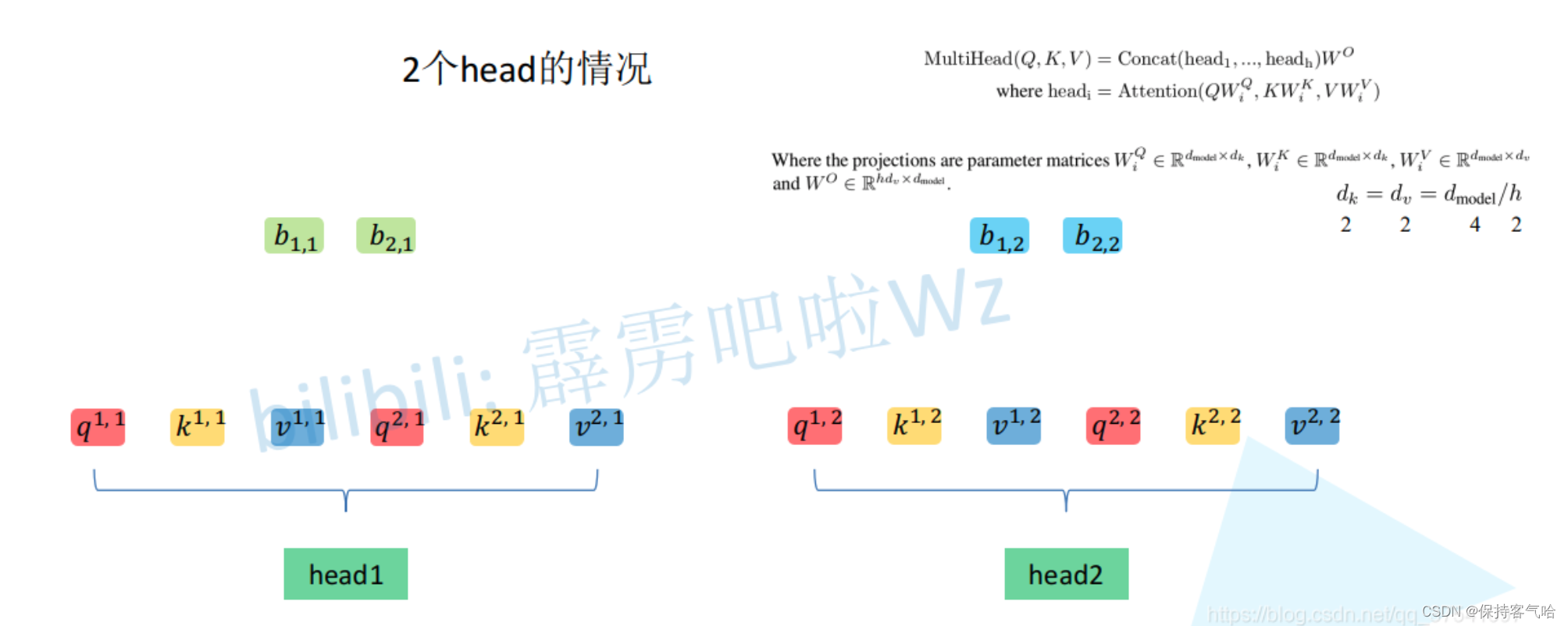
接着将每个head得到的结果进行concat拼接，比如下图中$b_{1,1}$（$hea{d}_1$得到的$b_1$）和$b_{1,2}$（$hea{d}_2$得到的$b_1$）拼接在一起，$b_{2,1}$（$hea{d}_1$得到的$b_2$）和$b_{2,2}$（$hea{d}_2$得到的$b_2$）拼接在一起。

接着将拼接后的结果通过$W^O$（可学习的参数）进行融合，如下图所示，融合后得到最终的结果$b_1,b_2$。

代码实现：

import torch  # 导入PyTorch库
import torch.nn as nn


class MultiHeadAttention(nn.Module):
    def __init__(self, n_heads, d_model, dropout=0.1):
        super(MultiHeadAttention, self).__init__()  # 继承自nn.Module基类
        self.n_heads = n_heads  # 多头注意力头数
        self.d_model = d_model  # 输入向量维度
        self.d_k = d_model // n_heads  # 每个头的维度
        self.dropout = nn.Dropout(p=dropout)  # dropout概率

        # 初始化Query、Key、Value的权重矩阵
        self.W_q = nn.Linear(d_model, n_heads * self.d_k)  # Query权重矩阵
        self.W_k = nn.Linear(d_model, n_heads * self.d_k)  # Key权重矩阵
        self.W_v = nn.Linear(d_model, n_heads * self.d_k)  # Value权重矩阵

        # 初始化输出的权重矩阵
        self.W_o = nn.Linear(n_heads * self.d_k, d_model)  # 输出向量的权重矩阵

    def forward(self, x, mask=None):
        # 输入 x 的维度为 [batch_size, seq_len, d_model]
        batch_size, seq_len, d_model = x.size()

        # 通过权重矩阵计算 Q、K、V
        Q = self.W_q(x).view(batch_size, seq_len, self.n_heads, self.d_k)
        K = self.W_k(x).view(batch_size, seq_len, self.n_heads, self.d_k)
        V = self.W_v(x).view(batch_size, seq_len, self.n_heads, self.d_k)

        # 交换维度以便于计算注意力权重
        Q = Q.permute(0, 2, 1, 3).contiguous().view(batch_size * self.n_heads, seq_len, self.d_k)
        K = K.permute(0, 2, 1, 3).contiguous().view(batch_size * self.n_heads, seq_len, self.d_k)
        V = V.permute(0, 2, 1, 3).contiguous().view(batch_size * self.n_heads, seq_len, self.d_k)

        # 计算注意力权重
        scores = torch.bmm(Q, K.transpose(1, 2)) / torch.sqrt(torch.tensor(self.d_k, dtype=torch.float))
        if mask is not None:
            scores = scores.masked_fill(mask == 0, -1e9)
        attn_weights = nn.Softmax(dim=-1)(scores)
        attn_weights = self.dropout(attn_weights)

        # 计算输出向量
        attn_output = torch.bmm(attn_weights, V)
        attn_output = attn_output.view(batch_size, self.n_heads, seq_len, self.d_k)
        attn_output = attn_output.permute(0, 2, 1, 3).contiguous().view(batch_size, seq_len,
                                                                        self.n_heads * self.d_k)
        output = self.W_o(attn_output)

        return output


# 定义输入向量
x = torch.randn(2, 10, 128)

# 定义注意力模块
attn = MultiHeadAttention(n_heads=8, d_model=128)

# 进行前向传播计算
output = attn(x)

# 打印输出向量的形状
print(output.shape)  # 输出：torch.Size([2, 10, 128])

4. Vision Transformer

Vision Transformer(ViT)是一种基于Transformer的图像分类模型。下图是原论文中给出的ViT模型框架。

简单而言，ViT模型由三个模块组成：

• Linear Projection of Flattened Patches(Embedding层)
• Transformer Encoder(图右侧有给出更加详细的结构)
• MLP Head（最终用于分类的层结构）

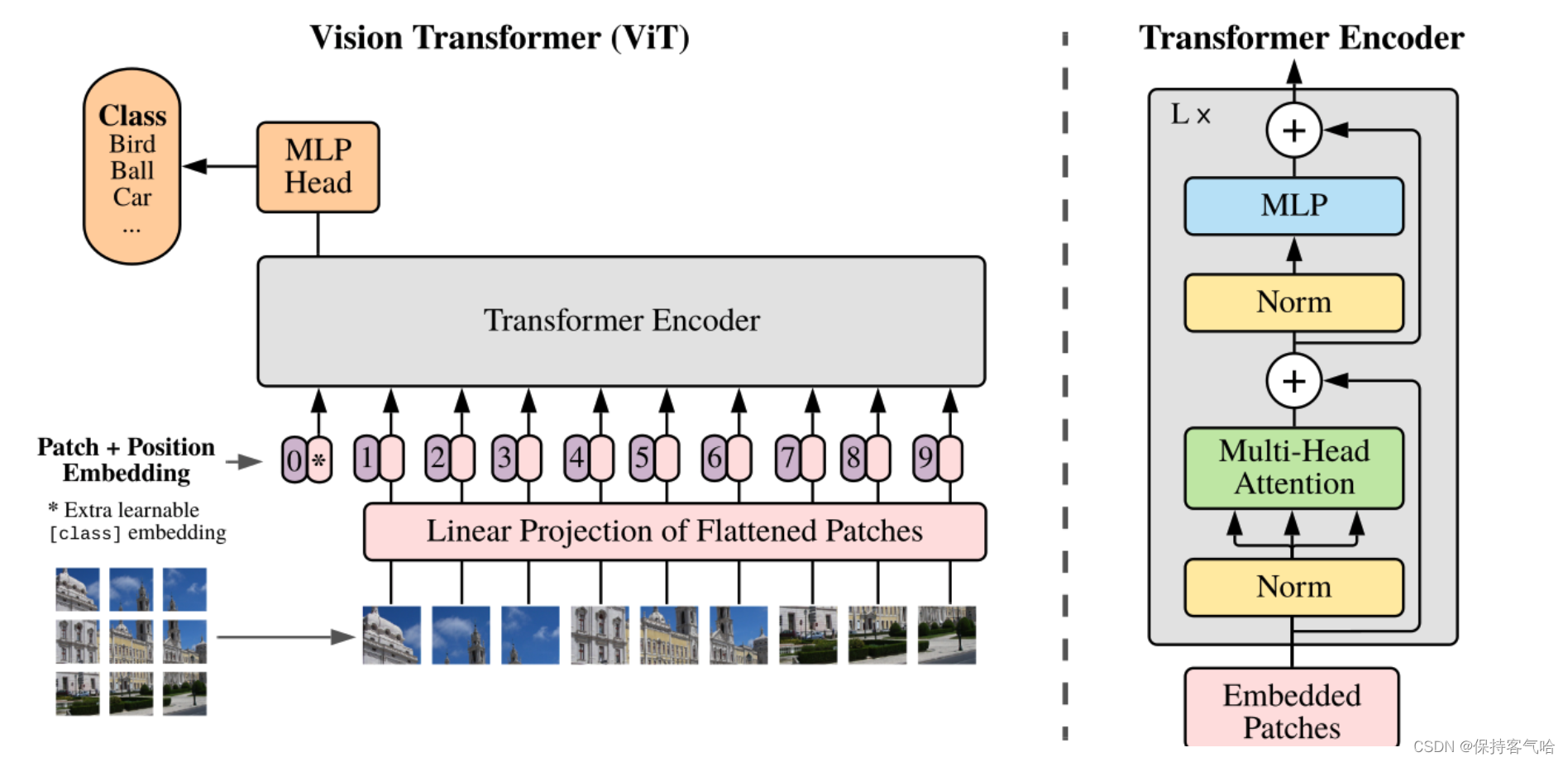
Embedding层结构详解

对于标准的Transformer模块，要求输入的是token（向量）序列，即二维矩阵[num_token, token_dim]，如下图所示，每个token对应的都是一个向量，以ViT-B/16为例，每个token向量长度为768。

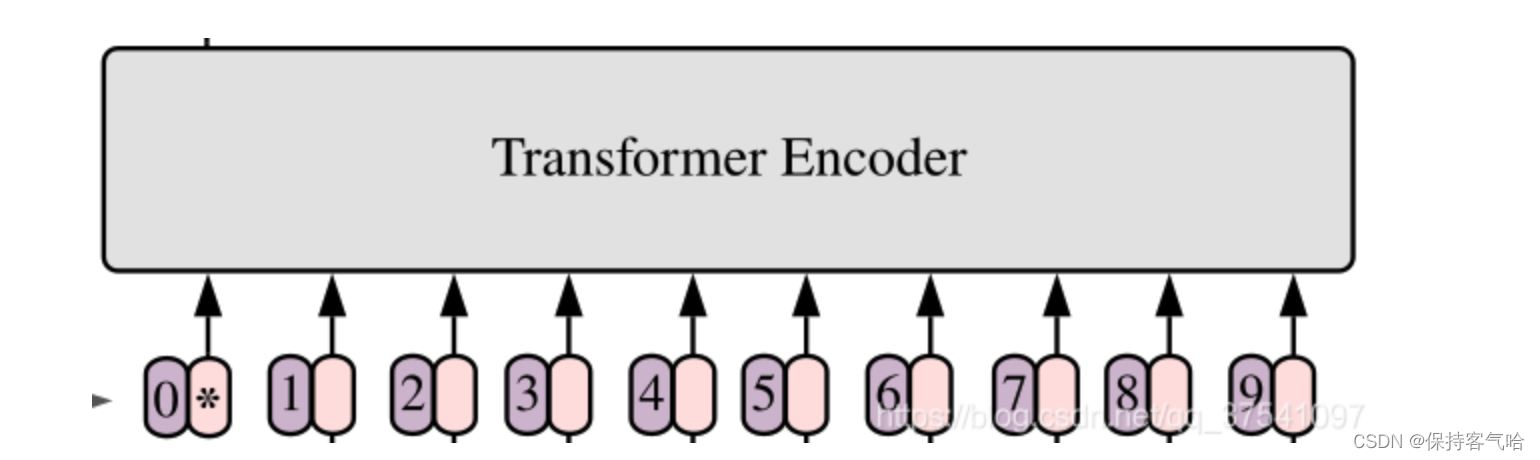
而对于图像数据而言，其数据格式为[H, W, C]是三维矩阵明显不是Transformer想要的。所以需要先通过一个Embedding层来对数据做个变换。如下图所示，首先将一张图片按给定大小分成一堆Patches。以ViT-B/16为例，将输入图片(224x224)按照16x16大小的Patch进行划分，划分后会得到$(224/16{)}^2=196$个Patches。接着通过线性映射将每个Patch映射到一维向量中，以ViT-B/16为例，每个Patch数据shape为[16, 16, 3]通过映射得到一个长度为768的向量（后面都直接称为token）。$[16,16,3]\to [768]$

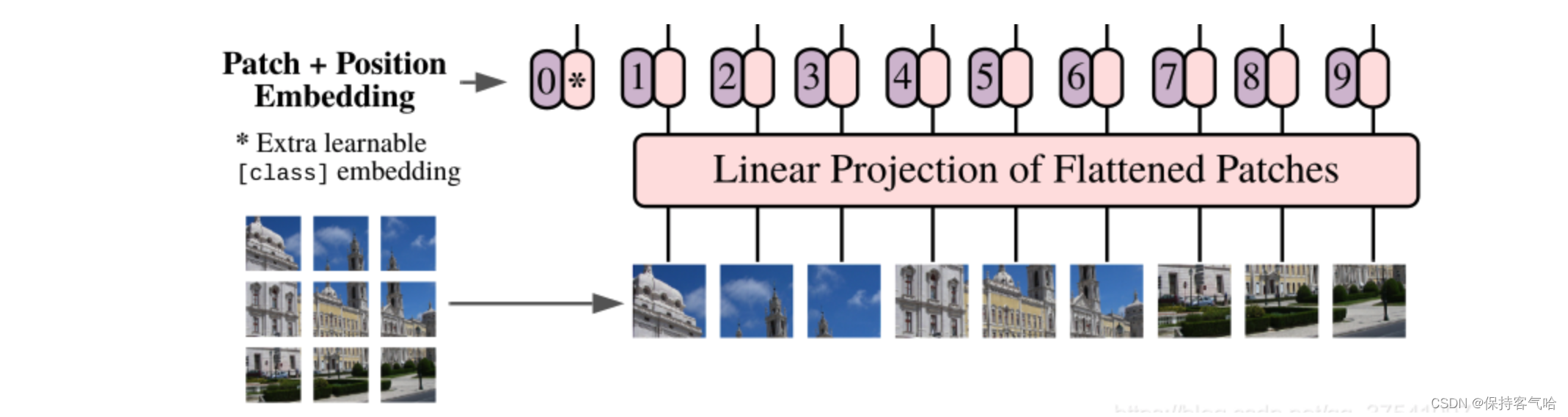
在代码实现中，直接通过一个卷积层来实现。以ViT-B/16为例，直接使用一个卷积核大小为16x16，步距为16，卷积核个数为768的卷积来实现。通过卷积$[224,224,3]\to [14,14,768]$，然后把H以及W两个维度展平即可$[14,14,768]\to [196,768]$，此时正好变成了一个二维矩阵，正是Transformer想要的。

在输入Transformer Encoder之前注意需要加上[class]token以及Position Embedding。 在原论文中，作者说参考BERT，在刚刚得到的一堆tokens中插入一个专门用于分类的[class]token，这个[class]token是一个可训练的参数，数据格式和其他token一样都是一个向量，以ViT-B/16为例，就是一个长度为768的向量，与之前从图片中生成的tokens拼接在一起，$Cat([1,768],[196,768])\to [197,768]$。然后关于Position Embedding就是之前Transformer中讲到的Positional Encoding，这里的Position Embedding采用的是一个可训练的参数（1D Pos. Emb.），是直接叠加在tokens上的（add），所以shape要一样。以ViT-B/16为例，刚刚拼接[class]token后shape是$[197,768]$，那么这里的Position Embedding的shape也是$[197,768]$。

对于Position Embedding作者也有做一系列对比试验，在源码中默认使用的是1D Pos. Emb.，对比不使用Position Embedding准确率提升了大概3个点，和2D Pos. Emb.比起来没太大差别。

Transformer Encoder详解

Transformer Encoder其实就是重复堆叠Encoder Block L次，下图是我自己绘制的Encoder Block，主要由以下几部分组成：

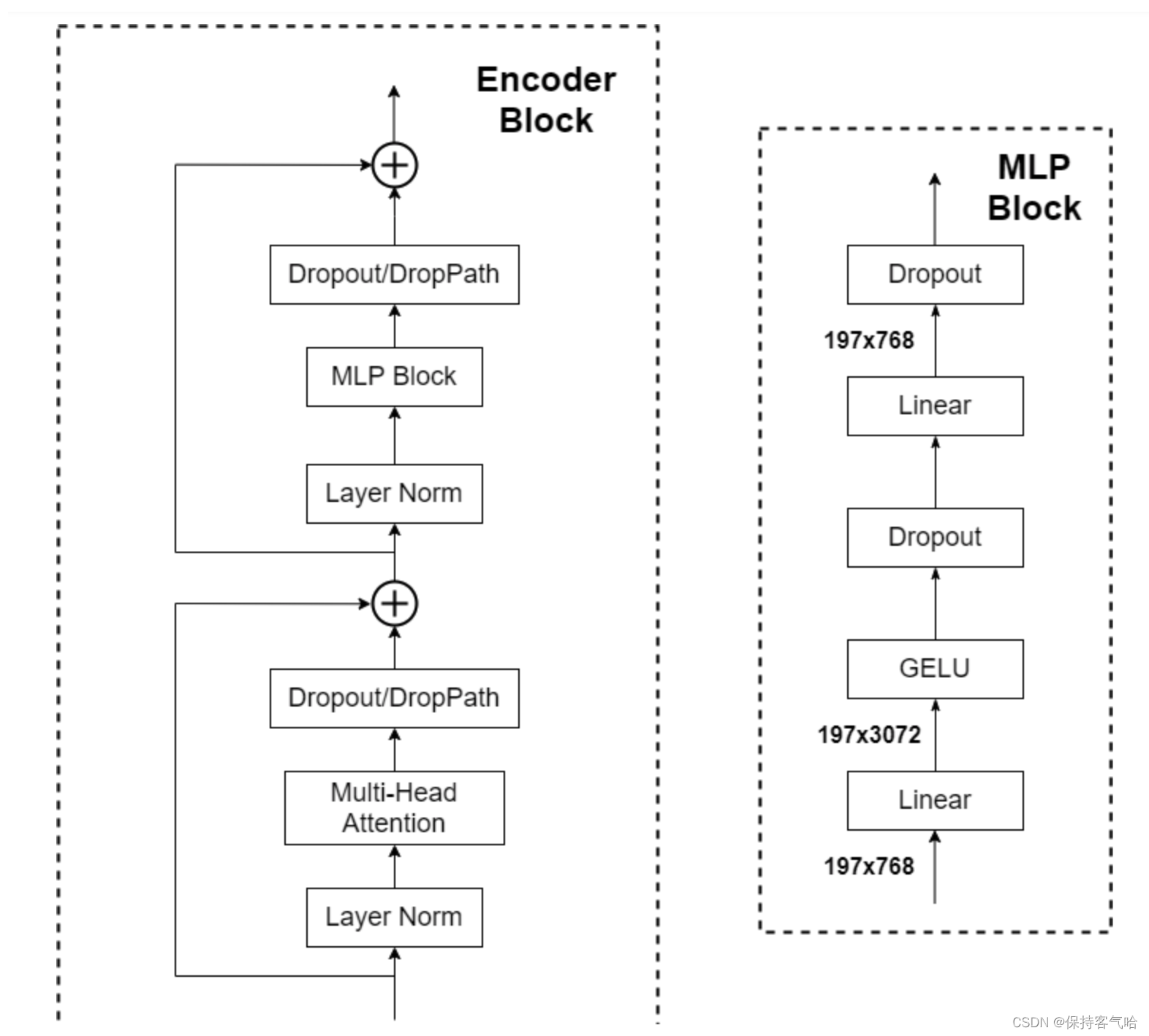
• Layer Norm，这种Normalization方法主要是针对NLP领域提出的，这里是对每个token进行Norm处理，之前也有讲过Layer Norm不懂的可以参考链接

• Multi-Head Attention，这个结构之前在讲Transformer中很详细的讲过，不在赘述，不了解的可以参考

• Dropout/DropPath，在原论文的代码中是直接使用的Dropout层，在但rwightman实现的代码中使用的是DropPath（stochastic depth），可能后者会更好一点。

• MLP Block，如图右侧所示，就是全连接+GELU激活函数+Dropout组成也非常简单，需要注意的是第一个全连接层会把输入节点个数翻4倍$[197,768]\to [197,3072]$，第二个全连接层会还原回原节点个数$[197,3072]\to [197,768]$。

MLP Head详解

在经过Transformer Encoder之后，输出的shape和输入的shape是保持不变的，以ViT-B/16为例，输入的是[197, 768]，输出的还是[197, 768]。注意，在Transformer Encoder后实际上还有一个Layer Norm层没有画出来，后面有我自己画的ViT的模型可以看到详细结构。

在分类任务中，我们只需要提取出[class]token对应的结果，即[197, 768]中抽取出[class]token对应的[1, 768]。接着通过MLP Head得到最终的分类结果。在原论文中，训练ImageNet21K时，MLP Head由Linear层、tanh激活函数、Linear层组成。但是在迁移到ImageNet1K上或者自己的数据集上时，只需要使用一个Linear层即可。

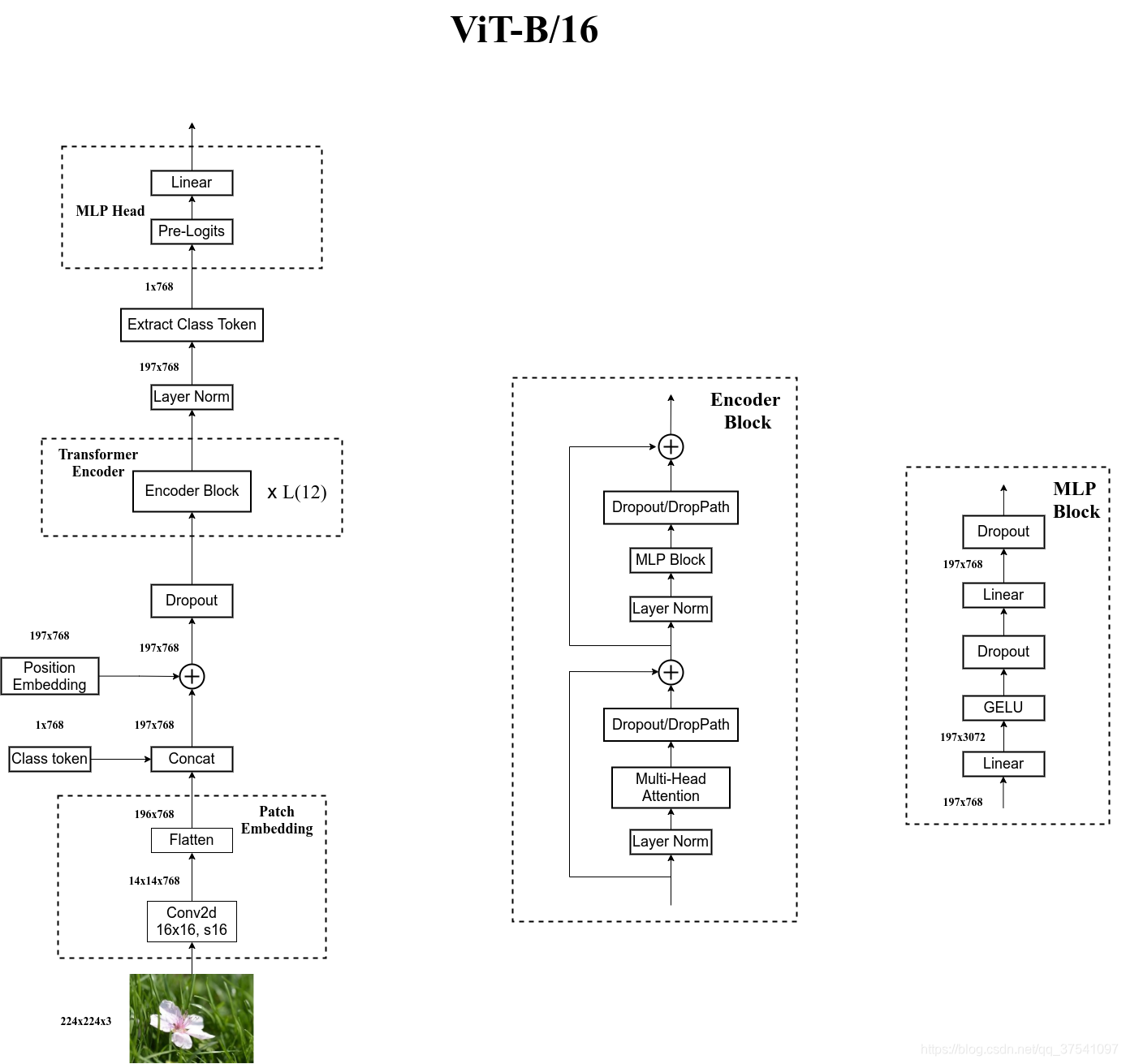
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-3CPz4RBi-1688792310268)(/Users/zhangkai/Library/Application Support/typora-user-images/image-20230708125431765.png)]

自己绘制的Vision Transformer网络结构

"""
original code from rwightman:
https://github.com/rwightman/pytorch-image-models/blob/master/timm/models/vision_transformer.py
"""
from functools import partial
from collections import OrderedDict

import torch
import torch.nn as nn


def drop_path(x, drop_prob: float = 0., training: bool = False):
    """
    Drop paths (Stochastic Depth) per sample (when applied in main path of residual blocks).
    This is the same as the DropConnect impl I created for EfficientNet, etc networks, however,
    the original name is misleading as 'Drop Connect' is a different form of dropout in a separate paper...
    See discussion: https://github.com/tensorflow/tpu/issues/494#issuecomment-532968956 ... I've opted for
    changing the layer and argument names to 'drop path' rather than mix DropConnect as a layer name and use
    'survival rate' as the argument.
    """
    if drop_prob == 0. or not training:
        return x
    keep_prob = 1 - drop_prob
    shape = (x.shape[0],) + (1,) * (x.ndim - 1)  # work with diff dim tensors, not just 2D ConvNets
    random_tensor = keep_prob + torch.rand(shape, dtype=x.dtype, device=x.device)
    random_tensor.floor_()  # binarize
    output = x.div(keep_prob) * random_tensor
    return output


class DropPath(nn.Module):
    """
    Drop paths (Stochastic Depth) per sample  (when applied in main path of residual blocks).
    """
    def __init__(self, drop_prob=None):
        super(DropPath, self).__init__()
        self.drop_prob = drop_prob

    def forward(self, x):
        return drop_path(x, self.drop_prob, self.training)


class PatchEmbed(nn.Module):
    """
    2D Image to Patch Embedding
    """
    def __init__(self, img_size=224, patch_size=16, in_c=3, embed_dim=768, norm_layer=None):
        super().__init__()
        img_size = (img_size, img_size)
        patch_size = (patch_size, patch_size)
        self.img_size = img_size
        self.patch_size = patch_size
        self.grid_size = (img_size[0] // patch_size[0], img_size[1] // patch_size[1])
        self.num_patches = self.grid_size[0] * self.grid_size[1]

        self.proj = nn.Conv2d(in_c, embed_dim, kernel_size=patch_size, stride=patch_size)
        self.norm = norm_layer(embed_dim) if norm_layer else nn.Identity()

    def forward(self, x):
        B, C, H, W = x.shape
        assert H == self.img_size[0] and W == self.img_size[1], \
            f"Input image size ({H}*{W}) doesn't match model ({self.img_size[0]}*{self.img_size[1]})."

        # flatten: [B, C, H, W] -> [B, C, HW]
        # transpose: [B, C, HW] -> [B, HW, C]
        x = self.proj(x).flatten(2).transpose(1, 2)
        x = self.norm(x)
        return x


class Attention(nn.Module):
    def __init__(self,
                 dim,   # 输入token的dim
                 num_heads=8,
                 qkv_bias=False,
                 qk_scale=None,
                 attn_drop_ratio=0.,
                 proj_drop_ratio=0.):
        super(Attention, self).__init__()
        self.num_heads = num_heads
        head_dim = dim // num_heads
        self.scale = qk_scale or head_dim ** -0.5
        self.qkv = nn.Linear(dim, dim * 3, bias=qkv_bias)
        self.attn_drop = nn.Dropout(attn_drop_ratio)
        self.proj = nn.Linear(dim, dim)
        self.proj_drop = nn.Dropout(proj_drop_ratio)

    def forward(self, x):
        # [batch_size, num_patches + 1, total_embed_dim]
        B, N, C = x.shape

        # qkv(): -> [batch_size, num_patches + 1, 3 * total_embed_dim]
        # reshape: -> [batch_size, num_patches + 1, 3, num_heads, embed_dim_per_head]
        # permute: -> [3, batch_size, num_heads, num_patches + 1, embed_dim_per_head]
        qkv = self.qkv(x).reshape(B, N, 3, self.num_heads, C // self.num_heads).permute(2, 0, 3, 1, 4)
        # [batch_size, num_heads, num_patches + 1, embed_dim_per_head]
        q, k, v = qkv[0], qkv[1], qkv[2]  # make torchscript happy (cannot use tensor as tuple)

        # transpose: -> [batch_size, num_heads, embed_dim_per_head, num_patches + 1]
        # @: multiply -> [batch_size, num_heads, num_patches + 1, num_patches + 1]
        attn = (q @ k.transpose(-2, -1)) * self.scale
        attn = attn.softmax(dim=-1)
        attn = self.attn_drop(attn)

        # @: multiply -> [batch_size, num_heads, num_patches + 1, embed_dim_per_head]
        # transpose: -> [batch_size, num_patches + 1, num_heads, embed_dim_per_head]
        # reshape: -> [batch_size, num_patches + 1, total_embed_dim]
        x = (attn @ v).transpose(1, 2).reshape(B, N, C)
        x = self.proj(x)
        x = self.proj_drop(x)
        return x


class Mlp(nn.Module):
    """
    MLP as used in Vision Transformer, MLP-Mixer and related networks
    """
    def __init__(self, in_features, hidden_features=None, out_features=None, act_layer=nn.GELU, drop=0.):
        super().__init__()
        out_features = out_features or in_features
        hidden_features = hidden_features or in_features
        self.fc1 = nn.Linear(in_features, hidden_features)
        self.act = act_layer()
        self.fc2 = nn.Linear(hidden_features, out_features)
        self.drop = nn.Dropout(drop)

    def forward(self, x):
        x = self.fc1(x)
        x = self.act(x)
        x = self.drop(x)
        x = self.fc2(x)
        x = self.drop(x)
        return x


class Block(nn.Module):
    def __init__(self,
                 dim,
                 num_heads,
                 mlp_ratio=4.,
                 qkv_bias=False,
                 qk_scale=None,
                 drop_ratio=0.,
                 attn_drop_ratio=0.,
                 drop_path_ratio=0.,
                 act_layer=nn.GELU,
                 norm_layer=nn.LayerNorm):
        super(Block, self).__init__()
        self.norm1 = norm_layer(dim)
        self.attn = Attention(dim, num_heads=num_heads, qkv_bias=qkv_bias, qk_scale=qk_scale,
                              attn_drop_ratio=attn_drop_ratio, proj_drop_ratio=drop_ratio)
        # NOTE: drop path for stochastic depth, we shall see if this is better than dropout here
        self.drop_path = DropPath(drop_path_ratio) if drop_path_ratio > 0. else nn.Identity()
        self.norm2 = norm_layer(dim)
        mlp_hidden_dim = int(dim * mlp_ratio)
        self.mlp = Mlp(in_features=dim, hidden_features=mlp_hidden_dim, act_layer=act_layer, drop=drop_ratio)

    def forward(self, x):
        x = x + self.drop_path(self.attn(self.norm1(x)))
        x = x + self.drop_path(self.mlp(self.norm2(x)))
        return x


class VisionTransformer(nn.Module):
    def __init__(self, img_size=224, patch_size=16, in_c=3, num_classes=1000,
                 embed_dim=768, depth=12, num_heads=12, mlp_ratio=4.0, qkv_bias=True,
                 qk_scale=None, representation_size=None, distilled=False, drop_ratio=0.,
                 attn_drop_ratio=0., drop_path_ratio=0., embed_layer=PatchEmbed, norm_layer=None,
                 act_layer=None):
        """
        Args:
            img_size (int, tuple): input image size
            patch_size (int, tuple): patch size
            in_c (int): number of input channels
            num_classes (int): number of classes for classification head
            embed_dim (int): embedding dimension
            depth (int): depth of transformer
            num_heads (int): number of attention heads
            mlp_ratio (int): ratio of mlp hidden dim to embedding dim
            qkv_bias (bool): enable bias for qkv if True
            qk_scale (float): override default qk scale of head_dim ** -0.5 if set
            representation_size (Optional[int]): enable and set representation layer (pre-logits) to this value if set
            distilled (bool): model includes a distillation token and head as in DeiT models
            drop_ratio (float): dropout rate
            attn_drop_ratio (float): attention dropout rate
            drop_path_ratio (float): stochastic depth rate
            embed_layer (nn.Module): patch embedding layer
            norm_layer: (nn.Module): normalization layer
        """
        super(VisionTransformer, self).__init__()
        self.num_classes = num_classes
        self.num_features = self.embed_dim = embed_dim  # num_features for consistency with other models
        self.num_tokens = 2 if distilled else 1
        norm_layer = norm_layer or partial(nn.LayerNorm, eps=1e-6)
        act_layer = act_layer or nn.GELU

        self.patch_embed = embed_layer(img_size=img_size, patch_size=patch_size, in_c=in_c, embed_dim=embed_dim)
        num_patches = self.patch_embed.num_patches

        self.cls_token = nn.Parameter(torch.zeros(1, 1, embed_dim))
        self.dist_token = nn.Parameter(torch.zeros(1, 1, embed_dim)) if distilled else None
        self.pos_embed = nn.Parameter(torch.zeros(1, num_patches + self.num_tokens, embed_dim))
        self.pos_drop = nn.Dropout(p=drop_ratio)

        dpr = [x.item() for x in torch.linspace(0, drop_path_ratio, depth)]  # stochastic depth decay rule
        self.blocks = nn.Sequential(*[
            Block(dim=embed_dim, num_heads=num_heads, mlp_ratio=mlp_ratio, qkv_bias=qkv_bias, qk_scale=qk_scale,
                  drop_ratio=drop_ratio, attn_drop_ratio=attn_drop_ratio, drop_path_ratio=dpr[i],
                  norm_layer=norm_layer, act_layer=act_layer)
            for i in range(depth)
        ])
        self.norm = norm_layer(embed_dim)

        # Representation layer
        if representation_size and not distilled:
            self.has_logits = True
            self.num_features = representation_size
            self.pre_logits = nn.Sequential(OrderedDict([
                ("fc", nn.Linear(embed_dim, representation_size)),
                ("act", nn.Tanh())
            ]))
        else:
            self.has_logits = False
            self.pre_logits = nn.Identity()

        # Classifier head(s)
        self.head = nn.Linear(self.num_features, num_classes) if num_classes > 0 else nn.Identity()
        self.head_dist = None
        if distilled:
            self.head_dist = nn.Linear(self.embed_dim, self.num_classes) if num_classes > 0 else nn.Identity()

        # Weight init
        nn.init.trunc_normal_(self.pos_embed, std=0.02)
        if self.dist_token is not None:
            nn.init.trunc_normal_(self.dist_token, std=0.02)

        nn.init.trunc_normal_(self.cls_token, std=0.02)
        self.apply(_init_vit_weights)

    def forward_features(self, x):
        # [B, C, H, W] -> [B, num_patches, embed_dim]
        x = self.patch_embed(x)  # [B, 196, 768]
        # [1, 1, 768] -> [B, 1, 768]
        cls_token = self.cls_token.expand(x.shape[0], -1, -1)
        if self.dist_token is None:
            x = torch.cat((cls_token, x), dim=1)  # [B, 197, 768]
        else:
            x = torch.cat((cls_token, self.dist_token.expand(x.shape[0], -1, -1), x), dim=1)

        x = self.pos_drop(x + self.pos_embed)
        x = self.blocks(x)
        x = self.norm(x)
        if self.dist_token is None:
            return self.pre_logits(x[:, 0])
        else:
            return x[:, 0], x[:, 1]

    def forward(self, x):
        x = self.forward_features(x)
        if self.head_dist is not None:
            x, x_dist = self.head(x[0]), self.head_dist(x[1])
            if self.training and not torch.jit.is_scripting():
                # during inference, return the average of both classifier predictions
                return x, x_dist
            else:
                return (x + x_dist) / 2
        else:
            x = self.head(x)
        return x


def _init_vit_weights(m):
    """
    ViT weight initialization
    :param m: module
    """
    if isinstance(m, nn.Linear):
        nn.init.trunc_normal_(m.weight, std=.01)
        if m.bias is not None:
            nn.init.zeros_(m.bias)
    elif isinstance(m, nn.Conv2d):
        nn.init.kaiming_normal_(m.weight, mode="fan_out")
        if m.bias is not None:
            nn.init.zeros_(m.bias)
    elif isinstance(m, nn.LayerNorm):
        nn.init.zeros_(m.bias)
        nn.init.ones_(m.weight)


def vit_base_patch16_224(num_classes: int = 1000):
    """
    ViT-Base model (ViT-B/16) from original paper (https://arxiv.org/abs/2010.11929).
    ImageNet-1k weights @ 224x224, source https://github.com/google-research/vision_transformer.
    weights ported from official Google JAX impl:
    链接: https://pan.baidu.com/s/1zqb08naP0RPqqfSXfkB2EA  密码: eu9f
    """
    model = VisionTransformer(img_size=224,
                              patch_size=16,
                              embed_dim=768,
                              depth=12,
                              num_heads=12,
                              representation_size=None,
                              num_classes=num_classes)
    return model


def vit_base_patch16_224_in21k(num_classes: int = 21843, has_logits: bool = True):
    """
    ViT-Base model (ViT-B/16) from original paper (https://arxiv.org/abs/2010.11929).
    ImageNet-21k weights @ 224x224, source https://github.com/google-research/vision_transformer.
    weights ported from official Google JAX impl:
    https://github.com/rwightman/pytorch-image-models/releases/download/v0.1-vitjx/jx_vit_base_patch16_224_in21k-e5005f0a.pth
    """
    model = VisionTransformer(img_size=224,
                              patch_size=16,
                              embed_dim=768,
                              depth=12,
                              num_heads=12,
                              representation_size=768 if has_logits else None,
                              num_classes=num_classes)
    return model


def vit_base_patch32_224(num_classes: int = 1000):
    """
    ViT-Base model (ViT-B/32) from original paper (https://arxiv.org/abs/2010.11929).
    ImageNet-1k weights @ 224x224, source https://github.com/google-research/vision_transformer.
    weights ported from official Google JAX impl:
    链接: https://pan.baidu.com/s/1hCv0U8pQomwAtHBYc4hmZg  密码: s5hl
    """
    model = VisionTransformer(img_size=224,
                              patch_size=32,
                              embed_dim=768,
                              depth=12,
                              num_heads=12,
                              representation_size=None,
                              num_classes=num_classes)
    return model


def vit_base_patch32_224_in21k(num_classes: int = 21843, has_logits: bool = True):
    """
    ViT-Base model (ViT-B/32) from original paper (https://arxiv.org/abs/2010.11929).
    ImageNet-21k weights @ 224x224, source https://github.com/google-research/vision_transformer.
    weights ported from official Google JAX impl:
    https://github.com/rwightman/pytorch-image-models/releases/download/v0.1-vitjx/jx_vit_base_patch32_224_in21k-8db57226.pth
    """
    model = VisionTransformer(img_size=224,
                              patch_size=32,
                              embed_dim=768,
                              depth=12,
                              num_heads=12,
                              representation_size=768 if has_logits else None,
                              num_classes=num_classes)
    return model


def vit_large_patch16_224(num_classes: int = 1000):
    """
    ViT-Large model (ViT-L/16) from original paper (https://arxiv.org/abs/2010.11929).
    ImageNet-1k weights @ 224x224, source https://github.com/google-research/vision_transformer.
    weights ported from official Google JAX impl:
    链接: https://pan.baidu.com/s/1cxBgZJJ6qUWPSBNcE4TdRQ  密码: qqt8
    """
    model = VisionTransformer(img_size=224,
                              patch_size=16,
                              embed_dim=1024,
                              depth=24,
                              num_heads=16,
                              representation_size=None,
                              num_classes=num_classes)
    return model


def vit_large_patch16_224_in21k(num_classes: int = 21843, has_logits: bool = True):
    """
    ViT-Large model (ViT-L/16) from original paper (https://arxiv.org/abs/2010.11929).
    ImageNet-21k weights @ 224x224, source https://github.com/google-research/vision_transformer.
    weights ported from official Google JAX impl:
    https://github.com/rwightman/pytorch-image-models/releases/download/v0.1-vitjx/jx_vit_large_patch16_224_in21k-606da67d.pth
    """
    model = VisionTransformer(img_size=224,
                              patch_size=16,
                              embed_dim=1024,
                              depth=24,
                              num_heads=16,
                              representation_size=1024 if has_logits else None,
                              num_classes=num_classes)
    return model


def vit_large_patch32_224_in21k(num_classes: int = 21843, has_logits: bool = True):
    """
    ViT-Large model (ViT-L/32) from original paper (https://arxiv.org/abs/2010.11929).
    ImageNet-21k weights @ 224x224, source https://github.com/google-research/vision_transformer.
    weights ported from official Google JAX impl:
    https://github.com/rwightman/pytorch-image-models/releases/download/v0.1-vitjx/jx_vit_large_patch32_224_in21k-9046d2e7.pth
    """
    model = VisionTransformer(img_size=224,
                              patch_size=32,
                              embed_dim=1024,
                              depth=24,
                              num_heads=16,
                              representation_size=1024 if has_logits else None,
                              num_classes=num_classes)
    return model


def vit_huge_patch14_224_in21k(num_classes: int = 21843, has_logits: bool = True):
    """
    ViT-Huge model (ViT-H/14) from original paper (https://arxiv.org/abs/2010.11929).
    ImageNet-21k weights @ 224x224, source https://github.com/google-research/vision_transformer.
    NOTE: converted weights not currently available, too large for github release hosting.
    """
    model = VisionTransformer(img_size=224,
                              patch_size=14,
                              embed_dim=1280,
                              depth=32,
                              num_heads=16,
                              representation_size=1280 if has_logits else None,
                              num_classes=num_classes)
    return model

Reference：太阳花的小绿豆