文章目录

第五章神经网络
- 5.1神经元模型
- 5.2感知机与多层网络
- 5.3误差逆传播算法
- 5.4全局最小和局部最小
- 5.5其他常见神经网络
- - 5.5.1RBF网络
  - 5.5.2ART网络
  - 5.5.3SOM网络
  - 5.5.4级联相关网络
  - 5.5.5Elman网络
  - 5.5.6Boltzmann机
- 5.6深度学习
- 5.7实验：手写数字识别

第五章神经网络

5.1神经元模型

神经网络中最基本的成分是神经元。每个神经元与其他神经元相连,当它“兴奋”时,就会向相连的神经元发送化学物质，从而改变这些神经元内的电位;如果某神经元的电位超过了一个“阈值”(threshold)，那么它就会被激活,即“兴奋”起来,向其他神经元发送化学物质.
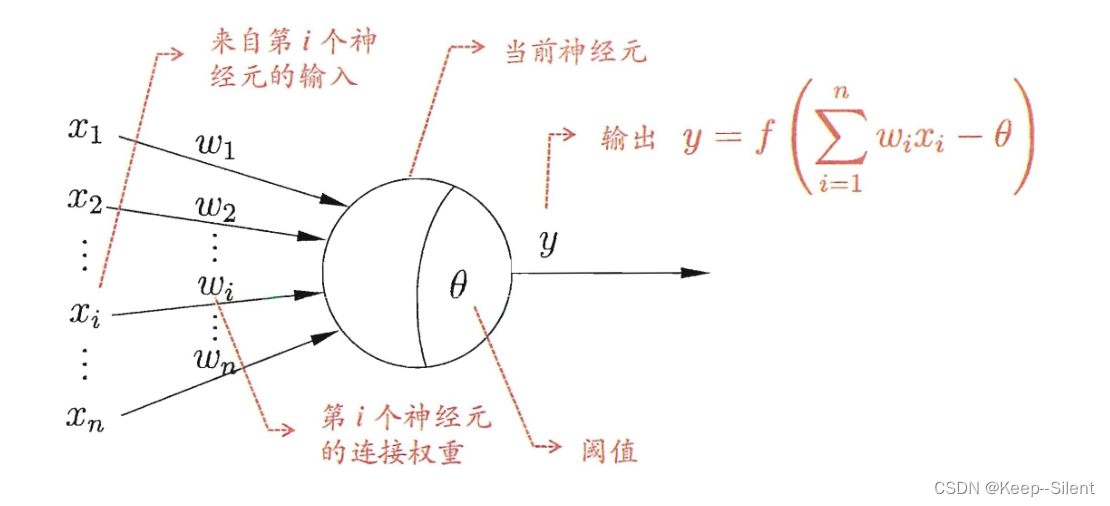
在这里插入图片描述
MP神经元模型：神经元接收到来自n个其他神经元传递过来的输入信号,这些输入信号通过带权重的连接进行传递,神经元接收到的总输入值将与神经元的阈值进行比，然后通过激活函数处理以产生神经元的输出。
两个常见的激活函数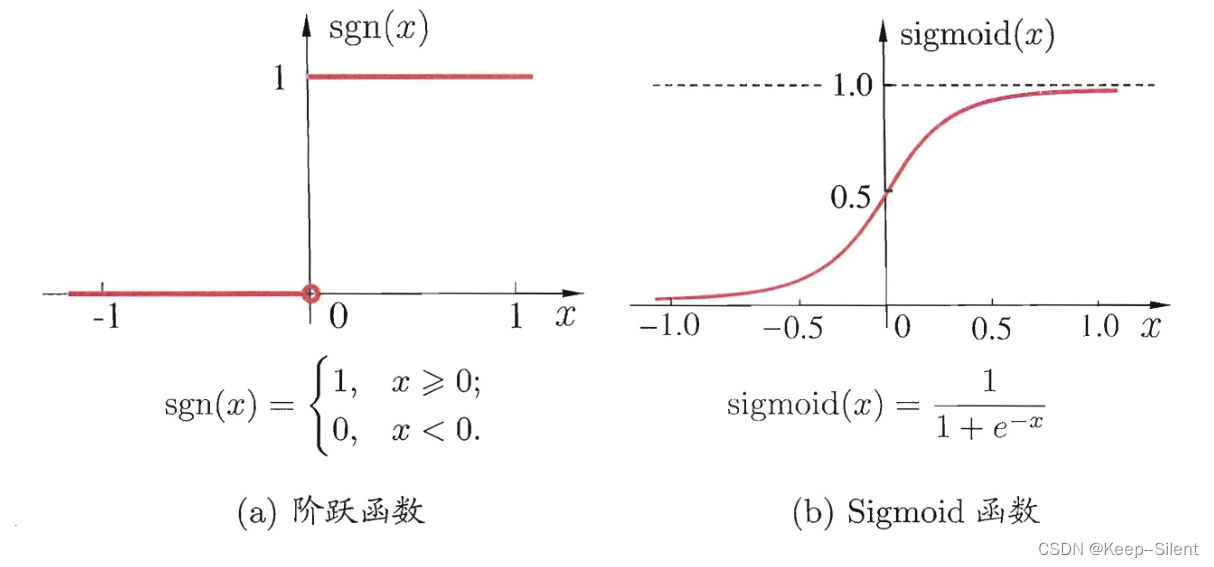：在这里插入图片描述

5.2感知机与多层网络

感知机(Perceptron)由两层神经元组成，输入层接收外界输入信号后传递给输出层，输出层是 M-P神经元,亦称“阈值逻辑单元”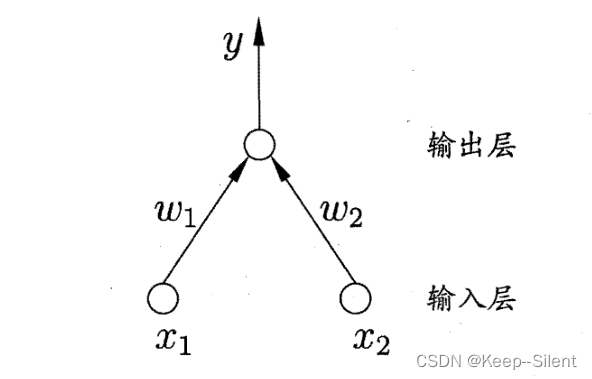：在这里插入图片描述
感知机容易实现逻辑与、或、非：

与（ $x_1 \land x_2$ ）： $y=f(1*x_1+1*x_2-2)$ ，仅当 $x_1=x_2=1$ ， $y = 1$
或（ $x_{1}\vee x_{2}$ ）： $y=f(1*x_1+1*x_2-0.5)$ ，当 $x_1=1$ 或 $x_2=1$ ， $y = 1$
非（ $\neg x_1$ ）： $y=f(-0.6*x_1+0.5)$ ，当 $x_1=0$ ， $y = 1$ ；当 $x_1=1$ ， $y = 0$

如果存在一个线性超平面两类模式分开，则感知机可收敛；否则振荡，如下图的异或
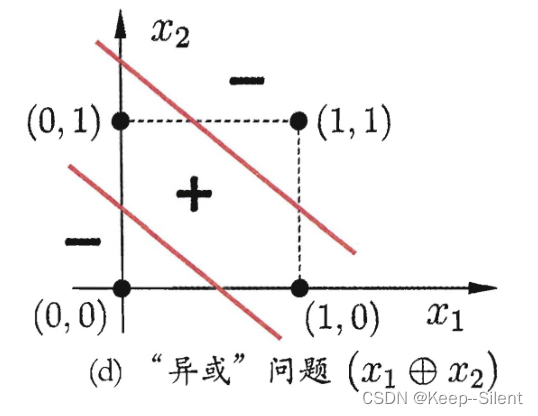
在这里插入图片描述
要解决非线性可分问题，需要多层功能神经元。
两层感知机：输入层和输出层加一层隐含层

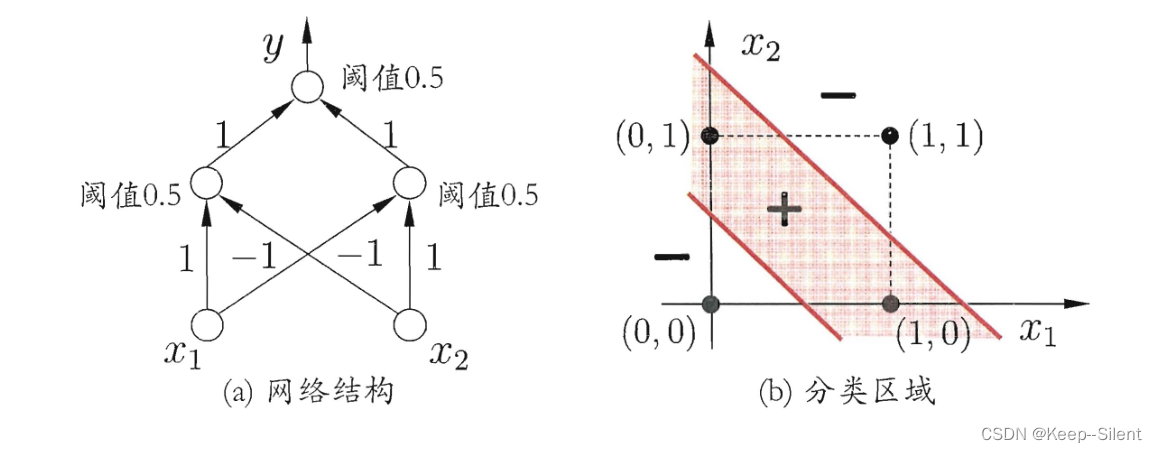
多层前馈神经网络：每一层神经元全互连,神经元之间不存在同层连接,也不存在跨层连接

5.3误差逆传播算法

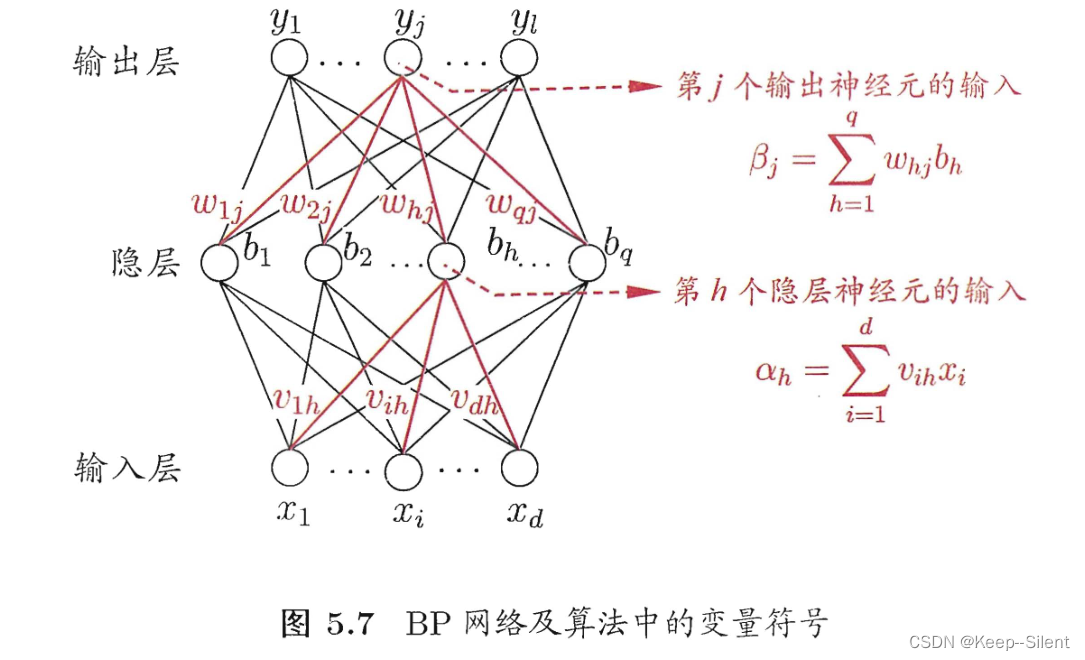
误差逆传播算法（BP算法）是迄今最成功的神经学习网络（通常说BP网络时指的是多层前馈神经网络）。
在这里插入图片描述
训练集： $D=\{(\boldsymbol{x}_1,\boldsymbol{y}_1),(\boldsymbol{x}_2,\boldsymbol{y}_2),\ldots,(\boldsymbol{x}_m,\boldsymbol{y}_m)\},\boldsymbol{x}_i\in\mathbb{R}^d,\boldsymbol{y}_i\in\mathbb{R}^l,$
输入 $d$ 个属性，输出 $l$ 维向量。
则采用输入层 $d$ 个神经元 $x$ 、 $q$ 个隐层神经元 $b$ 、输出层 $l$ 个神经元 $y$ 的多层前馈神经网络（BP网络）。
临时变量：输入层为第 $i$ 个神经元、隐层为第 $h$ 个神经元、输出层为第 $j$ 层神经元
连接权：输入层第i个神经元与隐层第h个神经元的连接权为 $v_{ih}$ 、隐层第 $h$ 个神经元与输出层第 $j$ 个神经元的连接权为 $w_{hj}$
阈值：隐层第 $h$ 个神经元的阈值： $\gamma_{h}$ 、输出层第 $j$ 个神经元的阈值： $\theta _j$

输入：第 $h$ 个神经元的输入为 $\alpha_h=\sum_{i=1}^dv_{ih}x_i$ ，输出层第 $j$ 个神经元的为 $\beta_{j}=\sum_{h=1}^{q}w_{hj}b_{h}$

假设激活函数使用Sigmoid函数。假定神经网络的输出为 $y_{k}=(\hat{y}_{1}^{k}, \hat{y}_{2}^{k},\ldots,\hat{y}_{l}^{k})$ ，即 $\hat{y}_j^k=f (\beta_j-\theta_j)$ 网络均方误差为 $E_k=\frac12\sum_{j=1}^l(\hat{y}_j^k-y_j^k)^2$

需要确定的参数：

输入层到隐层dq个权值
隐层到输出层ql个权值
q个隐层神经元的阈值
l个输出层神经元的阈值

$\begin{aligned} g_j& =-\frac{\partial E_{k}}{\partial\hat{y}_{j}^{k}}\cdot\frac{\partial\hat{y}_{j}^{k}}{\partial\beta_{j}} \\ &=-(\hat{y}_{j}^{k}-y_{j}^{k})f^{\prime}(\beta_{j}-\theta_{j}) \\ &=\hat{y}_j^k(1-\hat{y}_j^k)(y_j^k-\hat{y}_j^k). \end{aligned}$

$\begin{gathered} \Delta w_{hj} =\eta g_{j}b_{h} \\ \Delta\theta_{j} =-\eta g_{j} \\ \Delta v_{ih} =\eta e_hx_i \\ \Delta\gamma_{h} =-\eta e_{h} \end{gathered}$

$\begin{aligned} e_{h}& =-\frac{\partial E_k}{\partial b_h}\cdot\frac{\partial b_h}{\partial\alpha_h} \\ &=-\sum_{j=1}^{l}\frac{\partial E_{k}}{\partial\beta_{j}}\cdot\frac{\partial\beta_{j}}{\partial b_{h}}f^{\prime}(\alpha_{h}-\gamma_{h}) \\ &=\sum_{j=1}^lw_{hj}g_jf^{\prime}(\alpha_h-\gamma_h) \\ &=b_h(1-b_h)\sum_{j=1}^lw_{hj}g_j \end{aligned}$

误差逆传播算法
输入：训练集 $D=\{(\boldsymbol{x}_1,\boldsymbol{y}_1),(\boldsymbol{x}_2,\boldsymbol{y}_2),\ldots,(\boldsymbol{x}_m,\boldsymbol{y}_m)\}$ ，学习率 $\eta$
过程：

在(0,1)范围内随机初始化网络中所有连接权和阈值
repeat：
    for (xk, yk) in D :
        计算当前样本的输出y'k
        计算输出层神经元的梯度项g_j
        计算隐层神经元的梯度项e_h
        更新连接权w_hj，v_ih与阈值theta_j，gamma_h
    end for
until 达到停止条件

输出：连接权与阈值确定的多层前馈神经网络

5.4全局最小和局部最小

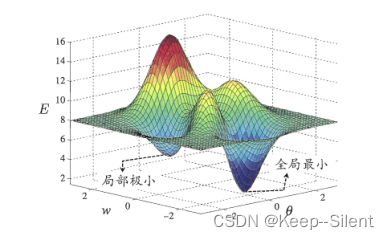
在这里插入图片描述

基于梯度的搜索中,我们从某些初始解出发,迭代寻找最优参数值.每次迭代中,我们先计算误差函数在当前点的梯度,然后根据梯度确定搜索方向.例如，由于负梯度方向是函数值下降最快的方向,因此梯度下降法就是沿着负梯度方向搜索最优解．若误差函数在当前点的梯度为零,则已达到局部极小，更新量将为零,这意味着参数的迭代更新将在此停止.然而，如果误差函数具有多个局部极小，则不能保证找到的解是全局最小.

在现实任务中，人们常采用以下策略来试图“跳出”局部极小，从而进一步接近全局最小:

以多组不同参数值初始化多个神经网络,按标准方法训练后,取其中误差最小的解作为最终参数.这相当于从多个不同的初始点开始搜索,这样就可能陷入不同的局部极小，从中进行选择有可能获得更接近全局最小的结果.
使用“模拟退火”(simulated annealing)技术.模拟退火在每一步都以一定的概率接受比当前解更差的结果,从而有助于“跳出”局部极小.在每步迭代过程中,接受“次优解”的概率要随着时间的推移而逐渐降低,从而保证算法稳定.
使用随机梯度下降.与标准梯度下降法精确计算梯度不同,随机梯度下降法在计算梯度时加入了随机因素.于是,即便陷入局部极小点,它计算出的梯度仍可能不为零,这样就有机会跳出局部极小继续搜索.

上述用于跳出局部极小的技术大多是启发式,理论上.尚缺乏保障.

5.5其他常见神经网络

5.5.1RBF网络

RBF（径向基函数）网络是一种常用于模式识别和函数逼近任务的人工神经网络。RBF网络由三层组成：输入层、具有径向基函数神经元的隐藏层和输出层：

输入层：输入层接收输入数据，这些数据可以是数值或分类变量。输入层的每个神经元代表输入数据的一个特征或属性。
隐藏层：隐藏层包含径向基函数神经元。该层的每个神经元使用径向基函数计算其输入与输入空间中的中心点之间的相似性。径向基函数通常是高斯函数。每个隐藏神经元的输出表示该神经元基于输入数据的激活水平。
输出层：输出层将隐藏层的激活组合起来产生网络的最终输出。

RPF网络可表示为 $\varphi(\boldsymbol{x})= \sum_{i=1}^{q}w_{i}\rho( \boldsymbol{x},\boldsymbol{c}_{i})$ 常用高斯径向基函数： $\rho(\boldsymbol{x} ,\boldsymbol{c}_{i}) = e^{-\beta_{i}\| \boldsymbol{x}-\boldsymbol{c}_{i} \|^{2}}$

5.5.2ART网络

ART（自适应共振理论）网络是一种人工神经网络，旨在模拟大脑处理和组织信息的方式。ART网络在涉及模式识别、分类和聚类等任务中非常有用。
ART网络的简要工作原理：

输入层：输入层接收输入数据，这些数据可以是数值或分类变量。每个输入神经元表示输入数据的一个特征或属性。
识别层：识别层包含神经元，这些神经元将输入模式与网络内存中存储的模式进行比较。这些神经元使用匹配规则（如余弦相似度或欧几里得距离）计算输入模式与存储模式之间的相似性。具有最高相似性的神经元成为获胜神经元。
警觉参数：警觉参数控制网络对新模式的敏感性。它确定输入模式与存储模式的相似度必须达到何种程度，识别神经元才会激活。较高的警觉值意味着网络对接受新模式更加严格。
重置和学习：如果输入模式与获胜神经元的存储模式的相似度低于警觉阈值，网络将将输入模式视为新类别，并激活一个新的神经元。这个过程称为重置。网络会根据新模式调整其内部权重，以适应新的输入模式。

5.5.3SOM网络

SOM（Self-Organizing Map，自组织映射）网络是一种常用的无监督学习算法，用于聚类、可视化和特征提取等任务。它是一种基于神经网络的数据降维和模式识别方法。
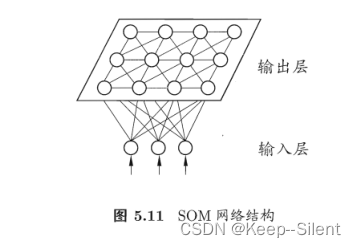
在这里插入图片描述
SOM网络的基本原理：

网络结构：SOM网络由一个二维的神经元网格组成，每个神经元代表一个特征向量的权重向量。
自组织过程：SOM网络通过自组织过程将输入数据映射到神经元网格上。在初始化阶段，每个神经元的权重向量被随机初始化。然后，根据输入数据的相似度，选择与输入数据最匹配的神经元作为获胜神经元。
邻域函数：获胜神经元及其周围神经元的权重向量会受到调整，使它们更接近输入数据。这种调整是通过邻域函数实现的，邻域函数定义了获胜神经元周围神经元的影响程度。
迭代更新：通过反复迭代更新过程，SOM网络逐渐调整神经元的权重向量，使其能够更好地反映输入数据的统计特性。迭代的过程中，邻域函数逐渐减小，使得调整范围逐渐缩小，最终形成一个聚类结果或者数据的拓扑映射。

SOM网络能够有效地对高维数据进行降维和聚类，同时保留了输入数据的拓扑结构。它在可视化数据、模式识别、图像处理等领域具有广泛应用。

5.5.4级联相关网络

级联相关网络（Cascade Correlation Network）是一种神经网络结构，它具有自适应的网络拓扑和动态构建连接的能力。级联相关网络用于解决神经网络训练中的困难问题。
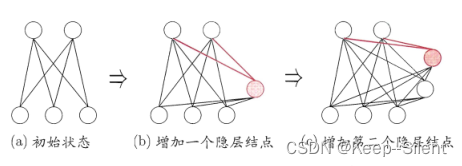
在这里插入图片描述
级联相关网络的基本原理：

动态网络拓扑：级联相关网络具有动态构建网络拓扑的能力。它开始时只有一个输入层和一个输出层，没有任何隐藏层。隐藏层是通过逐步添加神经元来动态构建的。
逐步添加神经元：训练过程中，级联相关网络逐步添加隐藏层神经元。每次添加一个神经元，它与前面层的神经元建立连接，并通过局部训练算法进行训练。新添加的神经元被训练来最大化网络性能的提升。
反向传播和监督训练：级联相关网络使用反向传播算法进行监督训练。在每个训练阶段，新添加的神经元以及前面层的所有神经元都参与误差反向传播的计算和权重调整。
增量训练：级联相关网络采用增量训练策略，每次只训练一个新添加的神经元。这种增量训练的方法使得网络能够有效地逐步适应和学习复杂的问题。

级联相关网络的一个重要特点是它可以自动决定网络的结构和复杂度。网络会在训练过程中根据任务的需求动态地增加隐藏层神经元，从而适应更复杂的模式。

5.5.5Elman网络

Elman网络是一种递归神经网络（Recurrent Neural Network，RNN）结构，也称为简单循环神经网络（Simple Recurrent Neural Network）。它是一种具有反馈连接的前馈神经网络，用于处理序列数据和时序任务。
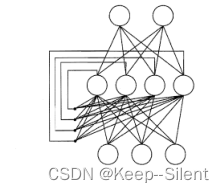
在这里插入图片描述

Elman网络的基本结构：

输入层：接收输入数据的神经元层。每个神经元表示输入序列中的一个元素或特征。
隐藏层：包含递归连接的神经元层。隐藏层的神经元将前一时刻的隐藏层输出作为输入，并结合当前时刻的输入数据进行计算。隐藏层的神经元可以捕捉到序列数据的时间依赖性和上下文信息。
输出层：根据隐藏层的输出计算得出网络的输出结果。输出层可以是分类器、回归器或其他适合特定任务的结构。
反馈连接：Elman网络的特点是在隐藏层中引入反馈连接。这些反馈连接将前一时刻的隐藏层输出反馈到当前时刻，使得网络能够捕捉到序列数据中的动态模式和时间相关性。

Elman网络在序列建模、语言模型、预测、语音识别和自然语言处理等任务中具有广泛的应用。它可以通过反向传播算法进行训练，也可以使用其他适当的优化算法进行参数更新。

5.5.6Boltzmann机

Boltzmann机（Boltzmann Machine）是一种基于概率的生成式神经网络模型。它由基本的随机二值神经元组成，这些神经元以随机方式相互连接，并使用能量函数进行训练和学习。
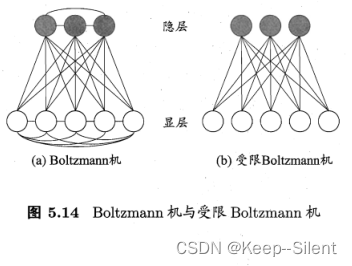
在这里插入图片描述
Boltzmann机的要点：

结构：Boltzmann机是一种全连接的无向图模型，其中的神经元被分为可见神经元（Visible Neurons）和隐藏神经元（Hidden Neurons）。可见神经元是外部输入的接收者，而隐藏神经元则进行内部信息的传递。
随机性：Boltzmann机中的神经元是随机二值神经元，其状态可以是0或1。每个神经元的输出由输入、权重和偏置的组合通过激活函数（通常是sigmoid函数）进行确定。
能量函数：Boltzmann机使用能量函数来定义模型的状态和参数。能量函数是一种衡量网络状态的度量，其中包括连接权重和神经元的状态。通过调整连接权重和偏置，网络可以自动学习模式和特征。
学习：Boltzmann机的学习过程是基于马尔可夫链的马尔可夫链蒙特卡洛方法（Markov Chain Monte Carlo，MCMC）进行的。使用对比散度（Contrastive Divergence）等算法进行参数的迭代更新，以最小化能量函数。
应用：Boltzmann机在许多领域中得到应用，包括特征学习、降维、生成模型、无监督学习等。它可以用于模式识别、图像处理、语音识别等任务。

需要注意的是，传统的Boltzmann机存在训练和计算复杂度高的问题。为了解决这些问题，出现了改进的变种，如受限玻尔兹曼机（Restricted Boltzmann Machine，RBM）和深度信念网络（Deep Belief Network，DBN），它们在Boltzmann机的基础上进行了简化和扩展。

5.6深度学习

深度学习（Deep Learning）是一种机器学习方法，旨在模仿人脑的神经网络结构和工作方式来处理和学习复杂的数据。深度学习通过构建深层次的神经网络模型，利用大量的数据进行训练，并自动学习数据的特征表示和抽象层次，从而实现高效的模式识别和数据分析。

深度学习的要点：

神经网络：深度学习的核心是神经网络模型，它由多个层次组成，包括输入层、隐藏层和输出层。隐藏层可以有多个，并且通常使用非线性激活函数（如ReLU、sigmoid等）来引入非线性特征。
深度结构：深度学习之所以称为深度学习，是因为它包含多个深层的隐藏层。深度结构使得网络能够学习到更抽象和高级的特征表示，从而提高模型的表达能力和性能。
自动特征学习：深度学习通过大量的数据和反向传播算法，自动学习数据的特征表示。网络根据误差信号和梯度下降的方法调整权重和偏置，以最小化预测误差并提高模型性能。
数据驱动：深度学习是一种数据驱动的方法，它依赖于大规模的标记数据来训练和优化模型。数据的质量和数量对深度学习的效果至关重要。
应用广泛：深度学习在众多领域取得了重大突破和广泛应用，包括计算机视觉、自然语言处理、语音识别、推荐系统等。它在图像分类、目标检测、机器翻译、智能助理等任务中取得了显著的成果。

深度学习的发展得益于算力的提升、数据的丰富和算法的创新。它已经成为人工智能领域的重要技术，并在许多实际问题中展现出强大的建模和预测能力。

5.7实验：手写数字识别

网络结构：
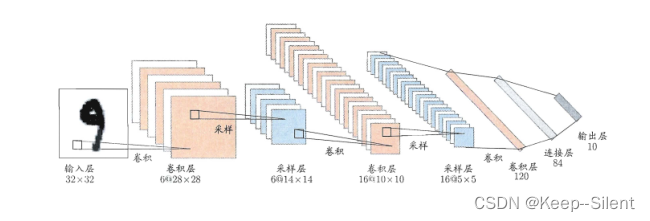
在这里插入图片描述
然而输入图不是32*32，是1*28*28，正确的网络结构应该是

level	input		stride	output
1	12828	655	1	62424
MaxPool	62424	MaxPool	2	61212
2	61212	1655	1	1688
MaxPool	1688	MaxPool	2	1644
Flatten	1644	Flatten		256
3FC	256	FC		120
4FC	120	FC		84
5FC	84	FC		10

# -*-coding =utf-8 -*-
import torch
import matplotlib.pyplot as plt
import torchvision

# 定义数据转换
transform = torchvision.transforms.Compose([
    torchvision.transforms.ToTensor(),
    torchvision.transforms.Normalize((0.1307,), (0.3081,))
])

# 加载数据集
batch_size=32
path = r'05data'
train_dataset = torchvision.datasets.MNIST(root=path, train=True,transform=transform,download =False)
train_loader = torch.utils.data.DataLoader(train_dataset, batch_size=batch_size, shuffle=True)
test_dataset = torchvision.datasets.MNIST(root=path, train=True,transform=transform,download =False)
test_loader = torch.utils.data.DataLoader(test_dataset, batch_size=batch_size, shuffle=True)
# loader.shape=1875*[32*1*28*28,32]

# 数据集可视化
from sklearn.preprocessing import MinMaxScaler
# 归一化转为[0,255]
transfer=MinMaxScaler(feature_range=(0, 255)) 
def visualize_loader(batch,predicted=''): 
    # batch=[32*1*28*28,32]
    imgs=batch[0].squeeze().numpy() # 消squeeze()一维
    fig, axes = plt.subplots(4, 8, figsize=(12, 6))
    labels=batch[1].numpy()
    if str(predicted)=='':
        predicted=labels
    for i, ax in enumerate(axes.flat):
        ax.imshow(imgs[i])
        ax.set_title(predicted[i],color='black' if predicted[i]==labels[i] else 'red')
        ax.axis('off')
    plt.tight_layout()
    plt.show()


# loader.shape=1875*[32*1*28*28,32]
for batch in train_loader:       
    break
visualize_loader(batch)

在这里插入图片描述

在PyTorch的torch.nn模块中，卷积函数Conv2d的输入张量的形状应为[batch_size, channels, height, width]对应数据集，无需修改。

# 创建模型
import torch
import torch.nn as nn
import torch.optim as optim

# 定义模型
class CNN(nn.Module):
    def __init__(self):
        super(CNN, self).__init__()
        self.conv1 = nn.Conv2d(1, 6, kernel_size=5, stride=1)
        self.relu = nn.ReLU()
        self.maxpool = nn.MaxPool2d(kernel_size=2, stride=2)
        self.conv2 = nn.Conv2d(6, 16, kernel_size=5, stride=1)
        self.flatten=nn.Flatten()
        self.fc3 = nn.Linear(256, 120)
        self.fc4 = nn.Linear(120, 84)
        self.fc5 = nn.Linear(84, 10)

    def forward(self, x):
        x = self.conv1(x)
        x = self.relu(x)
        x = self.maxpool(x)
        x = self.conv2(x)
        x = self.relu(x)
        x = self.maxpool(x)
        x = self.flatten(x)
        x = self.fc3(x)
        x = self.relu(x)
        x = self.fc4(x)
        x = self.relu(x)
        x = self.fc5(x)
        return x

# 打印模型结构
model = CNN()
print(model)

CNN(
  (conv1): Conv2d(1, 6, kernel_size=(5, 5), stride=(1, 1))
  (relu): ReLU()
  (maxpool): MaxPool2d(kernel_size=2, stride=2, padding=0, dilation=1, ceil_mode=False)
  (conv2): Conv2d(6, 16, kernel_size=(5, 5), stride=(1, 1))
  (flatten): Flatten(start_dim=1, end_dim=-1)
  (fc3): Linear(in_features=256, out_features=120, bias=True)
  (fc4): Linear(in_features=120, out_features=84, bias=True)
  (fc5): Linear(in_features=84, out_features=10, bias=True)
)

import torch.optim as optim

num_epochs=1
device = torch.device("cuda" if torch.cuda.is_available() else "cpu")
model.to(device)
criterion = nn.CrossEntropyLoss()
optimizer = optim.Adam(model.parameters(), lr=0.001)

for epoch in range(num_epochs):
    model.train()
    running_loss = 0.0
    correct = 0
    total = 0
    
    for images, labels in train_loader:
        images = images.to(device)
        labels = labels.to(device)
        
        # 前向传播
        outputs = model(images)
        loss = criterion(outputs, labels)
        
        # 反向传播和优化
        optimizer.zero_grad()
        loss.backward()
        optimizer.step()
        
        # 统计准确率
        _, predicted = torch.max(outputs.data, 1)
        total += labels.size(0)
        correct += (predicted == labels).sum().item()
        
        running_loss += loss.item()
    
    train_loss = running_loss / len(train_loader)
    train_accuracy = correct / total
    
    # 在测试集上评估模型
    model.eval()
    test_loss = 0.0
    correct = 0
    total = 0
    
    with torch.no_grad():
        for images, labels in test_loader:
            images = images.to(device)
            labels = labels.to(device)
            
            outputs = model(images)
            loss = criterion(outputs, labels)
            
            _, predicted = torch.max(outputs.data, 1)
            total += labels.size(0)
            correct += (predicted == labels).sum().item()
            
            test_loss += loss.item()
    
    test_loss = test_loss / len(test_loader)
    test_accuracy = correct / total
    
    # 打印训练过程中的损失和准确率
    print(f"Epoch [{epoch+1}/{num_epochs}] - Train Loss: {train_loss:.4f}, Train Accuracy: {train_accuracy:.4f}, Test Loss: {test_loss:.4f}, Test Accuracy: {test_accuracy:.4f}")

Epoch [1/1] - Train Loss: 0.0154, Train Accuracy: 0.9951, Test Loss: 0.0109, Test Accuracy: 0.9964

#保存模型
#torch.save(model.state_dict(), '05model.pth')

# 创建一个新的模型实例
model = CNN()
# 加载模型的参数
model.load_state_dict(torch.load('05model.pth'))

# 测试
for batch in test_loader:       
    break
imgs=batch[0]
outputs = model(imgs)
_, predicted = torch.max(outputs.data, 1)
predicted=predicted.numpy()

print(predicted)

visualize_loader(batch,predicted)