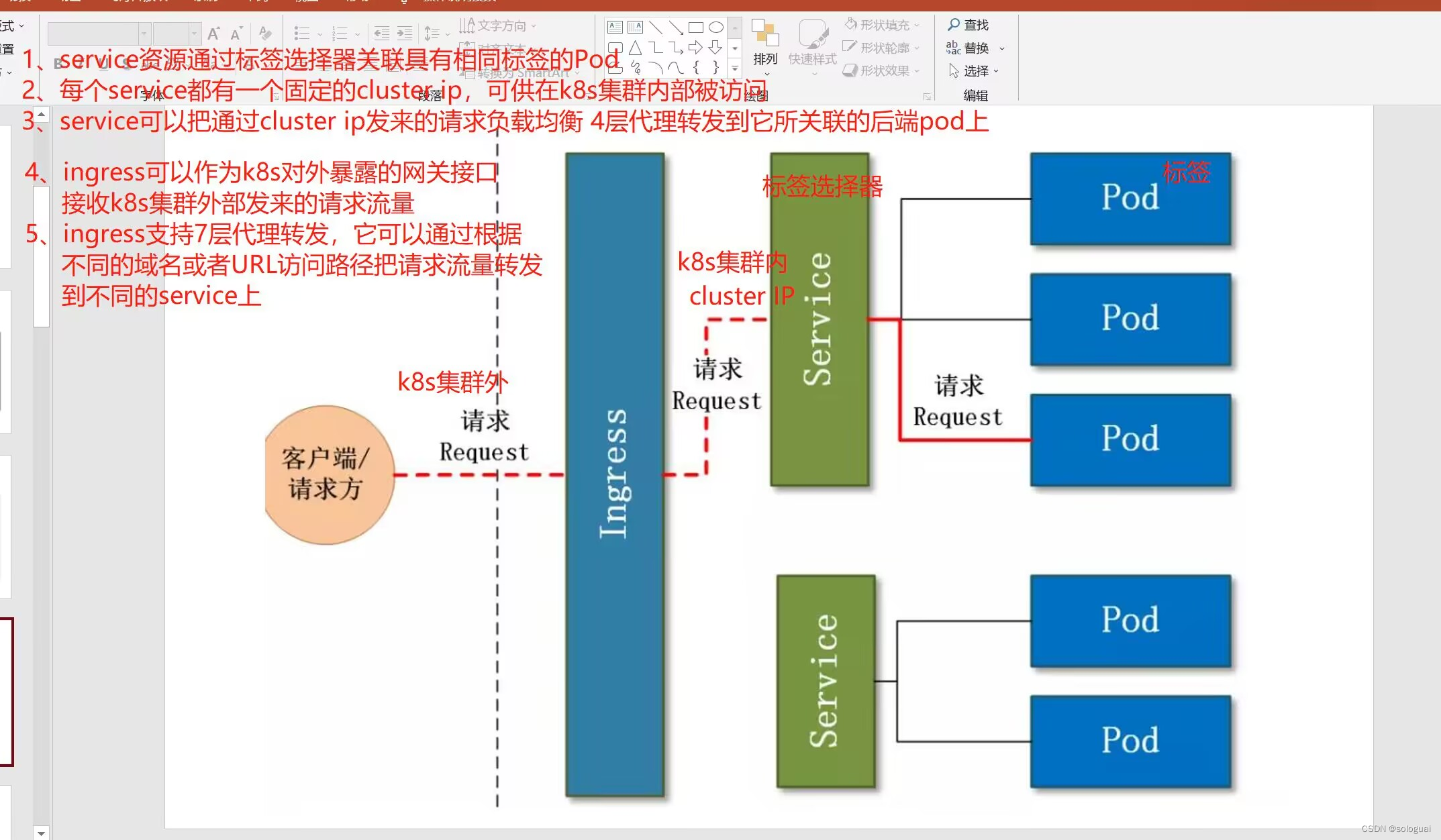
这个专栏主要是用来分享一下我在机器学习中的学习笔记及一些感悟，也希望对你的学习有帮助哦！感兴趣的小伙伴欢迎私信或者评论区留言！这一篇就更新一下《白话机器学习中的数学——多项式回归》！

目录

一、什么多项式回归

二、算法分析

三、总结

---

一、什么多项式回归

多项式回归是线性回归的一种特殊情况，其中我们在数据上拟合了多项式方程，目标变量和自变量之间具有曲线关系。 在曲线关系中，目标变量的值相对于预测变量以不均匀的方式变化。

二、算法分析

首先我们看一次函数的解析式：

我们引入了两个变量，和，它的图像是一条直线:

 之前我们用微分求出了这个函数的斜率和截距，但是从我们的数据点上来看，其实曲线比 直线拟合得更好。

我们将fθ(x)定义为二次函数，添加一个二次项，就能用它来表示这条曲线了。

或者我们用更高次次数的表达式也可以。这样就能表示更复杂的曲线了。

 所以我们在不断尝试之后决定是什么样的函数，但是要注意，并不是函数次数越大，拟合得越好。次数过大，难免会出现过拟合的情况。首先我们先看加入这个新的函数。接下来我们写出更新表达式的推导方法。

和之前一样，设u = E(θ)、v = fθ(x)，然后试着用 u 对 θ2偏微分，求出更新表达式。u 对 v 微分的部分是一样的，所以我们只要求 v 对 θ2 的微分就行了。

那么即使增加参数，比如有 θ3、θ4 等，我们依然可以用同样的方法求出它们的更新表达式，像这样增加函数中多项式的次数，然后再使用函数的分析方法就被称为多项式回归！

三、总结

多项式回归在原有的基础上引入了更高次的变量，我们要求出更高次参数的更新表达式，这一部分可以看之前写的梯度下降法更新参数。只要求出参数就能求得表达式了。