飞行动力学 - 第5节-part3-爬升性能随高度的变化趋势 之 基础点摘要
- 1. 动力学方程
- 2. 爬升角、爬升率趋势
- 3. 参考资料
1. 动力学方程
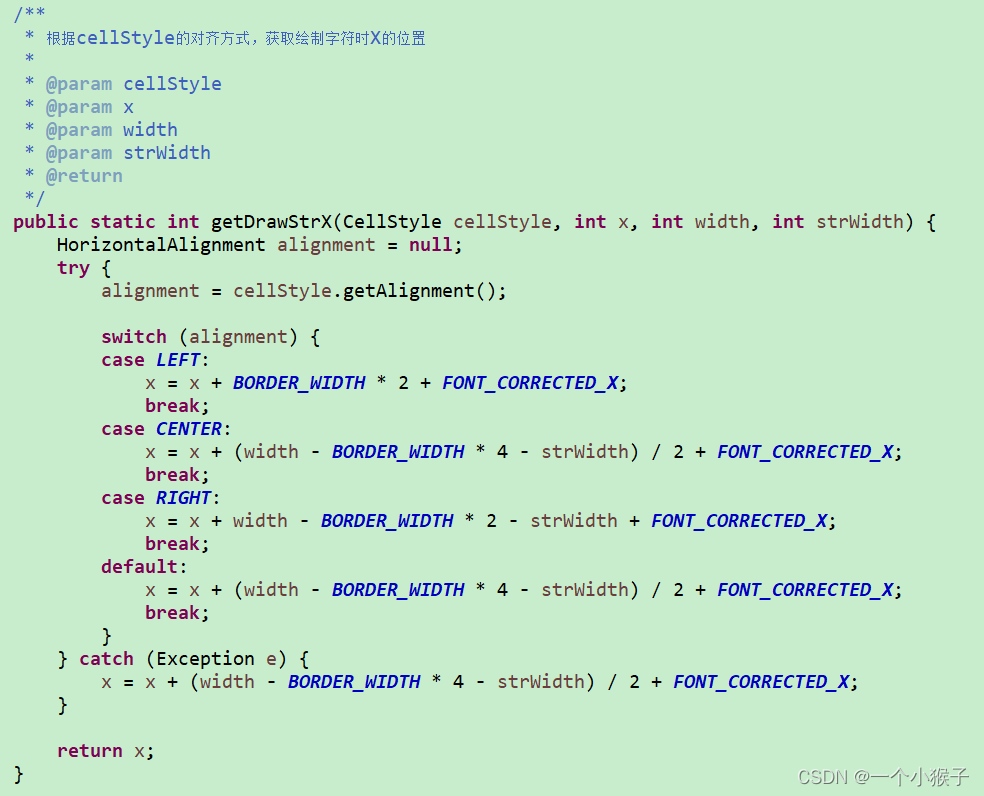
回顾下,根据牛顿第一运动定律给出的动力学方程:
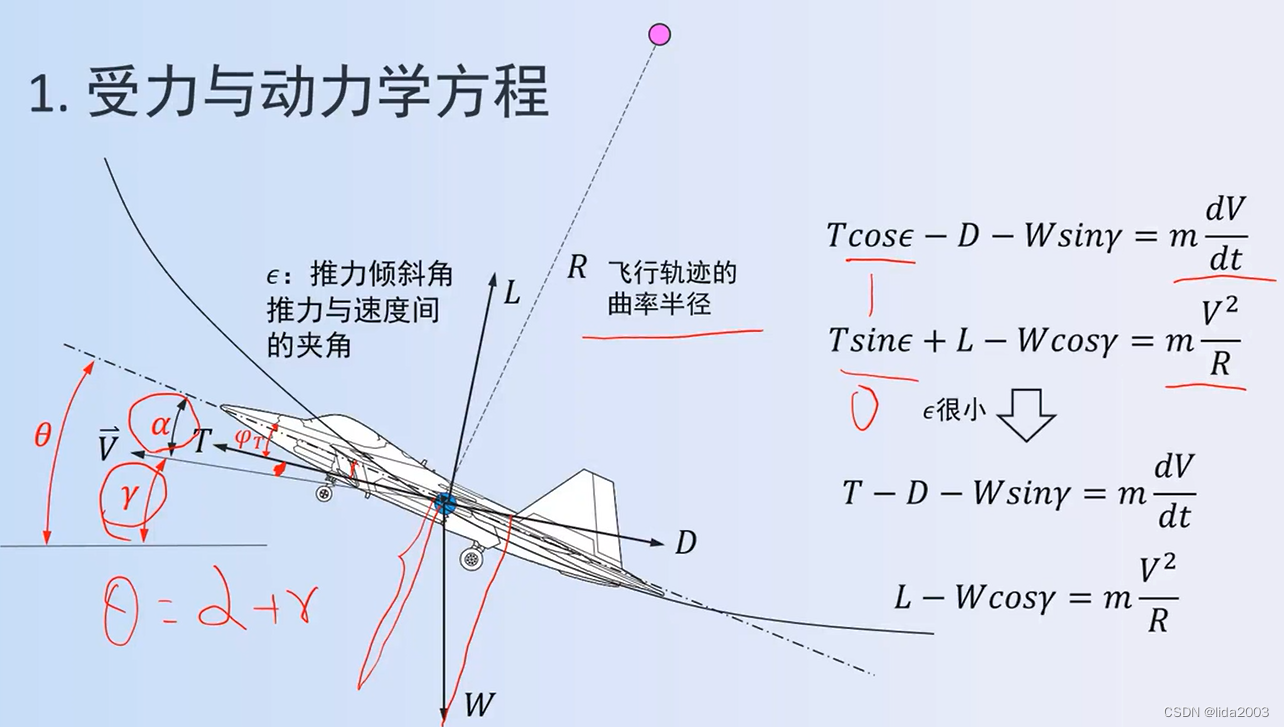
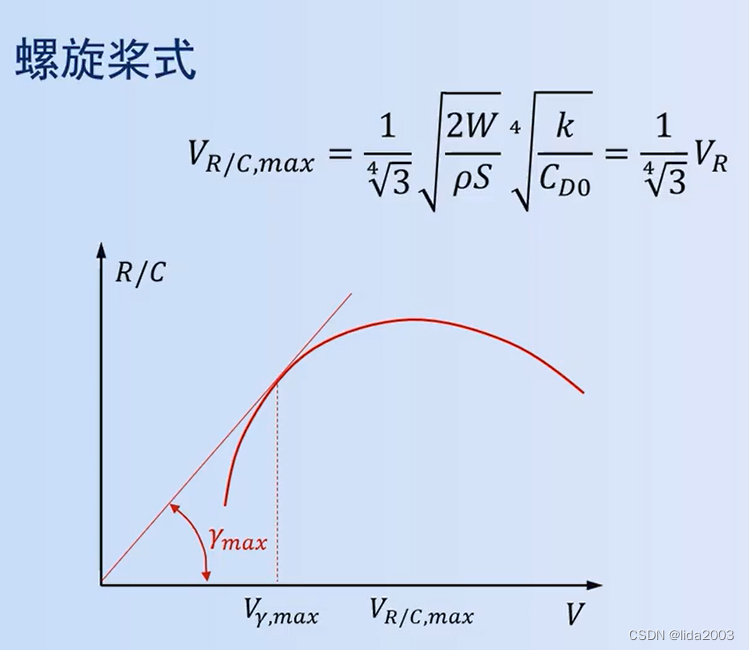
2. 爬升角、爬升率趋势
从推导公式的角度,上述趋势需要考虑以下几个因素:
- 高度
- 空气密度
- 发动机推力
- 发动机功率
大致有以下几个逻辑关系(维持其他因素,改变其中一个因素)
- 高度越高,空气密度越小
- 高度越高,喷气飞机推力越小
- 高度越高,螺旋桨飞机功率越小
- 最小所需功率/推力后,随速度增加所需功率增加
物理逻辑就是牛顿三大定律:
- 牛顿第一运动定律:在没有外力作用下孤立质点保持静止或做匀速直线运动
- 牛顿第二运动定律:动量为P的质点,在外力F的作用下,其动量随时间的变化率同该质点所受的外力成正比,并与外力的方向相同
- 牛顿第三运动定律:相互作用的两个质点之间的作用力和反作用力总是大小相等,方向相反,作用在同一条直线上
在飞行动力学 - 第1节-课程简介、飞行性能概念 之 基础点摘要就已经明确通过惯性定律推导除了飞行动力学方程。
在此基础上,当所需功率/推力最小的时候,爬升率或者爬升角才有极值的可能。

3. 参考资料
飞行动力学-第5节-part3-爬升性能随高度的变化趋势