题目1：组合

给定两个整数 n 和 k，返回范围 [1, n] 中所有可能的 k 个数的组合。

你可以按 任何顺序 返回答案。

输入：n = 4, k = 2
输出：
[
  [2,4],
  [3,4],
  [2,3],
  [1,2],
  [1,3],
  [1,4],
]

 解题思路：

1.定义一个temp数组，存放临时的组合结果

2.两种选择：1.选择当前元素2.不选择当前元素

3.注意递归结束条件：当temp的长度加上[cur,n]区间的长度小于k时，一定构不成k个数的组合，此时return

源代码如下：

class Solution {
public:
    vector<vector<int>> res;
    vector<int> temp;
    void dfs(int cur,int n,int k)
    {
        //当temp的长度加上[cur,n]区间的长度小于k时，一定构不成k个数的组合，所以直接return
        if(temp.size()+(n-cur+1)<k)
        {
            return;
        }
        //当temp长度等于k时，说明这是组合中的其中一个，将temp存放到res中 
        if(temp.size()==k)
        {
            res.push_back(temp);
            return;
        }
        //选择当前的数
        temp.push_back(cur);
        dfs(cur+1,n,k);
        //回溯
        temp.pop_back();
        //不选择当前的位置
        dfs(cur+1,n,k);
    }
    vector<vector<int>> combine(int n, int k) {
        dfs(1,n,k);
        return res;
    }
};

题目2：单词搜索

给定一个 m x n 二维字符网格 board 和一个字符串单词 word 。如果 word 存在于网格中，返回 true ；否则，返回 false 。

单词必须按照字母顺序，通过相邻的单元格内的字母构成，其中“相邻”单元格是那些水平相邻或垂直相邻的单元格。同一个单元格内的字母不允许被重复使用。

示例：

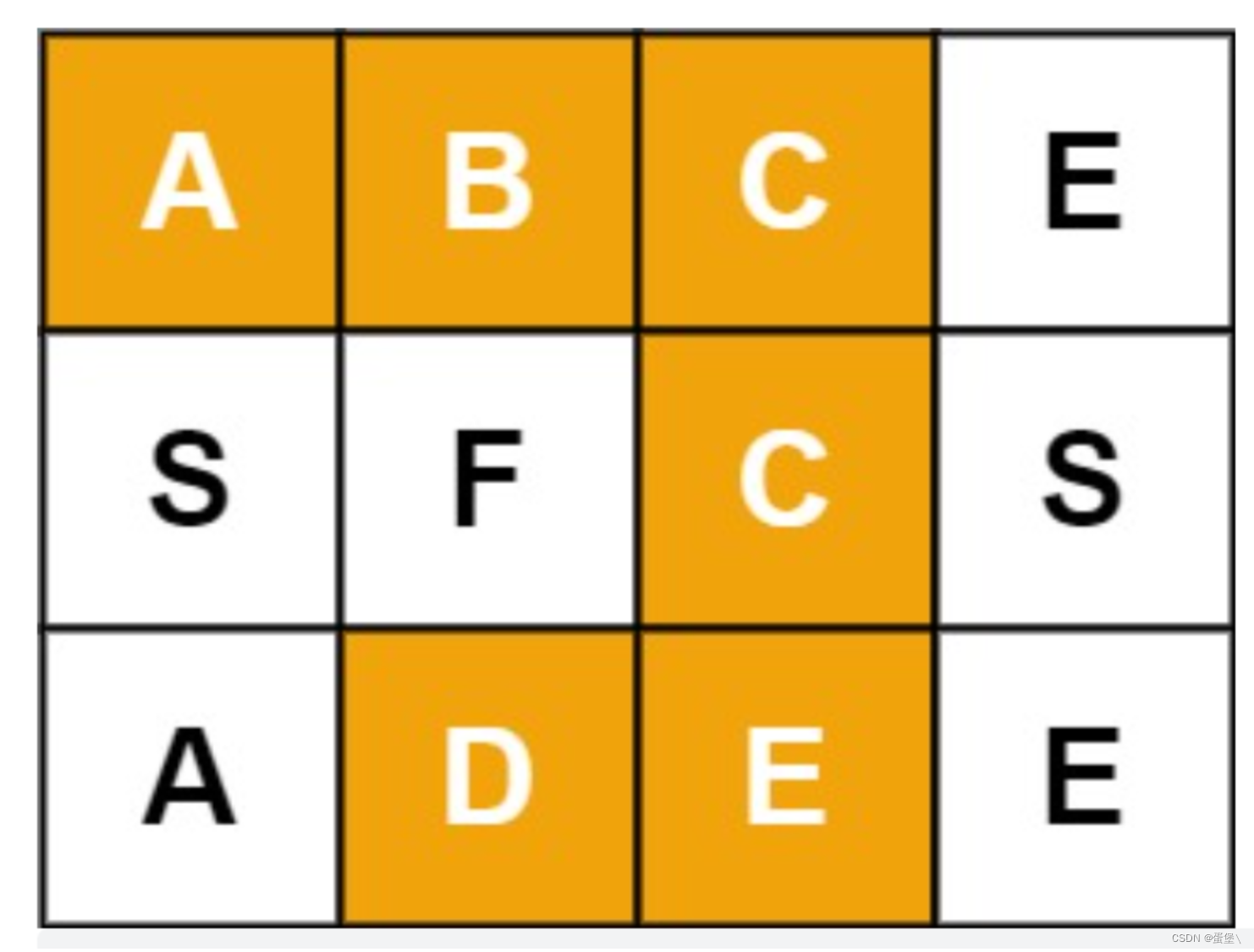
 输入：board = [["A","B","C","E"],["S","F","C","S"],["A","D","E","E"]], word = "ABCCED"
输出：true
输入：board = [["A","B","C","E"],["S","F","C","S"],["A","D","E","E"]], word = "ABCB"
输出：false

解题思路：
本题采用递归回溯来实现

1.设置一个二维数组mark，用来标记矩阵中的元素是否被使用 

2.对矩阵中的每一个元素都进行递归，找能够连续起来的单词

3.注意停止递归的条件（下标越界、元素已被使用、当前元素不等于单词的当前字符）

4.回溯时，要将单词重新标记为未被使用

源代码如下：

class Solution {
public:
    bool dfs(int i,int j,int k,vector<vector<char>>& board, string word,vector<vector<bool>>& mark)
    {
        //i和j越界时，返回false
        if(i<0||i>=board.size()||j<0||j>=board[0].size()) return false;
        //当前下标的元素被使用过或者当前元素不等于单词的当前字符，返回false
        if(mark[i][j]||board[i][j]!=word[k]) return false;
        //当k已经遍历到单词的最后一个字符，且前面两个情况都不符合，那么说明在矩阵中找到了该单词
        if(k==word.size()-1) return true;
        //将当前元素标记为已使用
        mark[i][j]=true;
        //继续递归当前元素的上下左右元素，任意一个方向能找到都可以
        if(dfs(i-1,j,k+1,board,word,mark)||
        dfs(i+1,j,k+1,board,word,mark)||
        dfs(i,j-1,k+1,board,word,mark)||
        dfs(i,j+1,k+1,board,word,mark))
        {
            return true;
        }
        //回溯，将元素标记为未使用
        mark[i][j]=false;
        return false;
        
    }
    bool exist(vector<vector<char>>& board, string word) {
        int m=board.size();//矩阵的行
        int n=board[0].size();//矩阵的列
        //用来标记元素的使用情况，true表示已被使用、false表示未被使用
        vector<vector<bool>> mark(m,vector<bool>(n,false));
        //遍历递归矩阵中的所有元素，直到找到单词为止
       for(int i=0;i<m;i++)
       {
           for(int j=0;j<n;j++)
           {
               if(dfs(i,j,0,board,word,mark))
               {
                   return true;
               }
           }
       }
        //找不到，返回false
       return false;
    }
};