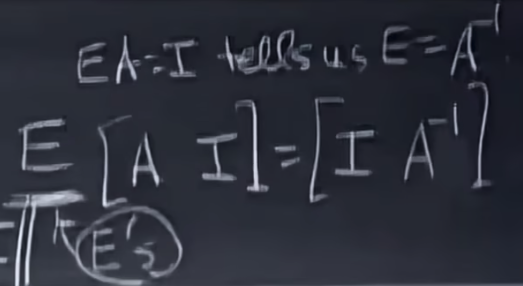x.1 矩阵乘法

矩阵乘法的常用运算规则有五种，如下是一种，是最简单的矩阵乘法，用一行乘以一列，假设A是mxn的矩阵，B是nxp的矩阵，则最终得到mxp的矩阵。

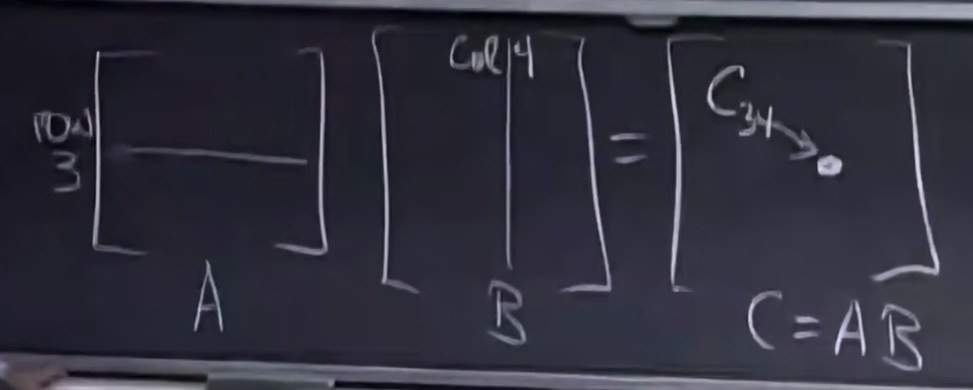
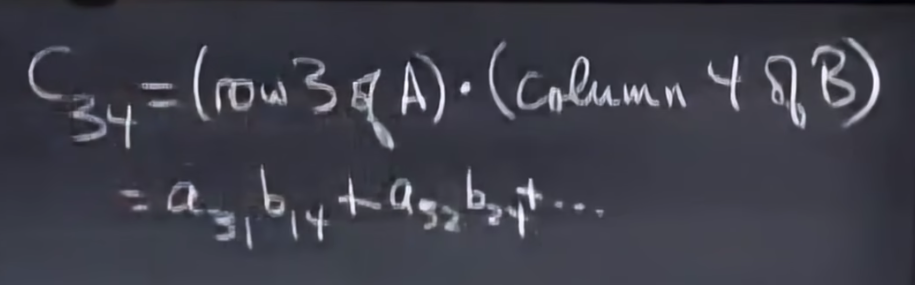
在矩阵A和向量a乘法中，我们已经习惯性地将矩阵A分解为与向量a相匹配的行向量或列向量的组合，再将向量a看做分解后行/列向量的线性组合。现在对于矩阵乘矩阵，我们同样可以进行分解，将其看做线性组合，我们可以进行行分解和列分解，于是又多了两种矩阵乘法的理解思路，如下，

将矩阵的一列乘以一行，得到秩为1的矩阵。

将矩阵进行分块，再相乘，叫做block multiplication分块乘法。

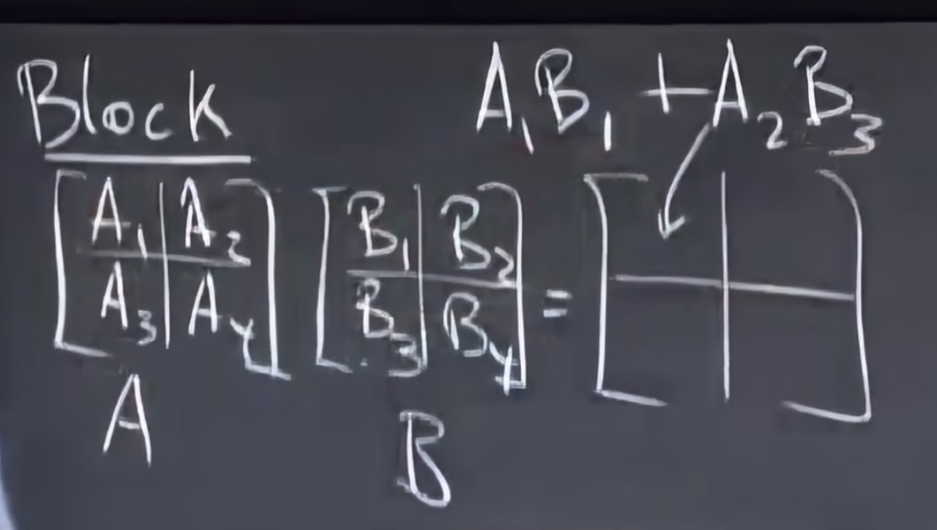
x.2 矩阵的逆

如果A存在A-1则有：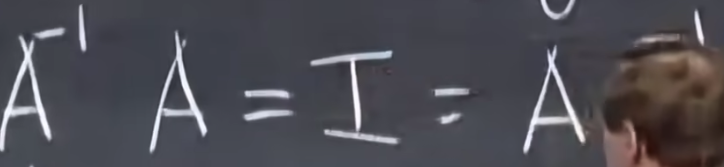

如果上面的式子成立，则我们称A是invertible可逆或者non-singular非奇异的。可逆矩阵是good矩阵，不可逆不good。

那么如何判断一个矩阵A是否可逆呢，可以通过行列式等于0则矩阵不可逆，但我们更喜欢用克莱姆法则，如果你能找到一个非零向量使得Ax=0成立，则矩阵A不可逆。

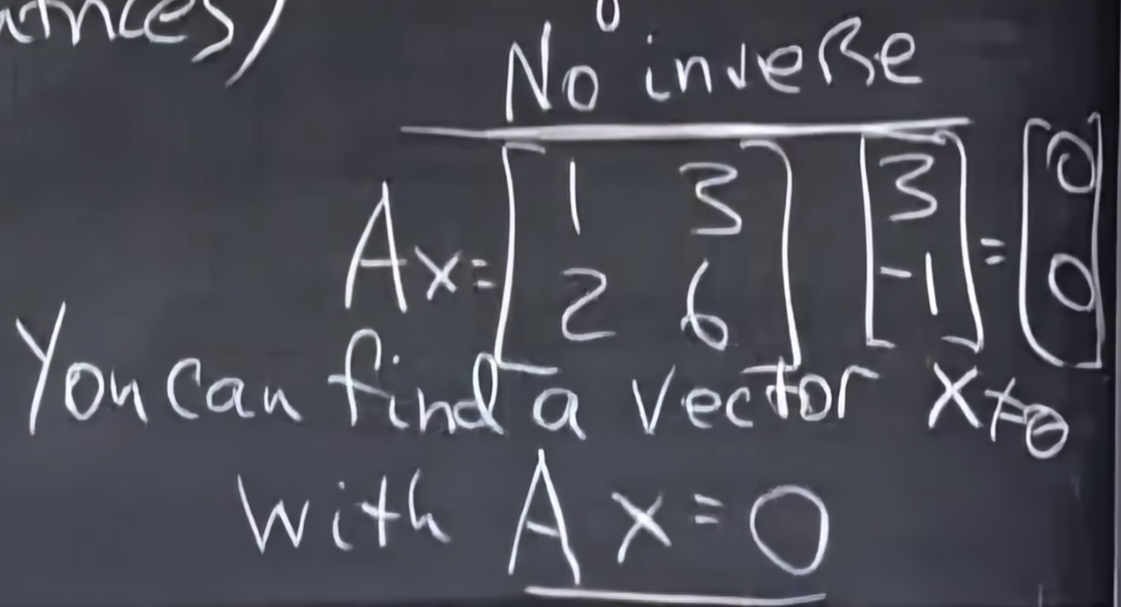
但是当矩阵A是可逆时，如何求解A的逆呢？通过将A列分解成两个列向量[1, 2], [3, 7]我们很容易观察到这两个向量不共线，A是易于证明的可逆矩阵。

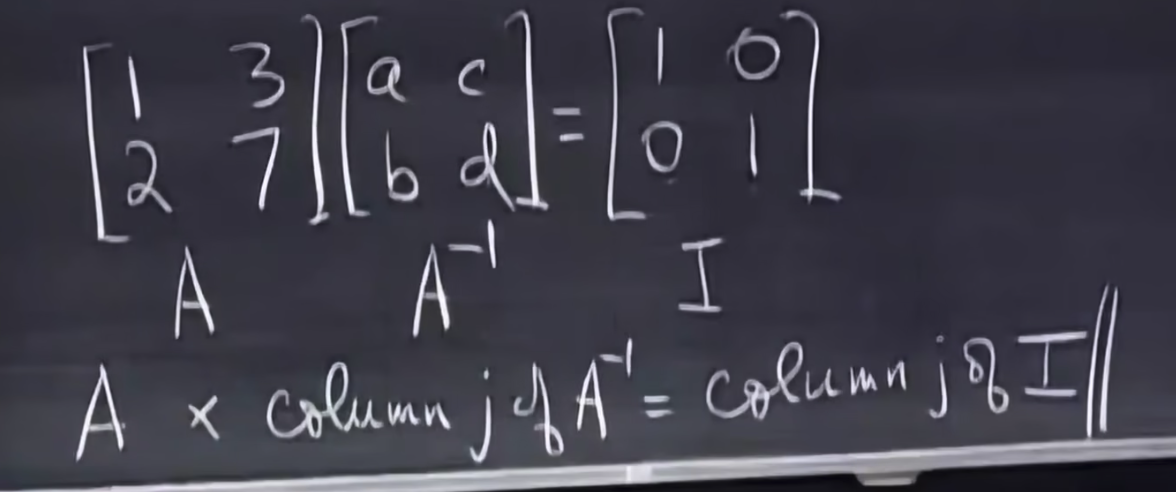
我们引入Gauss-Jordan来求解逆矩阵。即将上面的式子看做两个方程组进行求解[a, b]和[c, d]，如下所示，

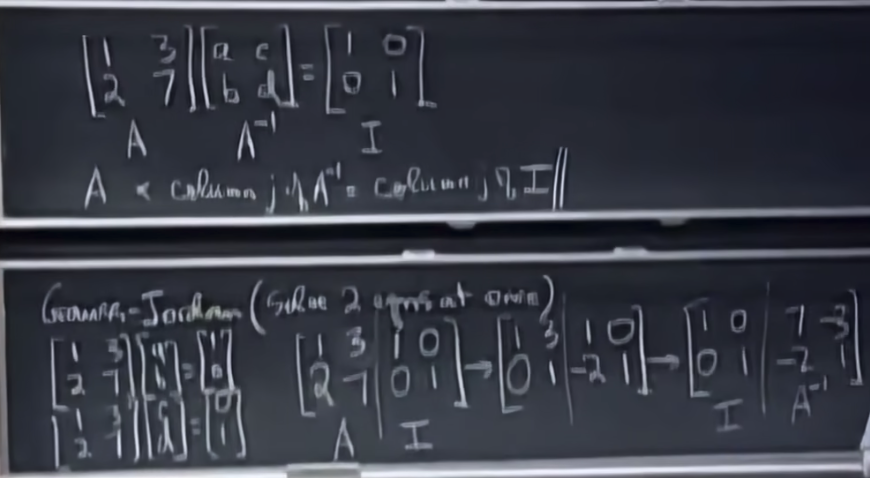
那么如何证明Gauss-Jordan的合理性呢，我们引入初等矩阵进行解释。我们对[A|I]进行行变换的本质是对[A|I]的左侧疯狂乘初等矩阵，所以最终根据乘法结合律将这些乘的初等矩阵相乘，就得到了A逆，证明如下，