机器学习16：使用 TensorFlow 进行神经网络编程练习

news2024/11/18 9:42:09

在【机器学习15】中，笔者介绍了神经网络的基本原理。在本篇中，我们使用 TensorFlow 来训练、验证神经网络模型，并探索不同 “层数+节点数” 对模型预测效果的影响，以便读者对神经网络模型有一个更加直观的认识。

目录

1.导入依赖模块

2.加载数据集

3.表示数据

4.构建线性回归模型-作为基线

4.1 定义损失打印函数

4.2 定义函数以创建和训练线性回归模型

4.3 定义线性回归模型输出

4.4 调用函数训练、测试模型

4.5 完整代码运行

5.深度神经网络模型

5.1 定义深度神经网络（DNN）模型

5.2 调用函数来构建和训练深度神经网络

5.3 优化深度神经网络的拓扑结构

5.3.1 实验一：增加层数

5.3.2 实验一：减少节点数

6.两种模型结果对比

7.参考文献

1.导入依赖模块

相较于前面的系列文章，需要新增一个模块 seaborn。可以通过 PyCharm 的图形化工具安装，也可以通过命令“pip3 install --index-url https://mirrors.aliyun.com/pypi/simple/ seaborn” 直接安装。

import numpy as np
import pandas as pd
import tensorflow as tf
from matplotlib import pyplot as plt
import seaborn as sns

# The following lines adjust the granularity of reporting.
pd.options.display.max_rows = 10
pd.options.display.float_format = "{:.1f}".format

2.加载数据集

本案例中采用的数据集原始地址为如下：

  • 训练数据：https://download.mlcc.google.com/mledu-datasets/california_housing_train.csv
  • 测试数据：https://download.mlcc.google.com/mledu-datasets/california_housing_test.csv

我们需要将上述数据下载到本地，然后将其路径（数据文件在你电脑的实际路径）写入代码中，如下代码所示：

# 载入数据集
train_df = pd.read_csv("/Users/jinKwok/Downloads/california_housing_train.csv")
test_df = pd.read_csv("/Users/jinKwok/Downloads/california_housing_test.csv")
# 打乱训练数据示例
train_df = train_df.reindex(np.random.permutation(train_df.index))

3.表示数据

以下代码单元创建输出三个特征的预处理层：

  • cross_latitude_longitude：纬度 X 经度（特征交叉）

  • median_income：收入中位数；

  • population：人口

其中指定了最终用于训练模型的特征，以及这些特征的表示形式。在向转换传递 DataFrame 之前，转换（收集在 presecuring_layers 中）实际上不会被应用，在我们训练模型时才会真正被应用。我们将对线性回归模型和神经网络模型使用预处理层。

# Keras 构建浮点值输入张量
inputs = {
    'latitude':
        tf.keras.layers.Input(shape=(1,), dtype=tf.float32,
                              name='latitude'),
    'longitude':
        tf.keras.layers.Input(shape=(1,), dtype=tf.float32,
                              name='longitude'),
    'median_income':
        tf.keras.layers.Input(shape=(1,), dtype=tf.float32,
                              name='median_income'),
    'population':
        tf.keras.layers.Input(shape=(1,), dtype=tf.float32,
                              name='population')
}

# 创建一个规范化（归一化）层来规范 median_income 数据
median_income = tf.keras.layers.Normalization(
    name='normalization_median_income',
    axis=None)
median_income.adapt(train_df['median_income'])
median_income = median_income(inputs.get('median_income'))

# 创建一个规范化（归一化）层来规范 population 数据
population = tf.keras.layers.Normalization(
    name='normalization_population',
    axis=None)
population.adapt(train_df['population'])
population = population(inputs.get('population'))

# 创建一个数字列表，表示纬度分桶的边界。
# 因为我们使用的是归一化层，所以纬度和经度的值将在大约-3到3的范围内（表示Z分数）。
# 我们将创建20个bucket（桶），这需要21个bucket边界（因此是20+1）。
latitude_boundaries = np.linspace(-3, 3, 20 + 1)

# 创建一个规范化（归一化）层来规范 latitude-纬度 数据
latitude = tf.keras.layers.Normalization(
    name='normalization_latitude',
    axis=None)
latitude.adapt(train_df['latitude'])
latitude = latitude(inputs.get('latitude'))

# 创建一个离散化层，将纬度数据分离存储到桶中
latitude = tf.keras.layers.Discretization(
    bin_boundaries=latitude_boundaries,
    name='discretization_latitude')(latitude)

# 创建一个数字列表，表示经度分桶的边界
longitude_boundaries = np.linspace(-3, 3, 20 + 1)

# 创建一个规范化（归一化）层来规范 longitude-经度 数据
longitude = tf.keras.layers.Normalization(
    name='normalization_longitude',
    axis=None)
longitude.adapt(train_df['longitude'])
longitude = longitude(inputs.get('longitude'))

# 创建一个离散化层，将经度数据分离存储到桶中。
longitude = tf.keras.layers.Discretization(
    bin_boundaries=longitude_boundaries,
    name='discretization_longitude')(longitude)

# 将经纬度特征交叉成一个单一的热向量
feature_cross = tf.keras.layers.HashedCrossing(
    # num_bins 可以调整：值越高，精度越高；值越低，性能越高。
    num_bins=len(latitude_boundaries) * len(longitude_boundaries),
    output_mode='one_hot',
    name='cross_latitude_longitude')([latitude, longitude])

# 将我们的输入连接到一个张量中
preprocessing_layers = tf.keras.layers.Concatenate()(
    [feature_cross, median_income, population])

4.构建线性回归模型-作为基线

4.1 定义损失打印函数

# 定义损失曲线打印函数
def plot_the_loss_curve(epochs, mse_training, mse_validation):
    """打印损失和训练轮次的关系图"""
    plt.figure()
    plt.xlabel("Epoch")
    plt.ylabel("Mean Squared Error")

    plt.plot(epochs, mse_training, label="Training Loss")
    plt.plot(epochs, mse_validation, label="Validation Loss")

    # 由于mse_training是pandas系列，所以需先将其转换为列表
    merged_mse_lists = mse_training.tolist() + mse_validation
    highest_loss = max(merged_mse_lists)
    lowest_loss = min(merged_mse_lists)
    top_of_y_axis = highest_loss * 1.03
    bottom_of_y_axis = lowest_loss * 0.97

    plt.ylim([bottom_of_y_axis, top_of_y_axis])
    plt.legend()
    plt.show()

4.2 定义函数以创建和训练线性回归模型

# 定义线性回归模型创建函数
def create_model(my_inputs, my_outputs, my_learning_rate):
    model = tf.keras.Model(inputs=my_inputs, outputs=my_outputs)
    # 将层构造为TensorFlow可以执行的模型
    model.compile(optimizer=tf.keras.optimizers.Adam(
        learning_rate=my_learning_rate),
        loss="mean_squared_error",
        metrics=[tf.keras.metrics.MeanSquaredError()])

    return model


# 创建规范化层以归一化median_house_value数据。
# 因为median_house_value是我们的标签（即我们预测的目标值），所以这些层不会添加到我们的模型中
train_median_house_value_normalized = tf.keras.layers.Normalization(axis=None)
train_median_house_value_normalized.adapt(
    np.array(train_df['median_house_value']))

test_median_house_value_normalized = tf.keras.layers.Normalization(axis=None)
test_median_house_value_normalized.adapt(
    np.array(test_df['median_house_value']))


# 定义模型训练函数
def train_model(model, dataset, epochs, batch_size, label_name, validation_split=0.1):
    """将数据灌入模型以对其进行训练"""
    # 将数据集拆分为特征和标签
    features = {name: np.array(value) for name, value in dataset.items()}
    label = train_median_house_value_normalized(
        np.array(features.pop(label_name)))
    history = model.fit(x=features, y=label, batch_size=batch_size,
                        epochs=epochs, shuffle=True, validation_split=validation_split)

    # 获取有助于绘制损失曲线的详细信息
    epochs = history.epoch
    hist = pd.DataFrame(history.history)
    mse = hist["mean_squared_error"]

    return epochs, mse, history.history

4.3 定义线性回归模型输出

# 定义线性回归模型模型输出
def get_outputs_linear_regression():
    # 创建密集输出层
    dense_output = tf.keras.layers.Dense(units=1, input_shape=(1,),
                                         name='dense_output')(preprocessing_layers)

    # 定义一个输出字典，并发送给模型构造函数
    outputs = {
        'dense_output': dense_output
    }
    return outputs

4.4 调用函数训练、测试模型

# 设置超参数
learning_rate = 0.01
epochs = 15
batch_size = 1000
label_name = "median_house_value"

# 将原始训练集拆分为训练集和验证集
validation_split = 0.2

outputs = get_outputs_linear_regression()

# 构建模型拓扑
my_model = create_model(inputs, outputs, learning_rate)

# 基于规范化后的训练集数据训练模型
epochs, mse, history = train_model(my_model, train_df, epochs, batch_size,
                                   label_name, validation_split)
plot_the_loss_curve(epochs, mse, history["val_mean_squared_error"])

test_features = {name: np.array(value) for name, value in test_df.items()}
test_label = test_median_house_value_normalized(test_features.pop(label_name))  # isolate the label
print("\n Evaluate the linear regression model against the test set:")
my_model.evaluate(x=test_features, y=test_label, batch_size=batch_size, return_dict=True)

4.5 完整代码运行

import numpy as np
import pandas as pd
import tensorflow as tf
from matplotlib import pyplot as plt
import seaborn as sns

# The following lines adjust the granularity of reporting.
pd.options.display.max_rows = 10
pd.options.display.float_format = "{:.1f}".format

print("Imported modules.")

# 载入数据集
train_df = pd.read_csv("/Users/jinKwok/Downloads/california_housing_train.csv")
test_df = pd.read_csv("/Users/jinKwok/Downloads/california_housing_test.csv")
# 打乱训练数据示例
train_df = train_df.reindex(np.random.permutation(train_df.index))

# Keras 构建浮点值输入张量
inputs = {
    'latitude':
        tf.keras.layers.Input(shape=(1,), dtype=tf.float32,
                              name='latitude'),
    'longitude':
        tf.keras.layers.Input(shape=(1,), dtype=tf.float32,
                              name='longitude'),
    'median_income':
        tf.keras.layers.Input(shape=(1,), dtype=tf.float32,
                              name='median_income'),
    'population':
        tf.keras.layers.Input(shape=(1,), dtype=tf.float32,
                              name='population')
}

# 创建一个规范化（归一化）层来规范 median_income 数据
median_income = tf.keras.layers.Normalization(
    name='normalization_median_income',
    axis=None)
median_income.adapt(train_df['median_income'])
median_income = median_income(inputs.get('median_income'))

# 创建一个规范化（归一化）层来规范 population 数据
population = tf.keras.layers.Normalization(
    name='normalization_population',
    axis=None)
population.adapt(train_df['population'])
population = population(inputs.get('population'))

# 创建一个数字列表，表示纬度分桶的边界。
# 因为我们使用的是归一化层，所以纬度和经度的值将在大约-3到3的范围内（表示Z分数）。
# 我们将创建20个bucket（桶），这需要21个bucket边界（因此是20+1）。
latitude_boundaries = np.linspace(-3, 3, 20 + 1)

# 创建一个规范化（归一化）层来规范 latitude-纬度 数据
latitude = tf.keras.layers.Normalization(
    name='normalization_latitude',
    axis=None)
latitude.adapt(train_df['latitude'])
latitude = latitude(inputs.get('latitude'))

# 创建一个离散化层，将纬度数据分离存储到桶中
latitude = tf.keras.layers.Discretization(
    bin_boundaries=latitude_boundaries,
    name='discretization_latitude')(latitude)

# 创建一个数字列表，表示经度分桶的边界
longitude_boundaries = np.linspace(-3, 3, 20 + 1)

# 创建一个规范化（归一化）层来规范 longitude-经度 数据
longitude = tf.keras.layers.Normalization(
    name='normalization_longitude',
    axis=None)
longitude.adapt(train_df['longitude'])
longitude = longitude(inputs.get('longitude'))

# 创建一个离散化层，将经度数据分离存储到桶中。
longitude = tf.keras.layers.Discretization(
    bin_boundaries=longitude_boundaries,
    name='discretization_longitude')(longitude)

# 将经纬度特征交叉成一个单一的热向量
feature_cross = tf.keras.layers.HashedCrossing(
    # num_bins 可以调整：值越高，精度越高；值越低，性能越高。
    num_bins=len(latitude_boundaries) * len(longitude_boundaries),
    output_mode='one_hot',
    name='cross_latitude_longitude')([latitude, longitude])

# 将我们的输入连接到一个张量中
preprocessing_layers = tf.keras.layers.Concatenate()(
    [feature_cross, median_income, population])

print("Preprocessing layers defined.")


# 定义损失曲线打印函数
def plot_the_loss_curve(epochs, mse_training, mse_validation):
    """打印损失和训练轮次的关系图"""
    plt.figure()
    plt.xlabel("Epoch")
    plt.ylabel("Mean Squared Error")

    plt.plot(epochs, mse_training, label="Training Loss")
    plt.plot(epochs, mse_validation, label="Validation Loss")

    # 由于mse_training是pandas系列，所以需先将其转换为列表
    merged_mse_lists = mse_training.tolist() + mse_validation
    highest_loss = max(merged_mse_lists)
    lowest_loss = min(merged_mse_lists)
    top_of_y_axis = highest_loss * 1.03
    bottom_of_y_axis = lowest_loss * 0.97

    plt.ylim([bottom_of_y_axis, top_of_y_axis])
    plt.legend()
    plt.show()


print("Defined the plot_the_loss_curve function.")


# 定义线性回归模型创建函数
def create_model(my_inputs, my_outputs, my_learning_rate):
    model = tf.keras.Model(inputs=my_inputs, outputs=my_outputs)
    # 将层构造为TensorFlow可以执行的模型
    model.compile(optimizer=tf.keras.optimizers.Adam(
        learning_rate=my_learning_rate),
        loss="mean_squared_error",
        metrics=[tf.keras.metrics.MeanSquaredError()])

    return model


# 创建规范化层以归一化median_house_value数据。
# 因为median_house_value是我们的标签（即我们预测的目标值），所以这些层不会添加到我们的模型中
train_median_house_value_normalized = tf.keras.layers.Normalization(axis=None)
train_median_house_value_normalized.adapt(
    np.array(train_df['median_house_value']))

test_median_house_value_normalized = tf.keras.layers.Normalization(axis=None)
test_median_house_value_normalized.adapt(
    np.array(test_df['median_house_value']))


# 定义模型训练函数
def train_model(model, dataset, epochs, batch_size, label_name, validation_split=0.1):
    """将数据灌入模型以对其进行训练"""
    # 将数据集拆分为特征和标签
    features = {name: np.array(value) for name, value in dataset.items()}
    label = train_median_house_value_normalized(
        np.array(features.pop(label_name)))
    history = model.fit(x=features, y=label, batch_size=batch_size,
                        epochs=epochs, shuffle=True, validation_split=validation_split)

    # 获取有助于绘制损失曲线的详细信息
    epochs = history.epoch
    hist = pd.DataFrame(history.history)
    mse = hist["mean_squared_error"]

    return epochs, mse, history.history


print("Defined the create_model and train_model functions.")


# 定义线性回归模型模型输出
def get_outputs_linear_regression():
    # 创建密集输出层
    dense_output = tf.keras.layers.Dense(units=1, input_shape=(1,),
                                         name='dense_output')(preprocessing_layers)

    # 定义一个输出字典，并发送给模型构造函数
    outputs = {
        'dense_output': dense_output
    }
    return outputs


# 设置超参数
learning_rate = 0.01
epochs = 15
batch_size = 1000
label_name = "median_house_value"

# 将原始训练集拆分为训练集和验证集
validation_split = 0.2

outputs = get_outputs_linear_regression()

# 构建模型拓扑
my_model = create_model(inputs, outputs, learning_rate)

# 基于规范化后的训练集数据训练模型
epochs, mse, history = train_model(my_model, train_df, epochs, batch_size,
                                   label_name, validation_split)
plot_the_loss_curve(epochs, mse, history["val_mean_squared_error"])

test_features = {name: np.array(value) for name, value in test_df.items()}
test_label = test_median_house_value_normalized(test_features.pop(label_name))  # isolate the label
print("\n Evaluate the linear regression model against the test set:")
my_model.evaluate(x=test_features, y=test_label, batch_size=batch_size, return_dict=True)

运行结果如下所示：

 其中，基于测试集（验证集）得到的结果为：loss: 0.3608 - mean_squared_error: 0.3608

5.深度神经网络模型

5.1 定义深度神经网络（DNN）模型

如下代码单元中，get_outputs_dnn 函数定义深度神经网络（DNN）的拓扑，指定以下内容：

  • 深度神经网络中的层数。
  • 每个层中的节点数。

get_outputs_dnn 函数还定义了每一层的激活函数。第一个密集层将我们之前定义的预处理层作为输入。

# 定义深度神经网络模型
def get_outputs_dnn():
    # 创建一个包含20个节点的密集层
    dense_output = tf.keras.layers.Dense(units=20, input_shape=(1,),
                                         activation='relu',
                                         name='hidden_dense_layer_1')(preprocessing_layers)
    # 创建一个具有12个节点的密集层
    dense_output = tf.keras.layers.Dense(units=12, input_shape=(1,),
                                         activation='relu',
                                         name='hidden_dense_layer_2')(dense_output)
    # 创建密集输出层
    dense_output = tf.keras.layers.Dense(units=1, input_shape=(1,),
                                         name='dense_output')(dense_output)

    # 定义一个输出字典，并发送给模型构造函数
    outputs = {
        'dense_output': dense_output
    }

    return outputs

5.2 调用函数来构建和训练深度神经网络

如下代码单元用于训练深层神经网络。我们可以调整三个超参数，看看是否可以减少测试集的损失。

# 设置超参数
learning_rate = 0.01
epochs = 20
batch_size = 1000

# 指定标签
label_name = "median_house_value"

# 将原始训练集拆分为训练集和验证集
validation_split = 0.2

dnn_outputs = get_outputs_dnn()

# 构建模型拓扑
my_model = create_model(
    inputs,
    dnn_outputs,
    learning_rate)

# 在规范化训练集上训练模型。我们通过了整个规范化训练集，但模型将只使用我们输入中定义的特征
epochs, mse, history = train_model(my_model, train_df, epochs,
                                   batch_size, label_name, validation_split)
plot_the_loss_curve(epochs, mse, history["val_mean_squared_error"])

# 根据训练集构建模型后，根据测试集测试该模型
test_features = {name: np.array(value) for name, value in test_df.items()}
test_label = test_median_house_value_normalized(np.array(test_features.pop(label_name)))  # isolate the label
print("\n Evaluate the new model against the test set:")
my_model.evaluate(x=test_features, y=test_label, batch_size=batch_size, return_dict=True)

用 5.2 的代码（训练、测试神经网络模型）替换掉 4.4 节的代码（训练、测试线性回归模型），运行结果如下：

 其中，基于测试集（验证集）得到的结果为：loss: 0.3475 - mean_squared_error: 0.3475。

5.3 优化深度神经网络的拓扑结构

实验，调整深度神经网络的层数和每层中的节点数。旨在实现以下两个目标：

  • 降低测试集的损耗。
  • 最小化深度神经网络中的节点总数。

需要说明的是，上述两个目标可能存在冲突。这里，我们简单尝试一下，如下代码单元所示，

5.3.1 实验一：增加层数

# 定义深度神经网络模型
def get_outputs_dnn():
    # 创建一个包含20个节点的密集层
    dense_output = tf.keras.layers.Dense(units=20, input_shape=(1,),
                                         activation='relu',
                                         name='hidden_dense_layer_1')(preprocessing_layers)
    # 创建一个具有12个节点的密集层
    dense_output = tf.keras.layers.Dense(units=12, input_shape=(1,),
                                         activation='relu',
                                         name='hidden_dense_layer_2')(dense_output)

    # 创建一个具有10个节点的密集层
    dense_output = tf.keras.layers.Dense(units=10, input_shape=(1,),
                                         activation='relu',
                                         name='hidden_dense_layer_3')(dense_output)
    # 创建密集输出层
    dense_output = tf.keras.layers.Dense(units=1, input_shape=(1,),
                                         name='dense_output')(dense_output)

    # 定义一个输出字典，并发送给模型构造函数
    outputs = {
        'dense_output': dense_output
    }

    return outputs

运行结果如下：

其中，基于测试集（验证集）得到的结果为：loss: 0.3451 - mean_squared_error: 0.3451。经过多次实验，我们会发现——增加层数并不能带来损失的有效降低（虽有降低，但并不多），因此，增加层数意义不大，某种意义上，对于这个数据集，两层就是最佳层数。

5.3.2 实验一：减少节点数

模型层数不变（仍采用两层神经网络），我们将节点数量减少 1/2，如下代码单元所示。

# 定义深度神经网络模型
def get_outputs_dnn():
    # 创建一个包含10个节点的密集层
    dense_output = tf.keras.layers.Dense(units=10, input_shape=(1,),
                                         activation='relu',
                                         name='hidden_dense_layer_1')(preprocessing_layers)
    # 创建一个具有6个节点的密集层
    dense_output = tf.keras.layers.Dense(units=6, input_shape=(1,),
                                         activation='relu',
                                         name='hidden_dense_layer_2')(dense_output)

    # 创建密集输出层
    dense_output = tf.keras.layers.Dense(units=1, input_shape=(1,),
                                         name='dense_output')(dense_output)

    # 定义一个输出字典，并发送给模型构造函数
    outputs = {
        'dense_output': dense_output
    }

    return outputs

运行结果如下：

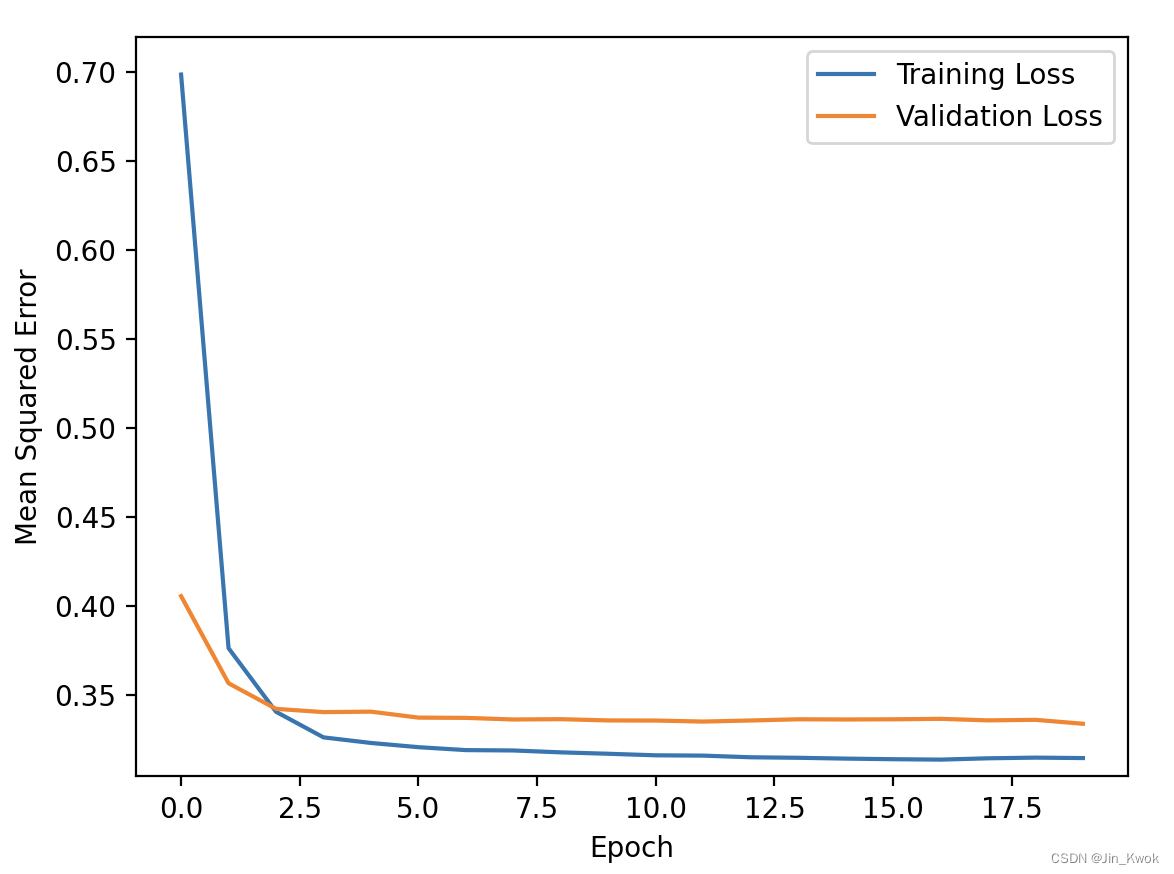
其中，基于测试集（验证集）得到的结果为：loss: 0.3468 - mean_squared_error: 0.3468。相较于原模型（两层，20+12节点），损失有所降低，同时模型节点数量更少，更加简单。事实上，我们可以进一步减少节点数量（两层，6+4节点），也可能取得不错的效果。

神经网络模型，并不是层数越多越好，也不是节点数越多越好，在实践中，我们可通过实验寻找较为合适（预测效果可接受）的层数和节点数，尽量降低复杂度。

6.两种模型结果对比

两种模型在测试集的表现如下所示：

  • 线性回归模型：loss: 0.3608 - mean_squared_error: 0.3608
  • 神经网络模型：loss: 0.3475 - mean_squared_error: 0.3475

假设线性模型收敛，深度神经网络模型也收敛，比较每种模型的测试集损失。在我们的实验中，深度神经网络模型的损失始终低于线性回归模型的损失，这表明深度神经网络模式将比线性回归模型做出更好的预测。

7.参考文献

https://developers.google.cn/machine-learning/crash-course/introduction-to-neural-networks/video-lecture
 

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/726986.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

Dubbo入门详解，API方式与SpringBoot方式

Dubbo入门详解，API方式与SpringBoot方式

Hi I’m Shendi Dubbo入门详解，API方式与SpringBoot方式 在之前一直使用的自己编写的RPC框架，因为是自己编写的，功能上比不过市面上的开源框架，包括后面Spring Cloud系列，如果还用自己编写的话就需要去做整合之类的&am…
阅读更多...
OpenResume一个功能强大的开源简历生成器，太炫了

OpenResume一个功能强大的开源简历生成器，太炫了

OpenResume 是一个功能强大的开源简历生成器和简历解析器。目标是为每个人提供免费的现代专业简历设计，让任何人都能充满信心地申请工作。 核心优势 「实时UI更新」:当输入简历信息时，简历 PDF 会实时更新，因此可以轻松查看最终输出。 「现…
阅读更多...
LeetCode刷题 | 647. 回文子串、516. 最长回文子序列

LeetCode刷题 | 647. 回文子串、516. 最长回文子序列

647. 回文子串 给你一个字符串 s ，请你统计并返回这个字符串中 回文子串 的数目。 回文字符串 是正着读和倒过来读一样的字符串。 子字符串 是字符串中的由连续字符组成的一个序列。 具有不同开始位置或结束位置的子串，即使是由相同的字符组成&#…
阅读更多...
ModaHub魔搭社区：清华开源ChatGLM语言模型一键部署教程

ModaHub魔搭社区：清华开源ChatGLM语言模型一键部署教程

目录 ChatGLM是什么 傻瓜式安装部署 一.下载 二、解压 ChatGLM懒人安装包 ChatGLM是什么 ChatGLM和ChatGPT类似，是由清华大学开发的开源大型语言模型。由于它是开源的，所以带来了很多的可能性，比如可以像Ai绘画一样自己微调模型。 目前…
阅读更多...
老板说，给我把这个 JS React 项目迁移到 TypeScript

老板说，给我把这个 JS React 项目迁移到 TypeScript

在我们日益发展的网络开发领域中，JavaScript 长期以来一直是首选的语言。它的多功能性和普及性推动了许多应用和网站取得成功。然而，随着项目规模和复杂性的增长，维护 JavaScript 代码库可能变得具有挑战性、容易出错且难以扩展。 走出来的第…
阅读更多...
5-Spring cloud之Feign的使用——服务器上实操

5-Spring cloud之Feign的使用——服务器上实操

5-Spring cloud之Feign的使用——服务器上实操 1. 前言2. 搭建Feign2.1 添加子模块——dog-api2.1.1 子模块结构2.1.2 pom文件2.1.3 核心接口DogClientApi 2.2 添加子模块——dog-consumer-feign-802.2.1 子模块结构2.2.2 pom文件2.2.3 yml文件2.2.4 主启动类2.2.5 controller …
阅读更多...
Linux里git的使用

Linux里git的使用

git的使用 一.前置要求1.git的安装2.注册Gitee并创建仓库 二.git三板斧 一.前置要求 1.git的安装 2.注册Gitee并创建仓库 然后记住下面的网址。 之后将仓库克隆到云服务器里。记得输入gitee的账号和密码。 查看目录，可以发现仓库已经在目录里了。 进入目录&#xf…
阅读更多...
python毕设课设大作业《火车票分析助手》程序

python毕设课设大作业《火车票分析助手》程序

在PyCharm中运行《火车票分析助手》即可进入如图1所示的系统主界面。 图1 系统主界面 具体的操作步骤如下： （1）在主界面“车票查询”选项卡中依次输入，出发地、目的地以及出发时间，然后单击“查询”按钮，…
阅读更多...
十九、Jenkins版本构建完成，触发自动化测试

十九、Jenkins版本构建完成，触发自动化测试

十九、Jenkins版本构建完成，触发自动化测试 1.构建后操作-Build other projects 2.关联自动化测试工程 这样版本构建完成，就会执行自动化测试
阅读更多...
金九银十跳槽涨薪Java面试题！568页真题+答案解析，大厂都在考

金九银十跳槽涨薪Java面试题！568页真题+答案解析，大厂都在考

2023年一半又过去了，各大企业的招聘也又开始大量放岗了，各位苟着的小伙伴们要抓住机会了！ 但很多小伙伴对面试不够了解，不知道如何准备，对面试环节的设置以及目的不了解，尤其是面试题还很难，有些…
阅读更多...
RocketMQ5.0--事务消息

RocketMQ5.0--事务消息

RocketMQ5.0–事务消息 一、事务消息概览 RocketMQ事务消息的实现原理基于两阶段提交和定时事务状态回查来决定消息最终是提交还是回滚，消费者可以消费事务提交的消息，如下图所示。事务消息的作用：确保本地业务与消息在一个事务内&#xff0…
阅读更多...
成功解决：java file outside of source root

成功解决：java file outside of source root

前言 我复制一个很小项目的代码，然后重新命名后。用IDEA打开，发现.java文件的左下方有个橘色的标志。 1、问题文件 这里显示 Java file outside of source root。 查阅资料发现：这个问题是指Java文件不在源代码根目录之内。这可能会导致…
阅读更多...
使用pytest命令行实现环境切换

使用pytest命令行实现环境切换

目录 前言 pytest_addoption(parser, pluginmanager) 在conftest.py文件中定义命令行参数 获取命令行参数 设置不同环境的全局变量 定义测试类及测试方法 测试验证 前言 在自动化测试过程中经常需要在不同的环境下进行测试验证，所以写自动化测试代码时需要考…
阅读更多...
Android12之IBinder中[[clang::lto_visibility_public]]作用(一百六十)

Android12之IBinder中[[clang::lto_visibility_public]]作用(一百六十)

简介： CSDN博客专家，专注Android/Linux系统，分享多mic语音方案、音视频、编解码等技术，与大家一起成长！ 优质专栏：Audio工程师进阶系列【原创干货持续更新中……】🚀 人生格言： 人生…
阅读更多...
MySQL自治平台建设的内核原理及实践（上）

MySQL自治平台建设的内核原理及实践（上）

总第565篇 2023年 第017篇 本文整理自美团技术沙龙第75期的主题分享《美团数据库攻防演练建设实践》，系超大规模数据库集群保稳系列（内含4个议题的PPT及视频）的第4篇文章。 本文作者在演讲后根据同学们的反馈，补充了很多技术细节&…
阅读更多...
如何绘制「UML类图」

如何绘制「UML类图」

一、UML类图简介 类图以反映类的结构(属性、操作)以及类之间的关系为主要目的，描述了软件系统的结构，是一种静态建模方法。类图用来描述系统中有意义的概念，包括具体的概念、抽象的概念、实现方面的概念等，是对现实世界中事物的抽…
阅读更多...
设计模式--------结构型模式

设计模式--------结构型模式

结构型模式 结构型模式描述如何将类或对象按某种布局组成更大的结构。它分为类结构型模式和对象结构型模式，前者采用继承机制来组织接口和类，后者釆用组合或聚合来组合对象。 由于组合关系或聚合关系比继承关系耦合度低，满足“合成复用原则”…
阅读更多...
web 页面布局：（三）position 坐标系布局

web 页面布局：（三）position 坐标系布局

web 页面布局：（三）position 坐标系布局 页面坐标系position 设置fixedrelativeabsolutesticky 应用场景 页面坐标系 因为所有文本内容，是从左向右读，自上而下读，和书写习惯，读书习惯一致&#…
阅读更多...
惊呆了！这个银行管理技巧也太厉害了吧

惊呆了！这个银行管理技巧也太厉害了吧

在金融行业，蓄电池监控是一项至关重要的任务。随着金融机构的数字化转型和依赖电力的增加，蓄电池成为保障金融系统正常运行的关键组成部分。 因此，对蓄电池的状态进行监控和维护，确保其高效可靠地工作，对金融行业的稳定…
阅读更多...
深度学习06-pytorch从入门到精通

深度学习06-pytorch从入门到精通

文章目录 概述环境准备安装cuda和cudnn安装pytorch 基础张量定义numpy转换数学函数随机数计算函数矩阵处理函数 自动梯度案例计算图 torchvision模块TransformsDataSetDataLoader自定义数据集 nn模块nn.ModuleCNN图像处理层nn.Conv2dnn.AvgPool2d和nn.MaxPool2dnn.Linearnn.Bat…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023