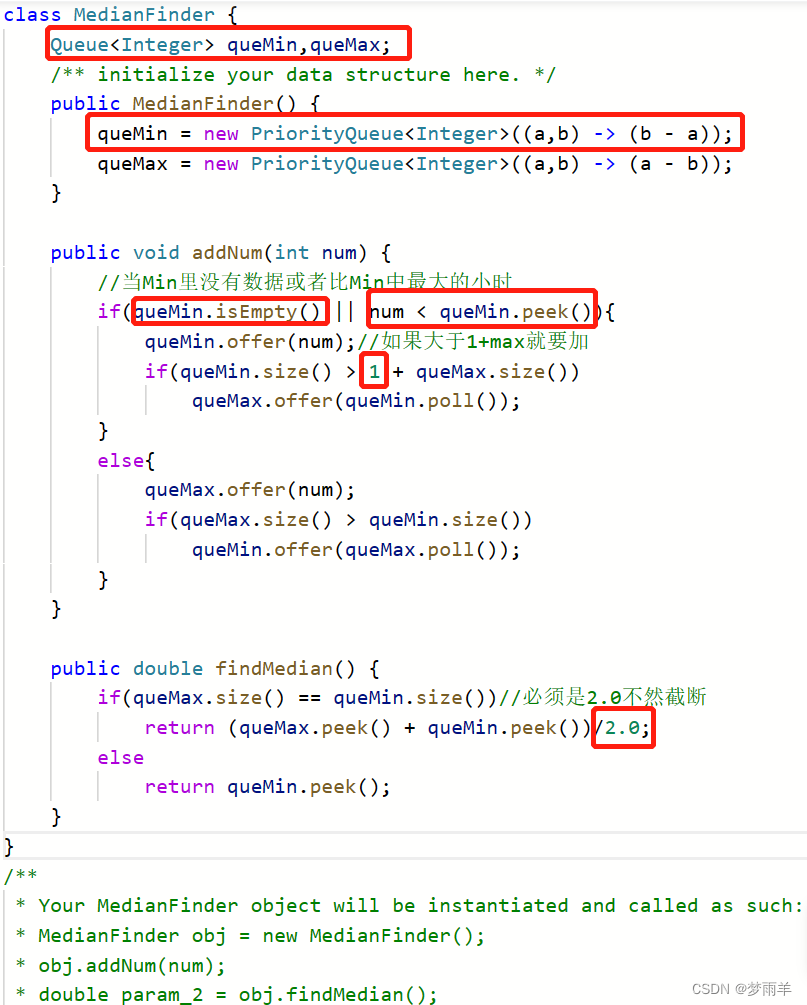
这道题用的优先队列非常好，一边维护一个左半边，一边维护一个右半边。（注意：较大的一半不用改变规则，因为出都是默认出小的）。然后每次和小的队列开头的数比较（即偏小那个队列的最大值）。加完之后由于会排序，所以最大/小的又会分别和冒泡一样冒出来。

时间复杂度：

addNum\textit{addNum}addNum: O(log⁡n)O(\log n)O(logn)，其中 nnn 为累计添加的数的数量。
findMedian\textit{findMedian}findMedian: O(1)O(1)O(1)。
空间复杂度：O(n)O(n)O(n)，主要为优先队列的开销。

首先，因为是三个函数都要使用的队列，所以声明要写在函数外，类体的开头。还有个要注意的，由于两个队列存的值都是int类型，所以除出来的结果也是整数，最后才会转为double，所以得除2.0！不然结果会截断。还有最好用offer()和poll()而不是add()和remove()！！