系列文章目录

---

---

前言

用链表来实现二叉树。

---

一、链式二叉树的定义

每个节点用结构体来表示，其中有每个节点都有指向左右孩子节点的指针，如果没有孩子则为NULL。

二、链式二叉树的实现

typedef  int BTDataType;

typedef struct BinaryTreeNode
{
	BTDataType data;
	struct BinaryTreeNode* left;
	struct BinaryTreeNode* right;
}BTNode;

三、链式二叉树的遍历

链式二叉树的增删查改没有价值。
搜索二叉树的增删查改有价值。
搜索二叉树又可以引申出平衡搜索树（AVL树+红黑树）

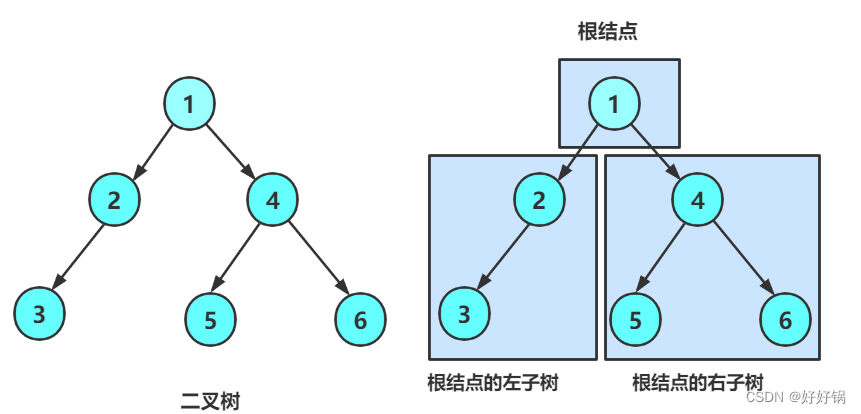
任何一个树都可以分出三部分：根节点、左子树、右子树。
空树不能再分了：NULL。

管理思维/分治思想：一个节点的遍历 = 左孩子节点的遍历 + 右孩子节点的遍历 + 该节点
所以每个节点都要遍历，左右孩子节点的遍历组成父节点的遍历，如果是空节点则遍历就是NULL
遍历一个节点就是遍历这个节点为根的树

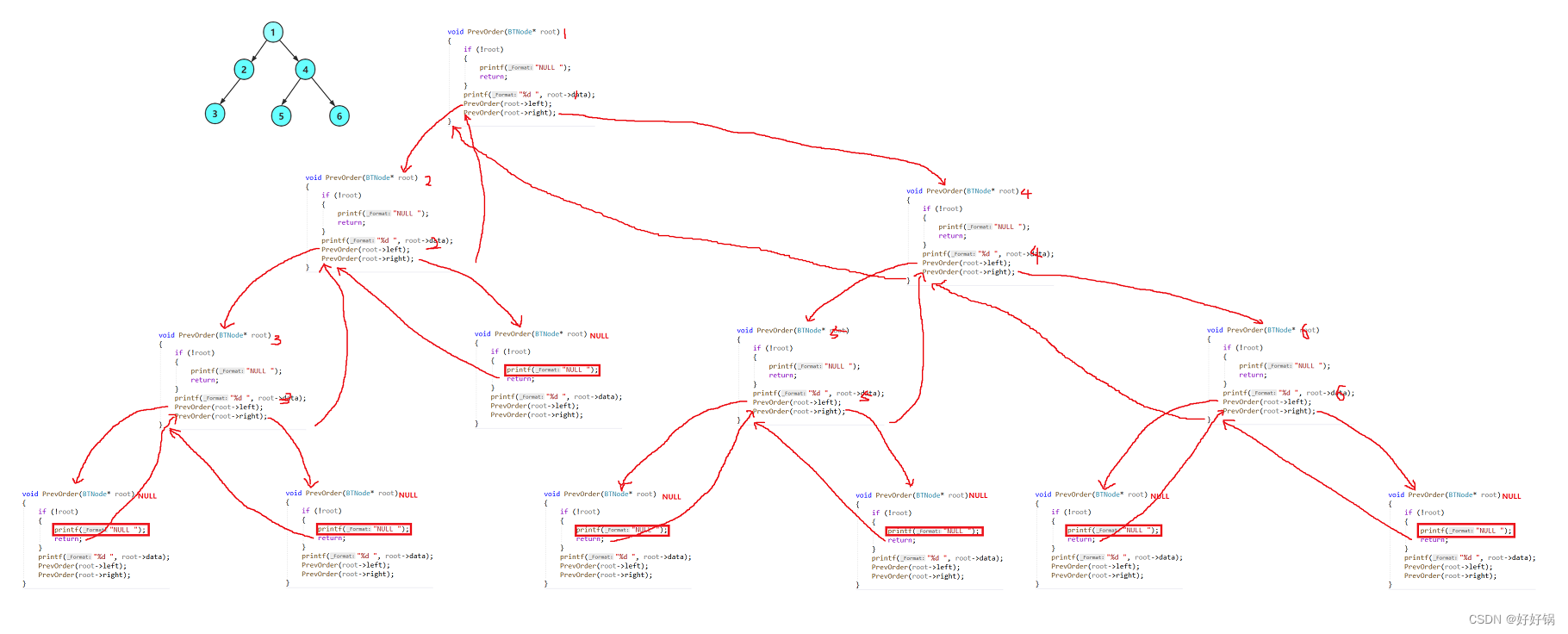
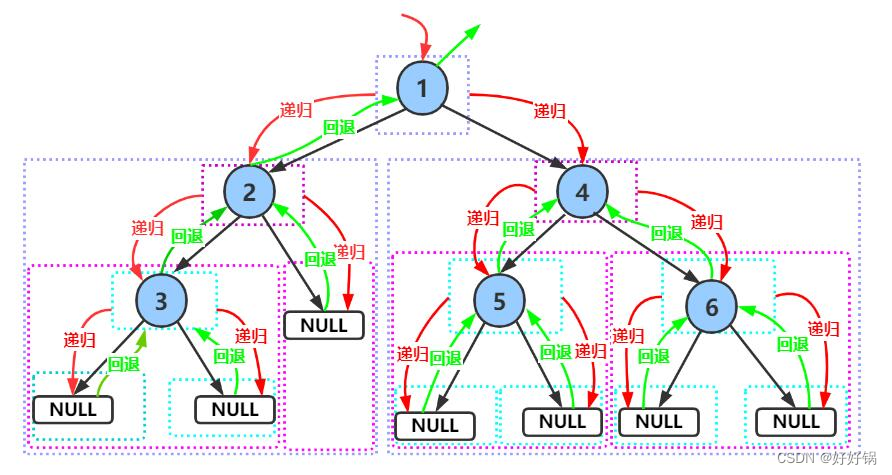
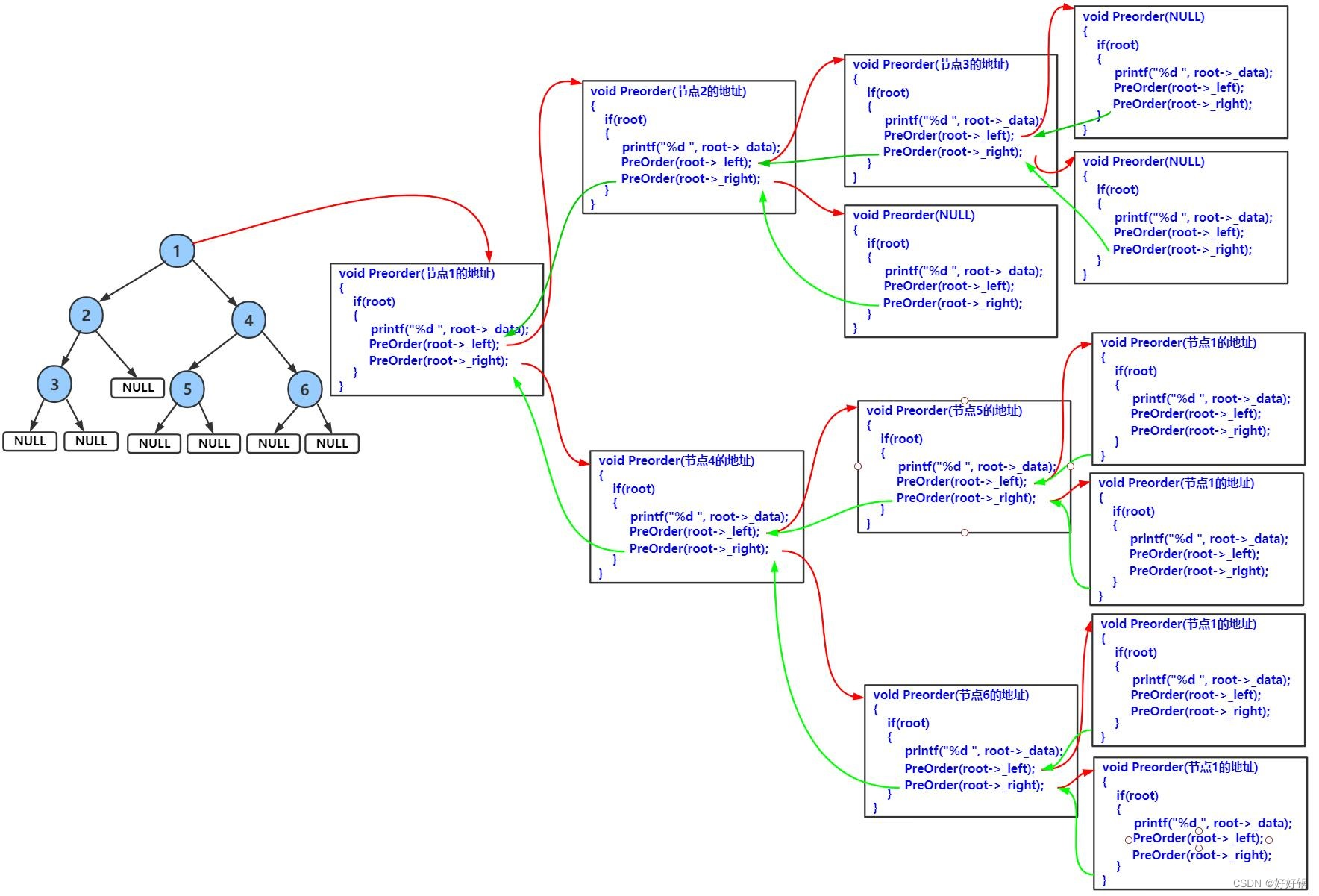
1、前序遍历/先根遍历

遍历顺序：根、左子树、右子树

void PrevOrder(BTNode* root)
{
	if (!root)
	{
		printf("NULL ");
		return;
	}
	printf("%d ", root->data);
	PrevOrder(root->left);
	PrevOrder(root->right);
}

2、中序遍历/中根遍历

遍历顺序：左子树、根、右子树

void InOrder(BTNode* root)
{
	
	if (!root)
	{
		printf("NULL ");
		return;
	}
	InOrder(root->left);
	printf("%d ", root->data);
	InOrder(root->right);
}

3、后序遍历/后根遍历

遍历顺序：左子树、右子树、根

void PostOrder(BTNode* root)
{
	if (!root)
	{
		printf("NULL ");
		return;
	}
	PostOrder(root->left);
	PostOrder(root->right);
	printf("%d ", root->data);
}

4、层序遍历

遍历顺序：一层一层走
运用队列：出一层，带下一层

void LevelOrder(BTNode* root)
{
	Queue q;
	QueueInit(&q);
	if (root) QueuePush(&q, root);
	while (!QueueEmpty(&q))
	{
		BTNode* front = QueueFront(&q);
		printf("%d ", front->data);
		//队列出上一层，带下一层
		QueuePop(&q);

		if (front->left)
		{
			QueuePush(&q, front->left);
		}

		if (front->right)
		{
			QueuePush(&q, front->right);
		}
	}
	QueueDestory(&q);
}

5、前/中/后序遍历的关系

前序/后序：确定根
中序：确定左右子树

四、节点个数以及高度等

1. 二叉树节点的个数

int TreeSize(BTNode* root)
{
	if (!root)
	{
		return 0;
	}
	return TreeSize(root->left) + TreeSize(root->right) + 1;
}

2. 二叉树叶子节点个数

int TreeLeafSize(BTNode* root)
{
	if (!root) return 0;
	if (root->left || root->right)
	{
		return TreeLeafSize(root->left) + TreeLeafSize(root->right);
	}
	else
	{
		return 1;
	}
}

3. 求树的高度/深度

int TreeHeight(BTNode* root)
{
	if (!root) return 0;
	
	int leftHeight = TreeHeight(root->left);
	int rightHeight = TreeHeight(root->right);

	return leftHeight > rightHeight ? leftHeight + 1 : rightHeight + 1;
}

4. 求第k层的节点个数

int TreeKlevelSize(BTNode* root, int k)
{
	if (!root) return 0;

	if (k == 1) return 1;

	if (k > 1) return TreeKlevelSize(root->left, k-1) 
		+ TreeKlevelSize(root->right, k-1);
}

5. 二叉树查找值为x的节点

BTNode* TreeFind(BTNode* root, BTDataType x)
{
	if (!root) return NULL;

	if (root->data == x) return root;
	
	BTNode* leftnode = TreeFind(root->left, x);
	if (leftnode) return leftnode;

	BTNode* rightnode = TreeFind(root->right, x);
	if (rightnode) return rightnode;	
	
	return NULL;
}

五、 二叉树的创建和销毁

1. 通过前序遍历的数组"ABD##E#H##CF##G##"构建二叉树

BTNode* rebuildTree(char* str, int* pi) {
    if (str[*pi] == '#') {
        (*pi)++;
        return NULL;
    }
    BTNode* root = (BTNode*)malloc(sizeof(BTNode));
    root->val = str[(*pi)++];

    root->left = rebuildTree(str, pi);
    root->right = rebuildTree(str, pi);
    return root;
}

2. 二叉树销毁

void TreeDestory(BTNode* root)
{
	if (root == NULL)
	{
		return;
	}

	TreeDestory(root->left);
	TreeDestory(root->right);
	free(root);
}

3. 判断二叉树是否是完全二叉树

bool TreeComplete(BTNode* root)
{
	Queue q;
	QueueInit(&q);
	if (root)
		QueuePush(&q, root);

	while (!QueueEmpty(&q))
	{
		BTNode* front = QueueFront(&q);
		QueuePop(&q);

		if (front == NULL)//遇到空就可以开始判断
		{
			break;
		}
		else
		{
			QueuePush(&q, front->left);
			QueuePush(&q, front->right);
		}

	}

	while (!QueueEmpty(&q))
	{//出现空后，如果后面全是空的话就是完全二叉树
		BTNode* front = QueueFront(&q);
		QueuePop(&q);
		if (front != NULL)
		{
			QueueDestory(&q);
			return false;
		}
	}
	QueueDestory(&q);
	return true;
}

总结

链式二叉树是用链表来实现二叉树，用递归来遍历二叉树。
水激石则鸣，人激志则宏。——秋瑾