一、向量

我们确定一个坐标系，也就是一个线性空间的基 (e1, e2, e3)， 那就可以谈论向量 a 在这组基下的坐标了：

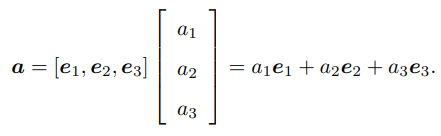
 1.1 内积

内积可以描述向量间的投影关系

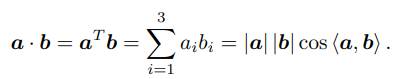
 1.2 外积

外积的方向垂直于这两个向量，大小为 |a| |b|sin 〈a, b〉，是两个向量张成的四边形的 有向面积。

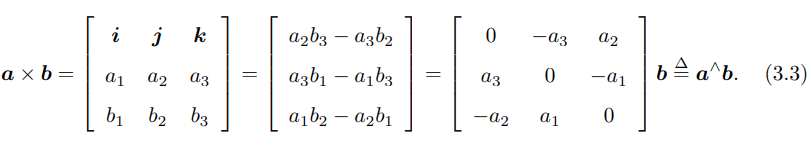
 对于外积，我们引入了 ∧ 符号，把 a 写成一个矩阵。事实上是一个反对称矩阵 （Skew-symmetric），你可以将 ∧ 记成一个反对称符号。这样就把外积 a × b，写成了矩阵 与向量的乘法 a ∧b，把它变成了线性运算。