【Talk】VALSE 20200415 | 机器学习 vs 压缩感知:核磁共振成像与重建
文章目录
- 【Talk】VALSE 20200415 | 机器学习 vs 压缩感知:核磁共振成像与重建
- Deep learning for MR imaging and analysis - Shanshan Wang
- Machine Learning for CS MRI: From Model-Based Methods to Deep Learning - Bihan Wen
- 重建问题简介
- 压缩感知介绍
- Model-based method: Transform learning for better sparsity
- 基本概念
- 1.Transform learning Method 1: Sparsifying Transform Learning(STL)
- 2.Unitary Transform Learning (UT)
- 3. Learning a UNIon of Transforms (UNITE)
- 4.Flipping and Rotation Invariant Sparsifying Transform (FRIST)
- 5. Sparsifying TRansfOrm Learning and Low-Rankness (STROLLR)
- 总结
- 讨论
- Deep Learning
- 一些主流模型
- 深度学习模型和传统模型的对比
报告主页:http://valser.org/article-359-1.html
20200415 机器学习 vs 压缩感知:核磁共振成像与重建
PPT:Shanshan Wang slides | Bihan Wen slides
谷歌学术:
- 王珊珊 Shanshan Wang | siat
- 文碧汉 | ntu
Deep learning for MR imaging and analysis - Shanshan Wang
可以参考前面链接中的ppt,这里不重点讲,我们主要关注文碧汉老师的talk。
Machine Learning for CS MRI: From Model-Based Methods to Deep Learning - Bihan Wen
重建问题简介
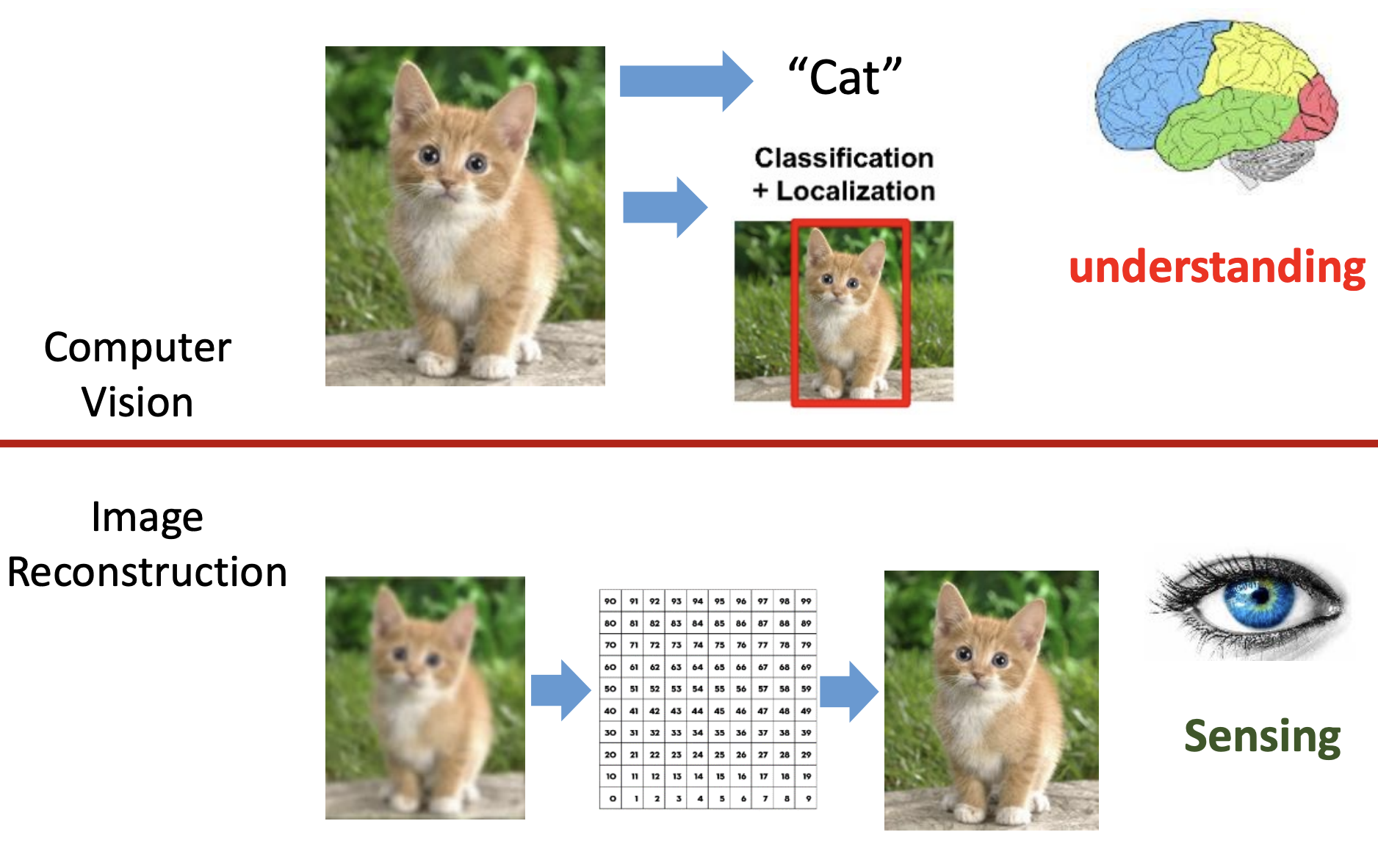
计算机视觉准确来说是图像理解,成像/重建的本质是感知,从低质量观测恢复高质量图像。
MRI成像过程可以看做下面的公式:
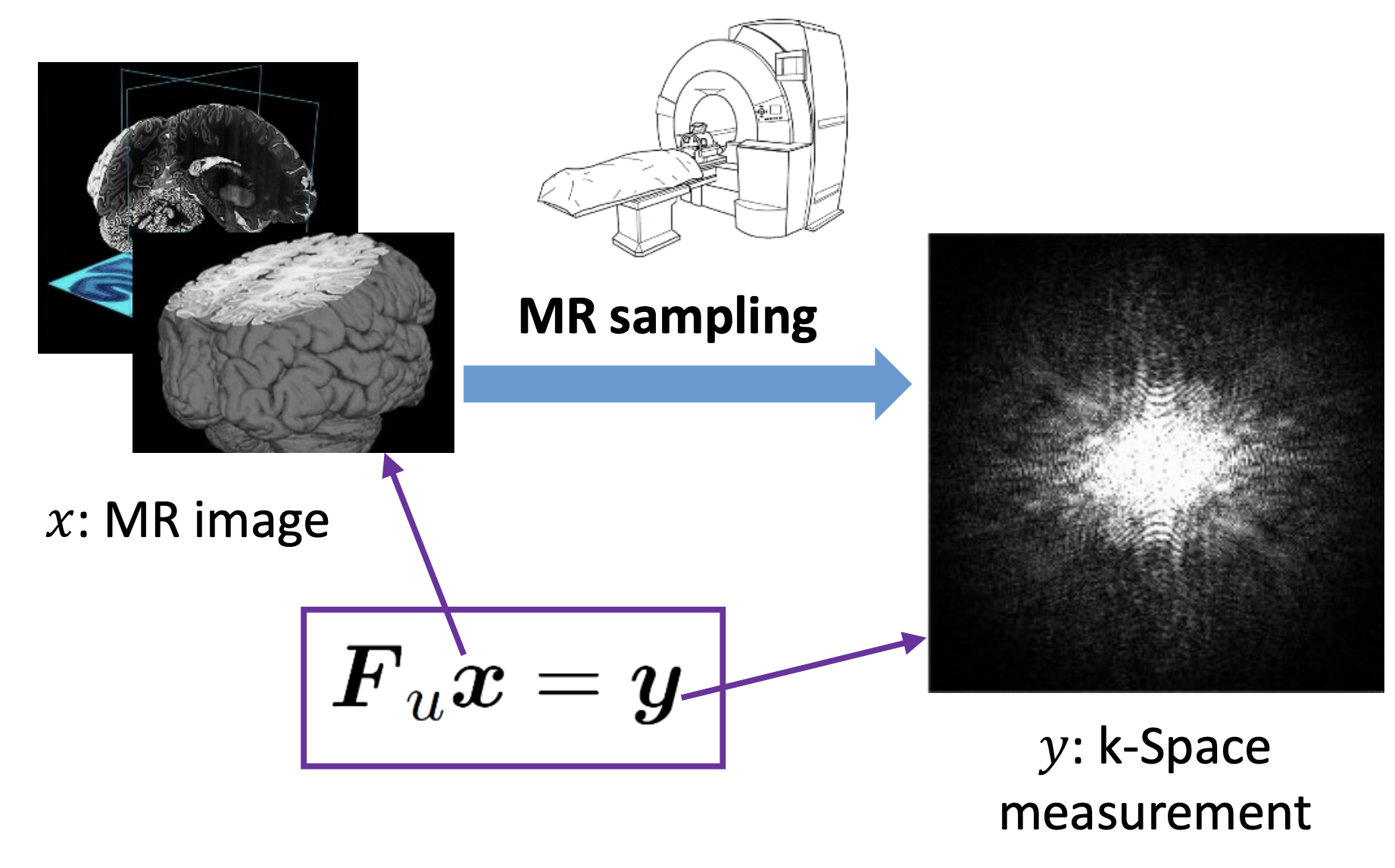
理想情况下k-space是连续的,但是由于信息的采集都是的数字信号,因此采集到的都是离散化的数据,因此可以说采集到的k-空间的全采样图像都是真实情况下的欠采样。
但是我们要讨论的情况是在全采样情况下的欠采样,也就是对全采样的图像我们只采样部分区域,如下图:
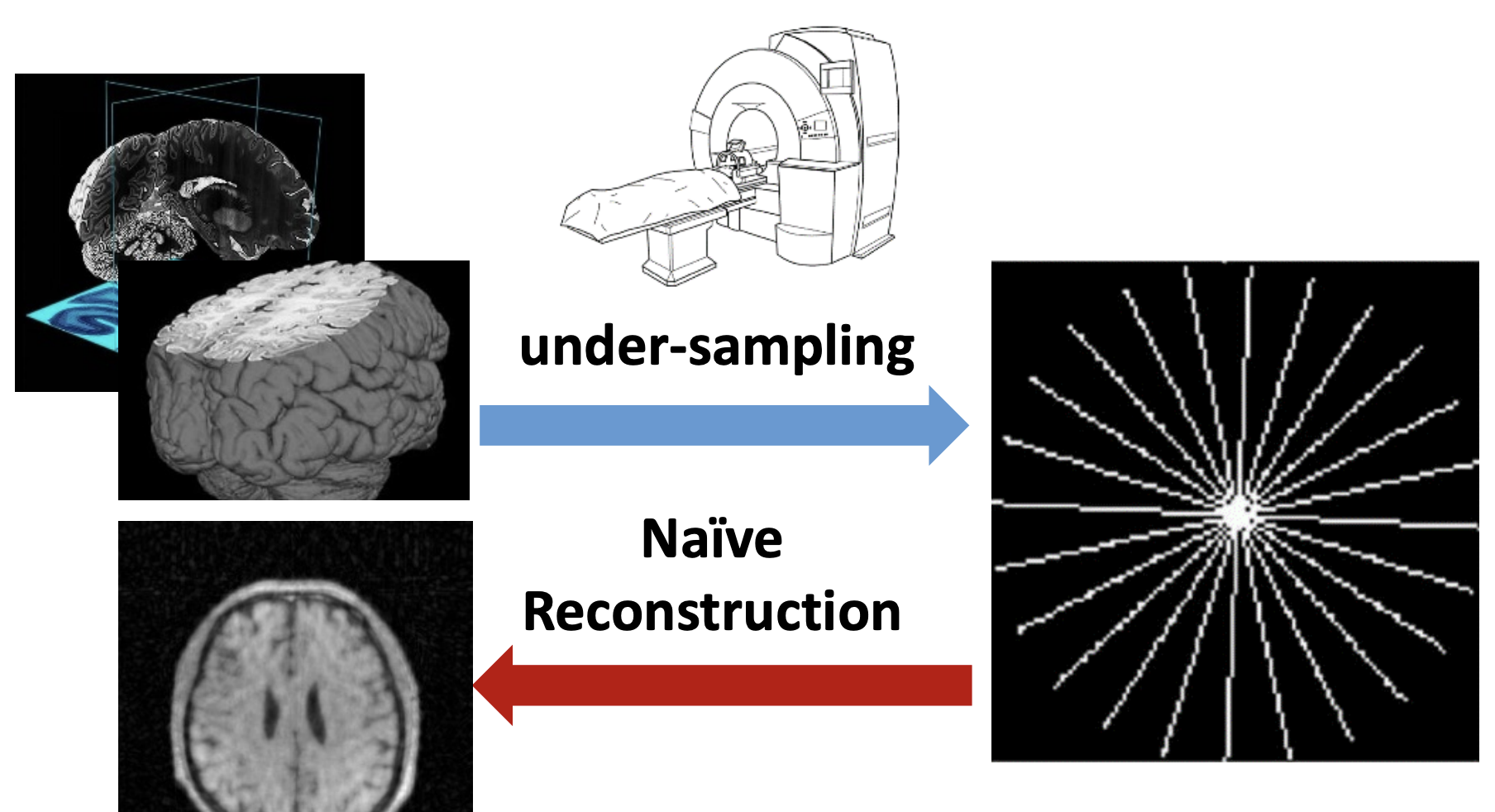
但是直接求解这个逆过程是一个ill-posed 问题。在十年前,压缩感知作为一个比较好的方法在重建领域大放异彩。
压缩感知介绍
经典压缩感知公式如下
-
有约束优化问题(Transform domain sparsity):利用MR成像的关系式 F u x = y F_ux=y Fux=y,我们设计一个有约束的优化问题。目标在固定的Transform(变换)下的最优的sparsity,找到使得sparsity最优的 x x x。
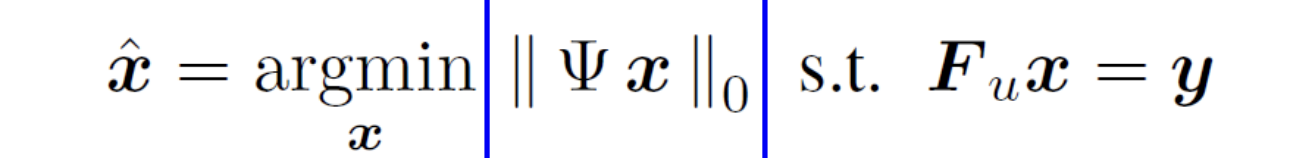
-
无约束优化问题:sparsity作为正则项
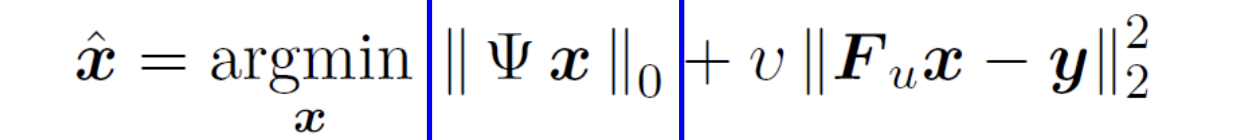
稀疏性
①为什么sparsity比较重要?
image model的作用如下,即提供判断是否为我们想要的图像的依据。
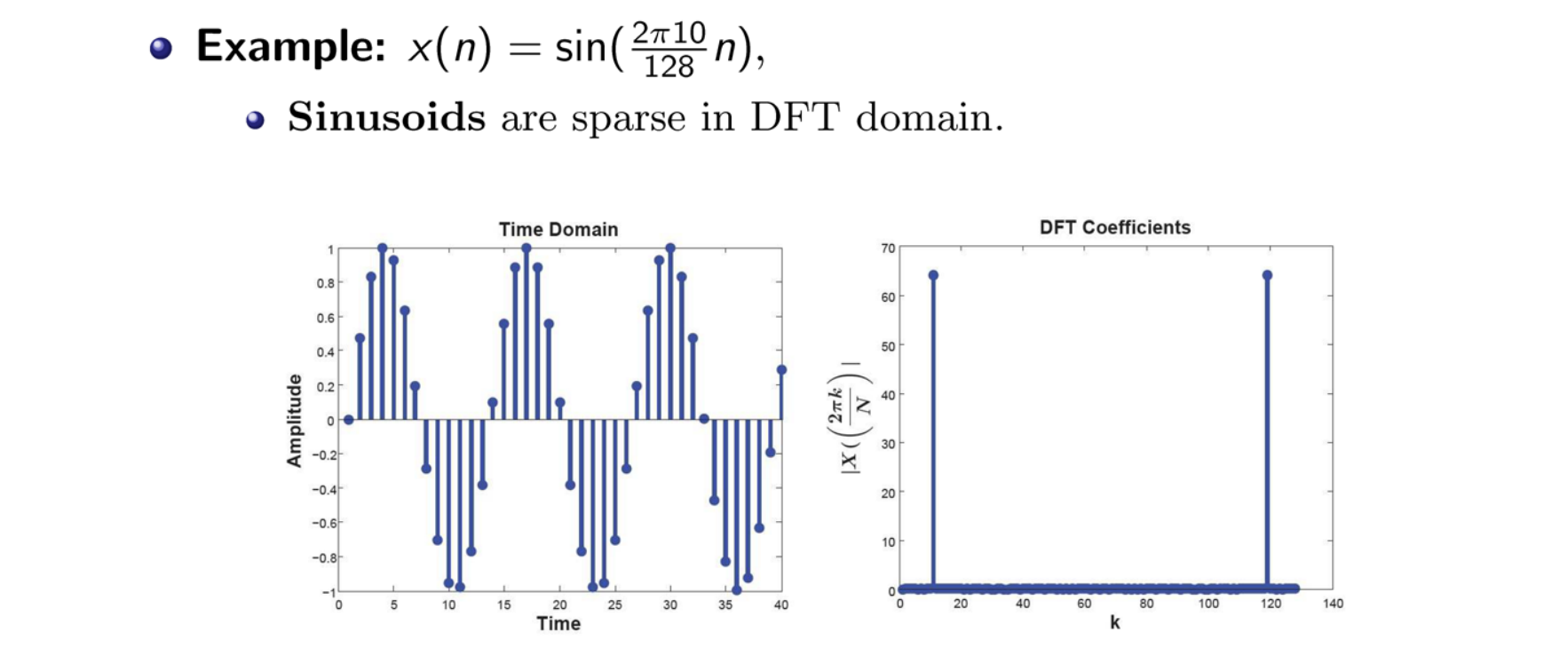
②信号的稀疏性定义
定义:一个dense的信号在transform domain是稀疏的
举例:一个一维信号是稀疏的 ⇔ \Leftrightarrow ⇔大多数相关系数为0
特点:自然信号大都是满足sparsity属性的,例如自然图像的离散余弦变换
而噪声的离散余弦变换仍为噪声:
磁共振重建领域的压缩感知方法发展如下:
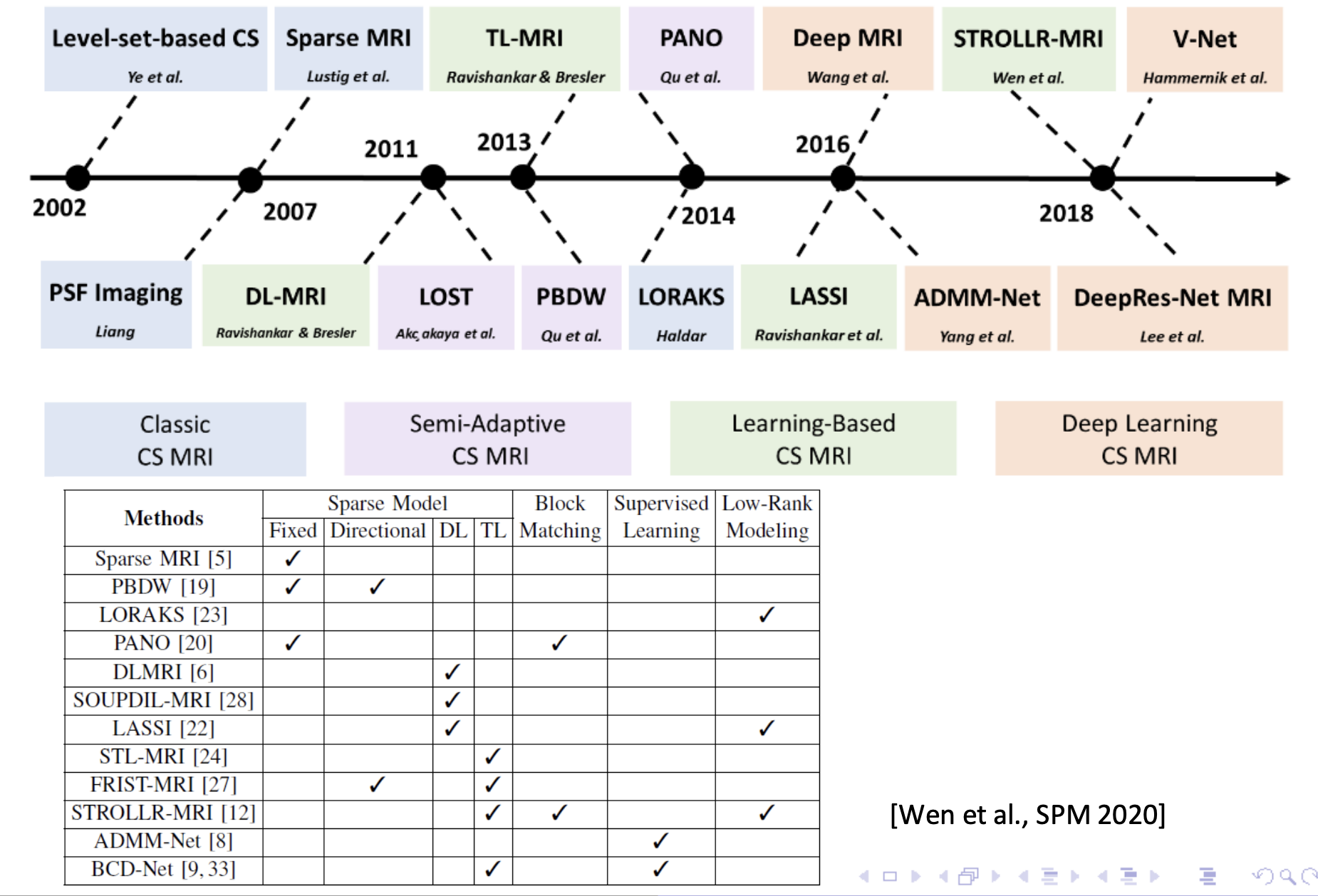
Model-based method: Transform learning for better sparsity
基本概念
在压缩感知中,我们给定了一个变换 Ψ \Psi Ψ(如DCT、小波等等),求得这个变换下最稀疏的 x x x。如下式:

但是我们希望去学习这个变换,使得稀疏化更好,如下图:
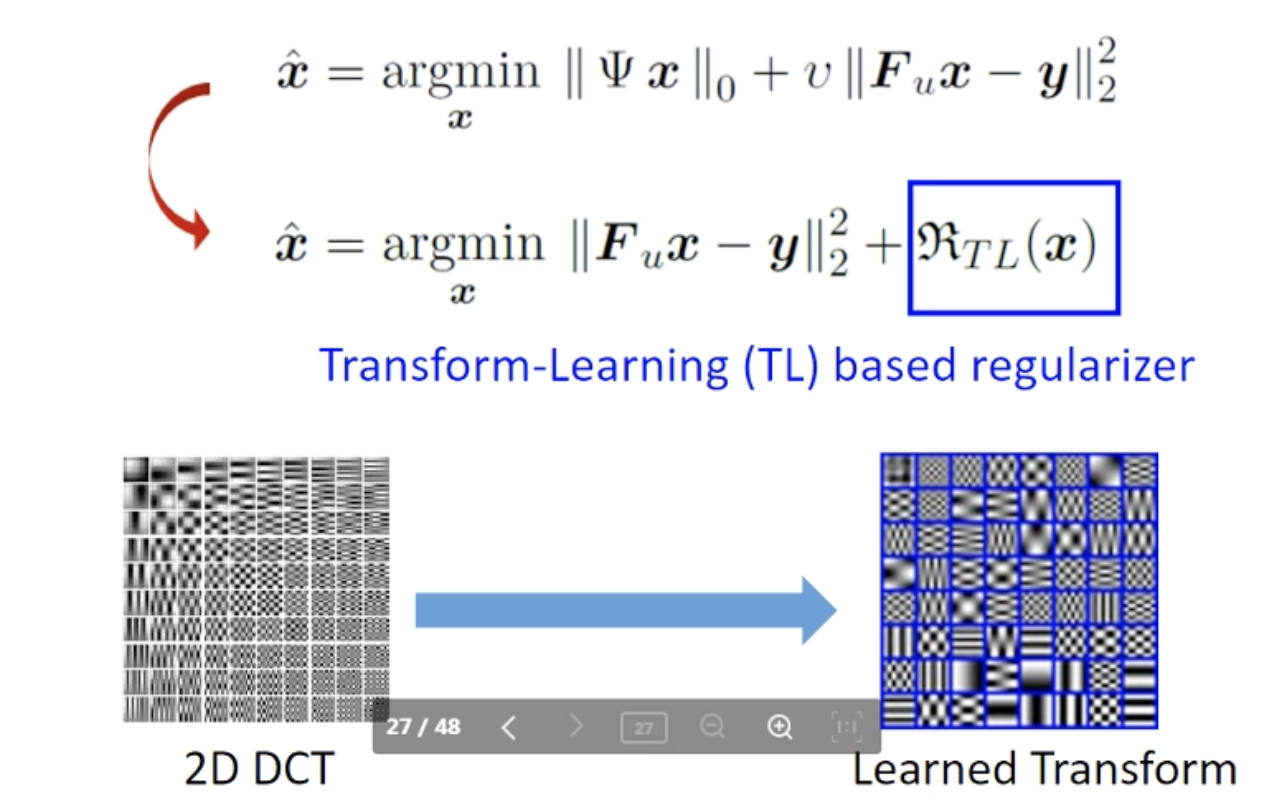
1.Transform learning Method 1: Sparsifying Transform Learning(STL)
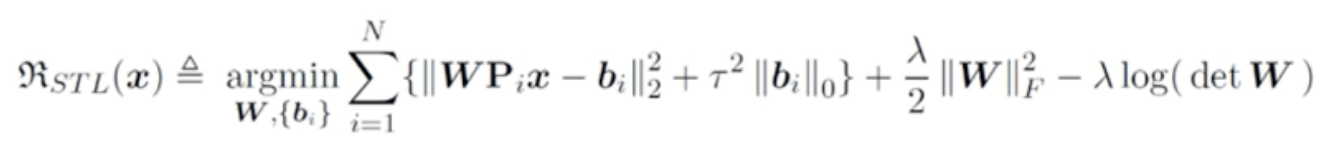
符号解释:
W \mathbf{W} W: 要学习的变换矩阵; b i \mathbf{b}_i bi: patch对应的sparse code
P i \mathbf{P}_i Pi: 图像中的第 i i i个patch;
λ 2 ∥ W ∥ F 2 − λ l o g ( d e t W ) \frac \lambda 2 \Vert \mathbf W\Vert^2_F - \lambda log(det \mathbf W) 2λ∥W∥F2−λlog(detW): 保证了 W , b \mathbf W,\mathbf b W,b不会变成一个trivial的解:为0,保证让 λ 2 ∥ W ∥ F 2 \frac \lambda 2 \Vert \mathbf W\Vert^2_F 2λ∥W∥F2其尽量趋近于1
该方法的优缺点:
① 有闭式解
2.Unitary Transform Learning (UT)

算法的具体实现过程: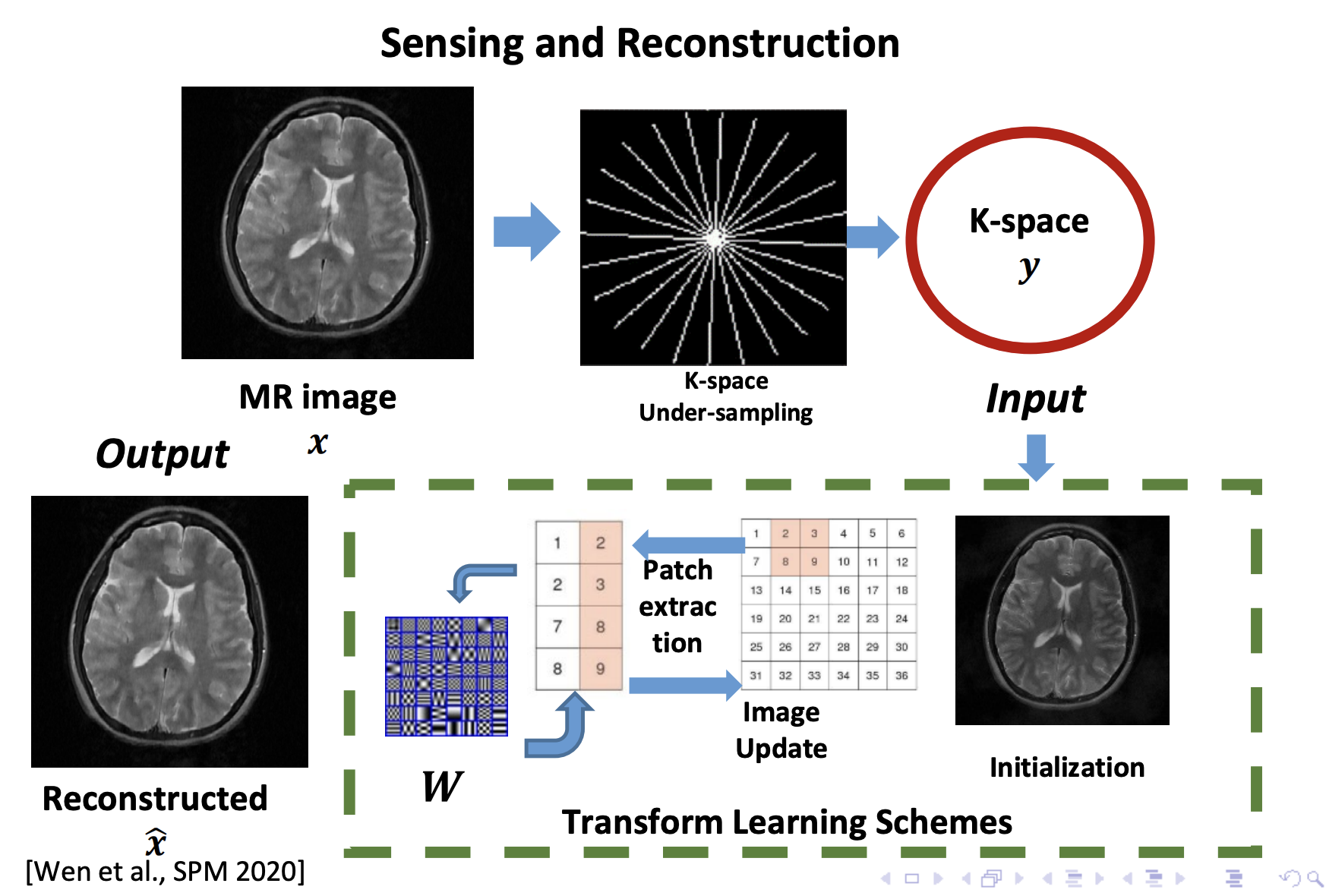
3. Learning a UNIon of Transforms (UNITE)

图像比较复杂的情况下,一个transformer是不够的。
4.Flipping and Rotation Invariant Sparsifying Transform (FRIST)

5. Sparsifying TRansfOrm Learning and Low-Rankness (STROLLR)
有的时候不光使用sparsity,也可以构建Low-rank,将二者结合在一起约束。

总结
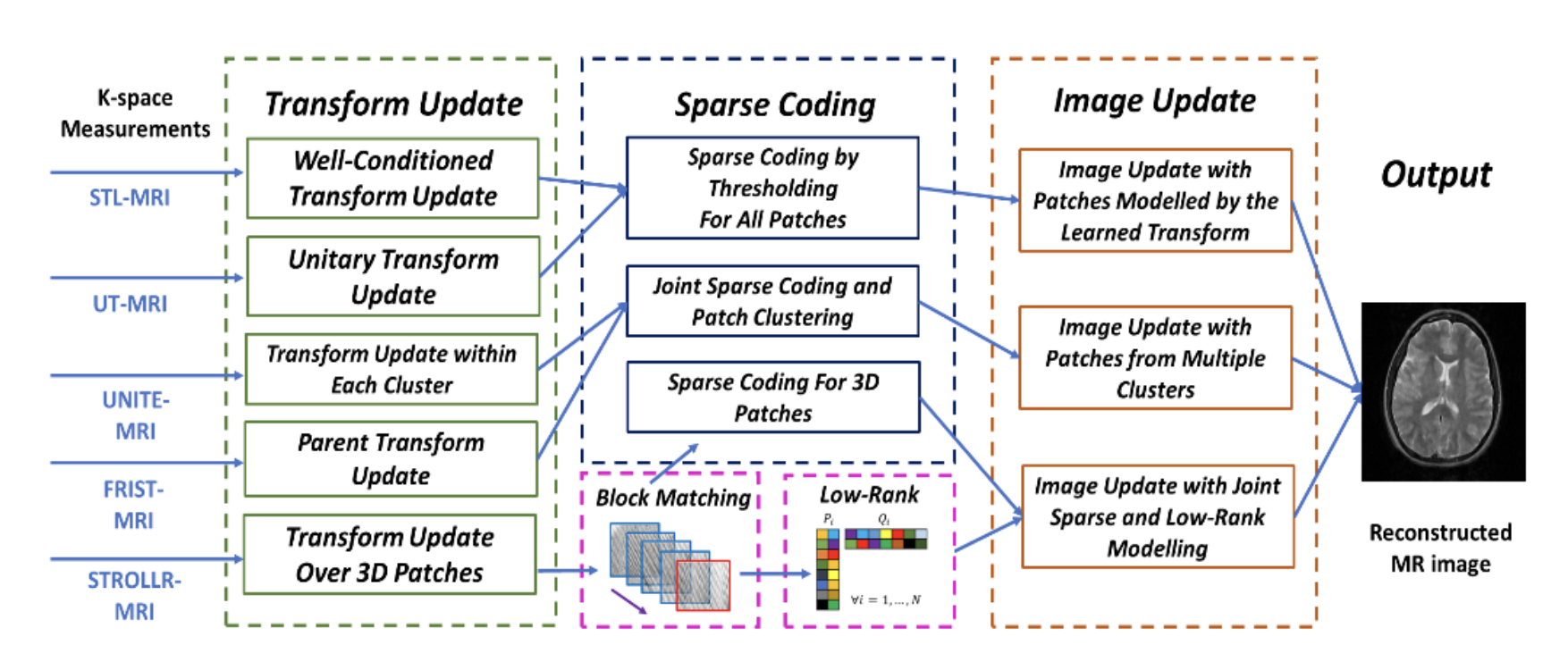
讨论
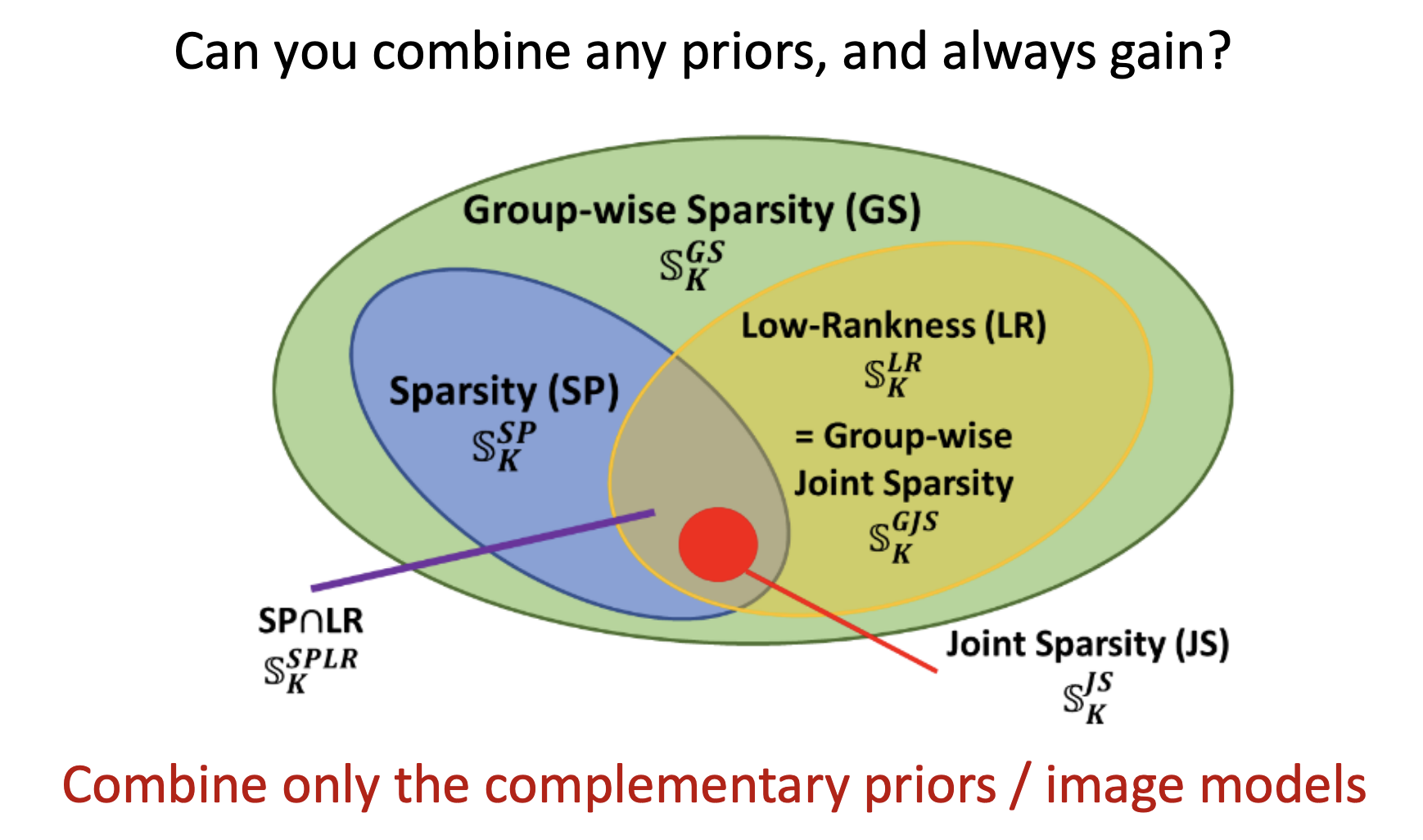
注:不同的model在不同的MRI中有不同的效果,需要选择更适合的方法,达到最好的效果。
Deep Learning
一些主流模型
model的发展,即model灵活性的上升,模型具有更好的适应性: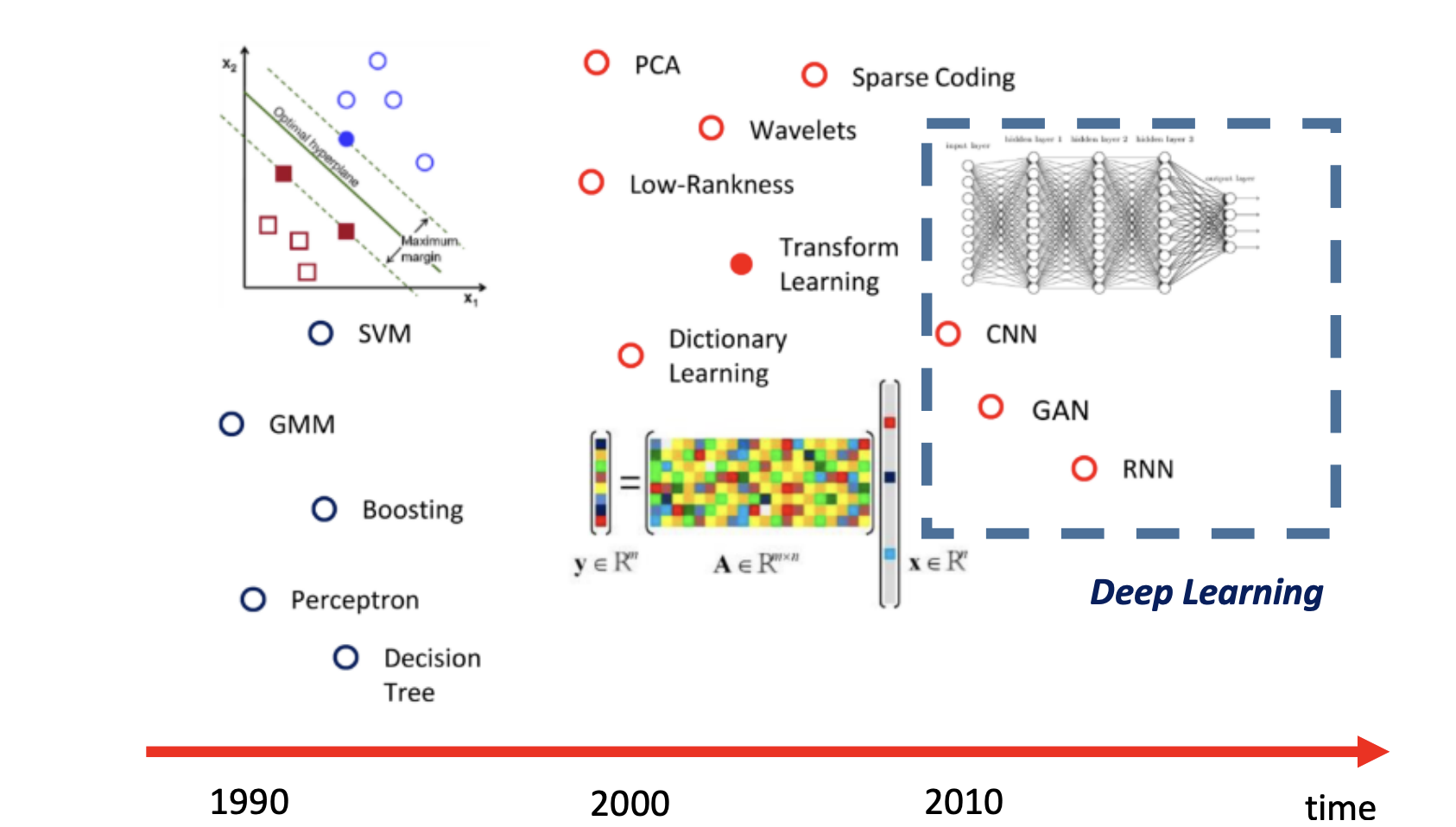
下面我们主要关注两种方向:①unroll network(主流),将迭代过程变为多个network,如下图:
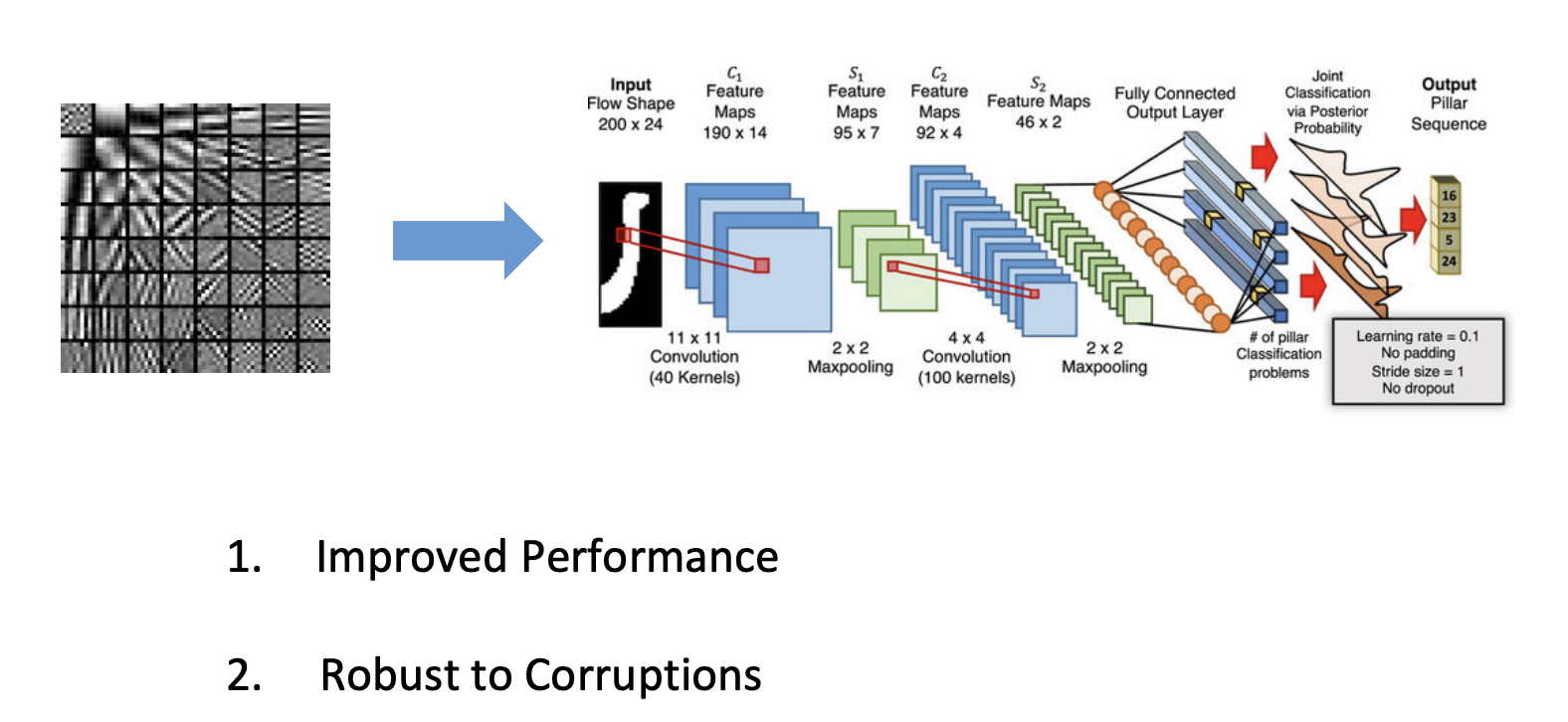
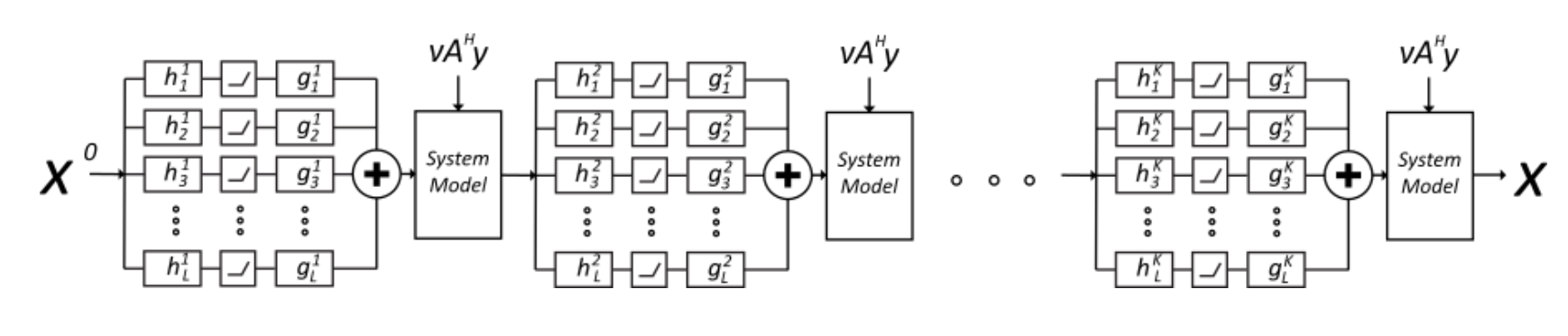
②另一种想法就是设计多层的transform:
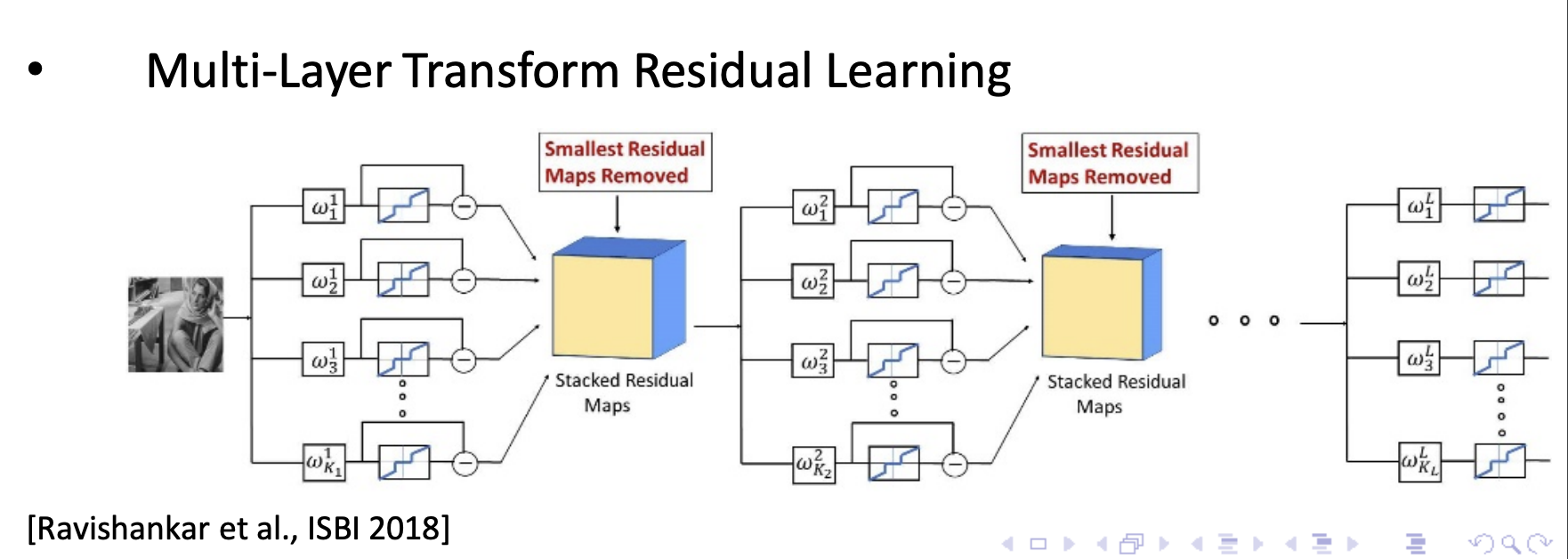
一些结果:
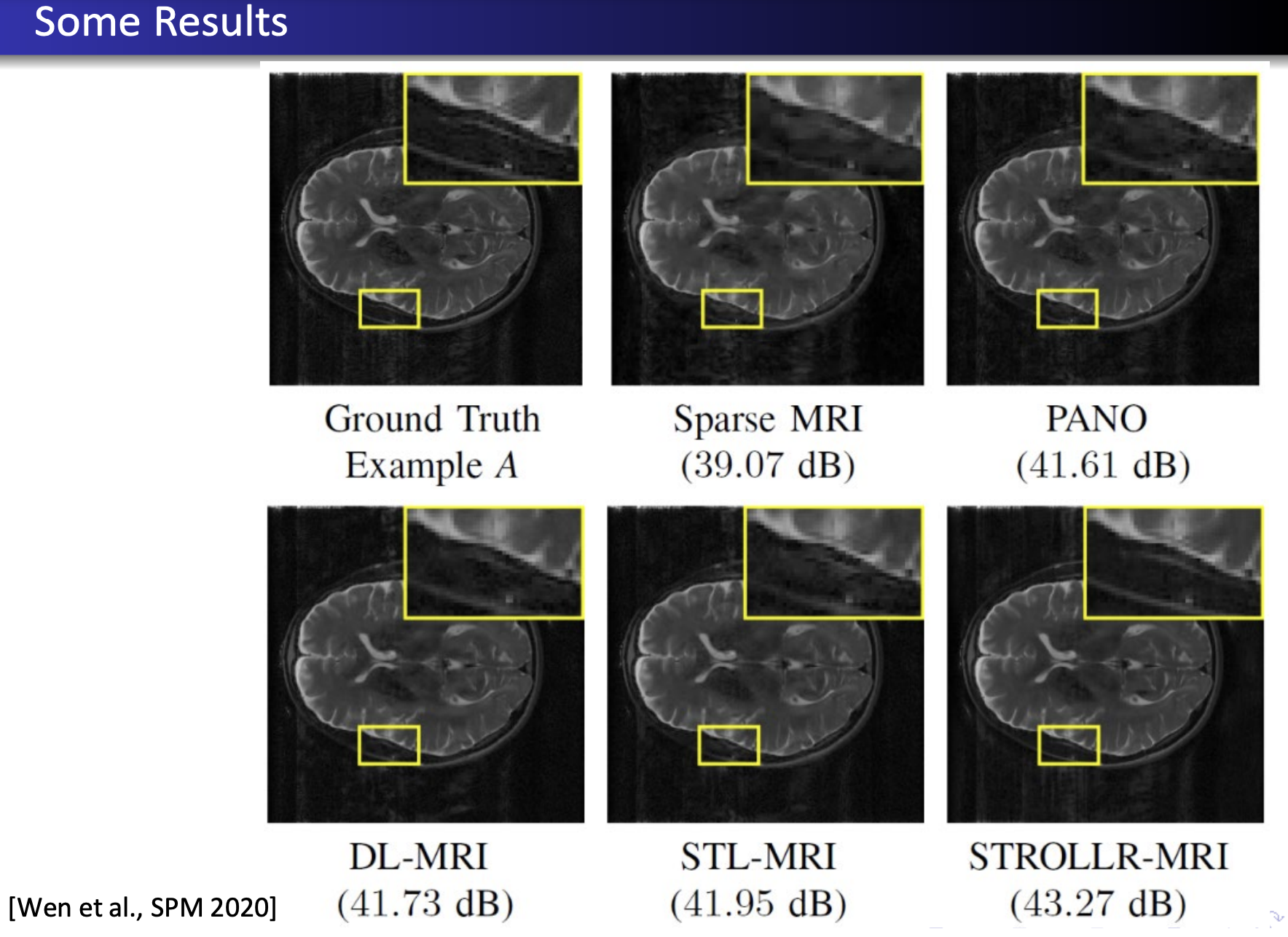
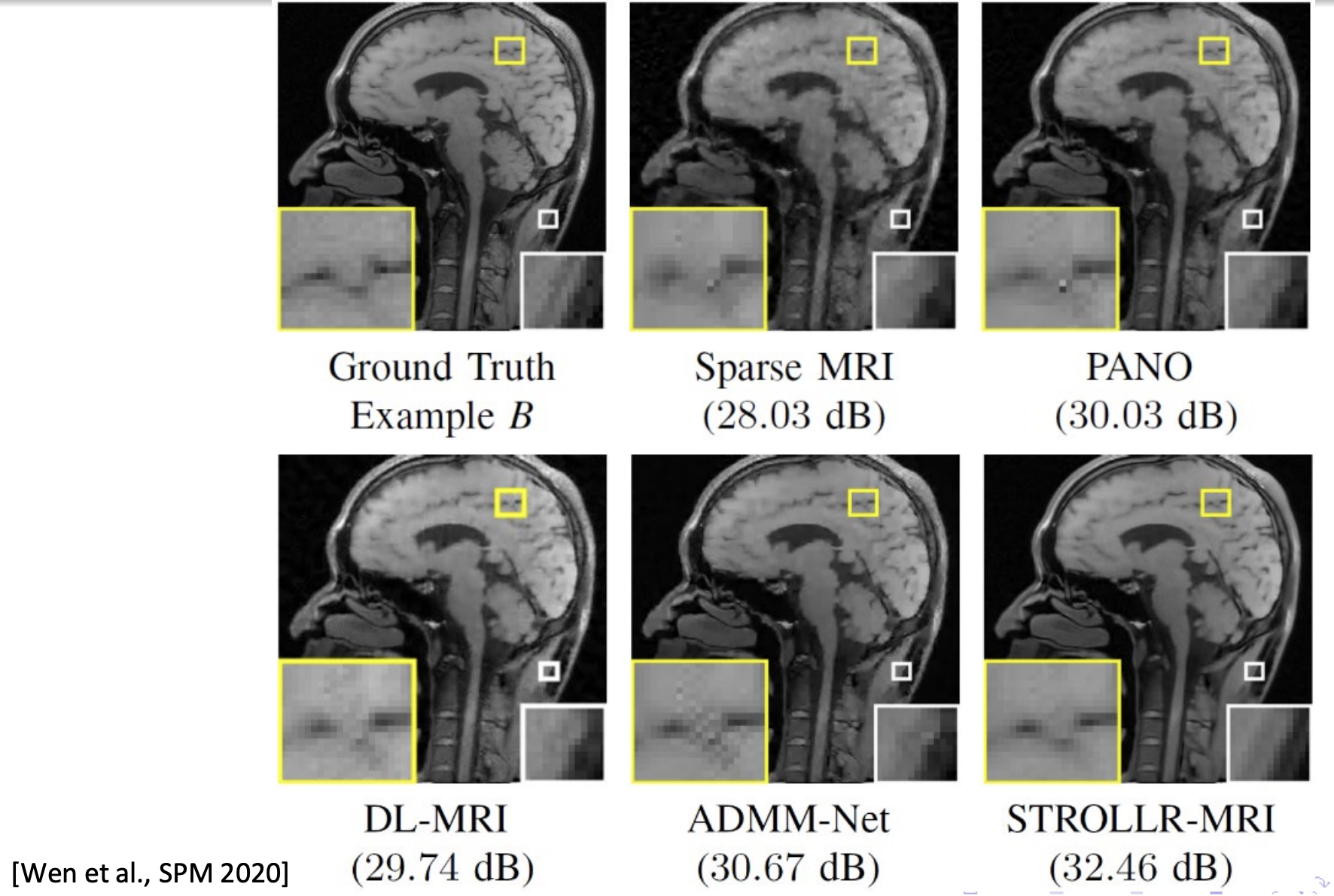
此外,自监督的方式也有一定的优势:我们希望模型不只是拘泥于数据集,而要一定程度上focus在图像本身,根据图像本身的一些全局和局部信息进行重建。
深度学习模型和传统模型的对比




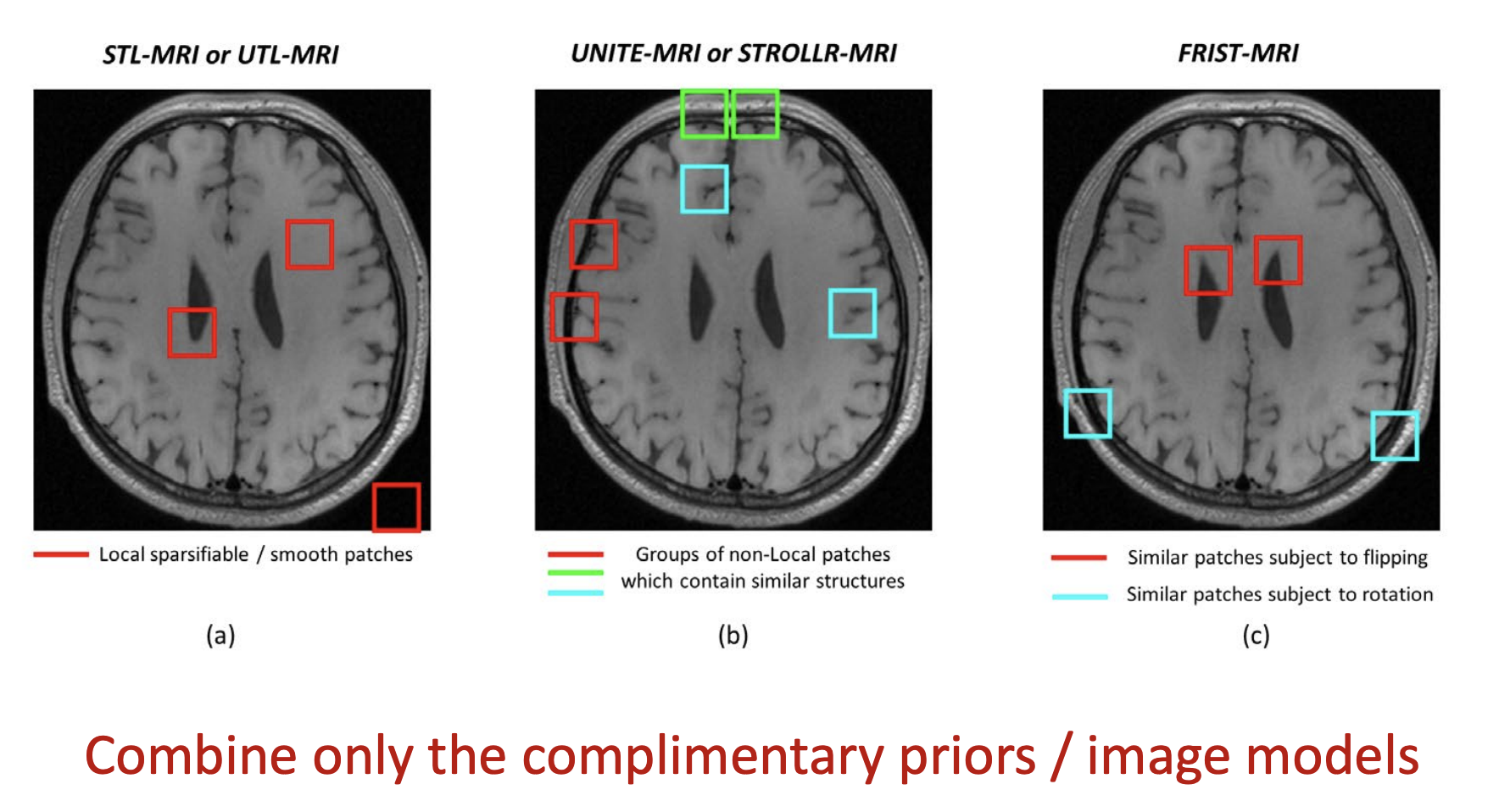








![[PG]生成表注释SQL](https://img-blog.csdnimg.cn/a72ad5d8da2948968e43328361c4a33a.png)