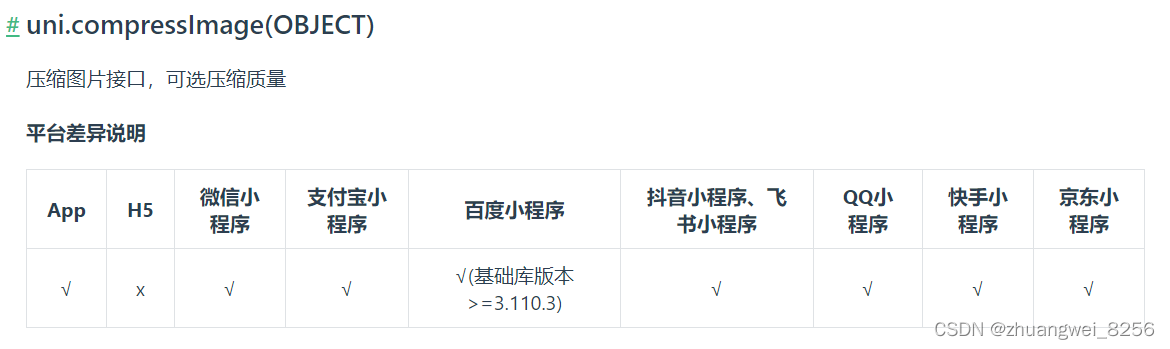
问题描述

  现有n种不同形状的宝石，每种宝石有足够多颗。欲将这些宝石排列成m行n列的一个矩阵，m≤n，使矩阵中每行和每列的宝石都没有相同的形状。试设计一个算法，计算出对于给定的m和n，有多少种不同的宝石排列方案。

数据输入

  由文件input.txt给出输入数据。第1行有2个正整数m和n(0<m≤n<9)。

运行结果

  共有n种形状的宝石，排成m行n列，每一行和每一列的宝石都没有相同的形状，即每行都有n种宝石，只需将n种宝石全排列，判断每一列是否有相同形状的宝石即可。
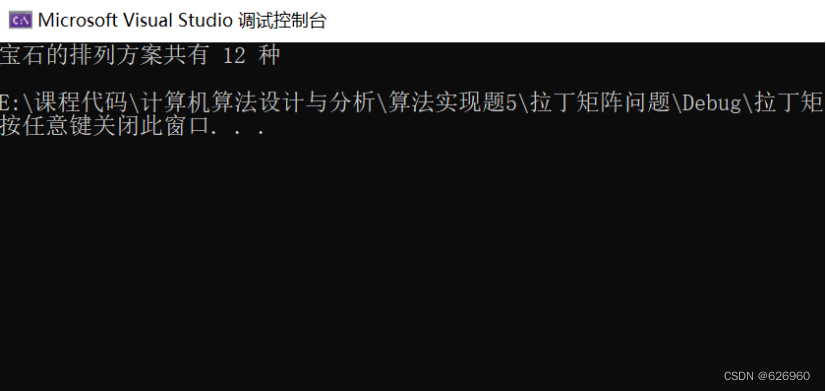
  设n和m都为3，编写代码，运行程序，得到的排列方案数为12。

代码

#include<stdio.h>
#define n 3
#define m 3

int a[m][n];
int count = 0;

//判断数组的每行每列是否有重复的数，如果有，返回false；否则，返回true
bool ok(int x, int y) 
{
	for (int i = 0; i < x; i++)
		if (a[i][y] == a[x][y])
			return false;
	for (int j = 0; j < y; j++)
		if (a[x][j] == a[x][y])
			return false;
	return true;
}
//进行回溯
void traceback(int x, int y) 
{
	int temp;
	//排列并判断，在每行每列没有重复的情况下
	for (int i = y; i < n; i++) 
	{
		temp = a[x][y];
		a[x][y] = a[x][i];
		a[x][i] = temp;
		if (ok(x, y)) {
			if ((x == m - 1) && (y == n - 1))   //如果走到最后一层，输出
			{
				count++;
			}
			else if ((x == m - 1) && (y != n - 1))   //如果走到最后一行但不是最后一列，列加一
				traceback(x, y + 1);
			else if ((x != m - 1) && (y == n - 1))   //如果走到最后一列但不是最后一行，行加一,列变成第一列
				traceback(x + 1, 0);
			else        //否则，继续回溯,列加一
				traceback(x, y + 1);
		}
		temp = a[x][y];
		a[x][y] = a[x][i];
		a[x][i] = temp;
	}
}
int main()
{
	//给数组进行赋值
	for (int i = 0; i < m; i++) 
	{
		for (int j = 0; j < n; j++)
			a[i][j] = j + 1;
	}
	traceback(0, 0);
	printf("宝石的排列方案共有 %d 种\n", count);
	return 0;
}