Numpy学习(参考)

一、前言

二、numpy官方文档

文档划分

参数规范

一、前言

对于numpy学习，我相信没有一篇绝对完整的学习资料。当然通过多年摸索和实战经验的人肯定有更多的numpy知识储备并且具备一定的numpy知识结构总结能力。

所以这里提前说一下，不要抱着通过一两篇或多篇文章就能学明白numpy的心理。numpy官方文档后面对相关知识的整理并不是很好，所以如果要学好numpy更多的是实践应用和回顾复习（我也期待有大神能分享富具结构性和完整性的numpy学习文档）。

在该篇文章，我会给出个人关于numpy官方文档的部分学习经验内容，然后也会给出numpy基本操作的相关内容。

二、numpy官方文档

文档划分

官方文档总共划为以下几部分：
一、Array objects：
   译为“数组对象”块。然后这块又分了以下几个小块(我会说明每个小块的内容)：
   (1) numpy.ndarray：所谓ndarray即N-dimensional array，表示n维数组的意思。然后为什么说这是一个必要性学习的类？因为我们创建出来的numpy数组都是该实例(即numpy.ndarray类型)，所以该类中定义的方法和属性都是可以用于我们创建后的数组实例，然后在这块刚好文档比较全的都列出了，我们可以常看一下明知一下(如果你有时间甚至可以做一个归类)。
   (2) Scalars：译为“标量”块，主要主要介绍了标量的各种类型以及他们的继承关系别名，然后还介绍了numpy.generic类的一些属性和方法。
   (3) dtype object：译为“数据类型”块，上面“Scalars”块是已经讲了数据类型的，这里的数据类型主要指的是数据类型对象(即numpy.dtype实例)，然后这块主要介绍numpy.dtype的一些属性和方法。
   (4) Indexing routines：译为“索引常用”块，这里主要介绍了和索引用法相关的一些数组操作方法。
   (5) Iterating Over Arrays：译为“遍历数组”块，是的“Iterating Over”就是“遍历”的意思。当然这块主要介绍一些不同的方式去遍历数组来进行一些数组操作。
   (6) Standard array subclasses：译为“标准数组子类”块，主要介绍了numpy.ndarray类的相关数组子类如numpy.matrix、numpy.charray等等。
   (7) Masked arrays：译为“掩码数组”块，主要介绍了numpy.ma模块的一些方法和类来创建并操作掩码数组。
   (8) The array interface protocol：译为“数组接口协议”块。
   (9) Datetimes and TimeDeltas：译为“日期时间和时间差”块，主要介绍日期时间类型和时间差的相关操作。


二、Array API Standard Compatibility：
   译为“数组API标准兼容性”块，主要介绍版本的一些变动。

三、Constants：
   译为“常量”块，主要介绍了numpy模块中定义的一些常量

四、Universal functions(ufunc)：
   译为“全体方法”块，为什么叫全体方法块呢？因为是对数组进行逐元素操作(涉及元素遍历)，这里官方文档给出了名词具体解释。在这块主要学习一个类numpy.ufunc，这里会介绍其相关的一些方法属性。

五、Routines：
   译为“常用”块，这块就是我们主要学习的块，介绍了数组常用的一些操作，这里面的内容是比较多的。

六、Typing(numpy.typing)：
   译为“类型”块
七、Global State：
   译为“全局状态”块

八、Numpy C-API：
九、CPU/SIMD Optimizations：
十、Numpy security：
十一、Numppy and SWIG：

学习路线：Routines >> Universal functions >> Array objects >> 其他
后面会更新补全，没提到的块内容，已经被弃用不用再看了。

参数规范

        这里就是说一下numpy方法的一些规范特点，有助于我们更快速理解记忆和使用那些方法。因为很多方法的参数都有一样的参数缩写，我们明确缩写规范含义就能很快知道怎么使用这些方法了。

        a：表示array-like，类数组的意思，类数组并不要求一定是数组，只要序列的嵌套规范符合数组格式那么就可以称为是一个类数组
        arr/array：表示array，这个就明确要求一定是数组对象了
        axis：指定的一个轴，是一个整数值，一般默认为None(常将数组扁平化处理)
        axes：也是轴，不同的是是一个轴序列，一般用于多轴之间的操作

Routines学习(部分)

1、创建

### 前言：
    文档在这块第一部分介绍了数组的创建，对于数组的创建文档中是做了归类的，是比较合理的。一共分为以下几类：From shape or value(从形状或值特性)、From existing data(从已存在的数据)、Creating record arrays(记录数组)、Creating character arrays(字符数组)、Numerical ranges(根据数值范围)、Building matrices(构建矩阵)、The Matrix class(矩阵类)。
    当然官方文档都已经总结了，所以这里只做引入和补充，不做赘余。
    对应的学习链接：https://numpy.org/doc/stable/reference/routines.array-creation.html#the-matrix-class。


### record arrays(记录数组)：
    Record arrays（记录数组）是 NumPy 中的一种特殊数据结构，用于存储异构数据（具有不同数据类型的数据）的结构化数组。
    在 NumPy 中，通常情况下，数组的所有元素必须具有相同的数据类型。然而，有时我们需要处理具有不同数据类型的数据集，例如表示表格、数据库记录或结构化数据的情况。这时，可以使用记录数组来处理这种异构数据。
    以下为示例：
    import numpy as np
    # 定义数据类型和字段名称
    dt = np.dtype([('name', 'S20'), ('age', 'i4'), ('height', 'f4')])
    # 创建记录数组
    arr = np.array([('Alice', 25, 165.5), ('Bob', 30, 180.2)], dtype=dt)
    

### *_like方法
    比如说numpy.full和numpy.full_like，功能都是一样的，用于根据指定值来填充从而创建一个新数组。
    其实这个like指的是array-like，也就是*_like方法与对应名称的方法不同的是，*_like方法要给一个数组即array-like，然后参考所给的数组(array-like)的形状和数据类型来创建一个新的数组。
    所以就full-like来说就需要我们传一个已知的数组，然后该方法参考该已知数组的形状和数据类型，然后用指定的填充值进行填充，最后返回一个形状和数据类型都与参考数组相同的新数组(值为指定的填充值)。

2、数组操作常用

### 前言：
    然后接下来文档中就是介绍数组操作常用部分了，然后官方文档也很好地对相关方法做了归类，我们参考归类来学习了解即可。
    学习链接：https://numpy.org/doc/stable/reference/routines.array-manipulation.html。
    
    
### Basic operations(基础操作)
(1) np.copyto(dst,src[,casting,where]):
    复制一个数组的值到另一个数组中，建立在二者可广播的基础上(否则会报错)
    dst：即destination目的地，表示目标数组的意思。
    src：即source资源，表示源资源数组的意思。
    其他参数自行了解
(2) np.shape(a)：
    返回给定数组的形状信息元组
    a：即array数组，表示给定数组


### Changing array shape(改变数组形状)
(1) np.reshape(a,newshape,order='C')：
    重定义指定数组的形状并返回
    a：即array数组，表示给定数组
    newshape：新的形状，可以是一个整数(一维)或者一个元组
    order：可选值有"C"(C-like index order)、"F"( Fortran-like index order)、"A"，具体含义可以参考后面的补充内容
(2) np.ravel(a,order="C")：
    返回一个连续的扁平化数组(使一维化)
    a：即给定数组
(3) np.ndarray.flat：
    以一维化的可迭代对象(numpy.flatiter)覆盖原数组
    numpy数组对象可以直接使用该方法实现扁平化
(4) np.ndarray.flatten(order="C")：
    返回一个由给定数组一维化(扁平化)的数组副本
    与np.ndarray.flat不同的是，其一是np.ndarray.flat是覆盖原数组而该是原数组的副本，其二返回的类型不同，np.ndarray.flat返回的是可迭代对象而该是返回数组对象。



### Transpose-like operation(类转置操作)
(1) np.moveaxis(a,source,destination)：
    顾名思义，即移动轴(即维度)，移动轴就会改变原数组的数据位置和形状特征
    a：即数组
    source：一个整数或整数序列，表示源数组要移动位置的轴
    destination：一个整数或整数序列，表示指定轴移动后的目标对应位置
(2) np.rollaxis(a,axis,start=0)：
    顾名思义，即滚动轴(即维度)，轴位置变换会改变原数组的数据位置和形状特征
    a：即数组
    axis：一个整数，指定要滚动的位置轴
    start：一个整数，它和axis决定了被移动的轴最终的位置，如果start<=axis那么滚动到指定整数索引位置，如果start>axis那么滚动到(指定整数-1)的索引位置。
(3) np.swapaxes(a,axis1,axis2)：
    顾名思义，即交换轴(即维度)，交换轴从而改变对应原数组中的元素位置
    a：即数组
    axis1：第一个轴
    axis2：第二个轴
    维度多了轴变化可能并不能很好的直接看出变换后的数组样子，但是只需要明白比如三维数组一个元素可以表示为(x,y,z)，然后我交换第一个轴x和最后一个轴z，则这个元素的坐标位置将会变换到(z,y,x)，其他多维的类似。
(4) ndarray.T：
    返回一个转置后数组的视图(view)，视图是一种浅拷贝(可以参考后面"视图"补充内容)。
    转置其实就是对轴进行倒转
(5) np.transpose(a,axes=None)：
    这是一个集转置和顺序排列轴的一个方法，将会返回轴变化后的一个数组对象
    a：即数组
    axes：一个整数元组或者列表，元组或者列表中的整数元素作为索引对应着轴，元素的个数要求必须和轴个数保持一致(否则会报错)。
    

### Changing number of dimensions(改变维度数)
(1) np.atleast_1d(*arys)：
    用于生成创建新数组，至少一维的
    arys：一个或多个输入数组(不一定是必须是数组，可以是满足数组结构的序列)
(2) np.atleast_2d(*arys)/np.atleast_3d(*arys)：
    同样也是用于生成创建新数组，至少二、三维的
(3) np.broadcast(int1,int2,...)：
    返回一个模仿广播的对象
    int1：类数组类型
(4) broadcast_to(array,shape,[subok])：
    广播一个数组到一个新形状
(5) broadcast_arrays(*args,[subok])：
    相互广播任意数量的数组
(6) expand_dims(a,axis)：
    扩展数组的维度
    axis：一个序列，指定要扩展轴的位置
(7) squeeze(a,axis=None)：
    返回一个移除指定轴的新数组
    a：即数组
    axis：一个整数或者整数元组，表示指定要移除的轴，默认为None(移除轴长度为1的轴)


### Changing kind of array(改变数组类型)
(1) np.asarray(a,dtype=None,order=None,*,like=None)：
    用于把输入转为一个指定格式的数组
    a：即array_like类数组
    dtype：数据类型
    order：内存布局
(2) np.asanyarray(a,dtype=None,order=None,*,like=None)：
    将输入转换为一个数组，但是要求传递是一个ndarray子类
(3) np.asmatrix(data,dtype=None)：
    将输入解释转换为一个矩阵
    data：类数组类型，要转换的数据
(4) np.asfarray(a,dtype=np.double)
    将给定类数组类型转换为一个浮点型的数组对象并返回，"asf"即as float的意思
(5) np.asfortranarray(a,dtype=None,*,like=None)：
    将给定的类数组转换为一个内存布局为Fortran order的数组对象并返回
(7) np.ascontiguousarray(a,dtype=None,*,like=None)：
    将给定的类数组转换为一个内存布局为C order的数组对象并返回
(8) np.asarray_chkfinite(a,dtype=None,order=None)：
    将给定的类数组转换为一个数组对象并返回，转换时会检查值是否为NaNs或者Infs(成立则报出ValueError)
(9) np.require(a,dtype=None,requirements=None,*,like=None)：
    根据给定类数组和给定的要求(requirements)，返回一个满足要求的数组对象
    requirements可选值及其含义如下：
    ‘F_CONTIGUOUS’ (‘F’) - ensure a Fortran-contiguous array
    ‘C_CONTIGUOUS’ (‘C’) - ensure a C-contiguous array
    ‘ALIGNED’ (‘A’) - ensure a data-type aligned array
    ‘WRITEABLE’ (‘W’) - ensure a writable array
    ‘OWNDATA’ (‘O’) - ensure an array that owns its own data
    ‘ENSUREARRAY’, (‘E’) - ensure a base array, instead of a subclass
    
    
### Joining arrays(连接数组)
(1) np.concatenate((a1,a2,...),axis=0,out=None,dtype=None,casting="same_kind")：
    a1,a2,...：类数组序列
    axis：整型，按照指定的轴进行拼接
    casting：控制可能发生哪种类型的数据强制转换，默认为'same_kind'(具体参考后面casting参数)

(2) np.stack(array[,axis,out,dtype,casting])：
    堆叠
(3) np.hstack(tup,*[,dtype,casting])：
    水平堆叠
(4) np.vstack(tup,*[,dtype,casting])：
    竖直堆叠
(5) np.column_stack(tup)：
    列堆叠
(6) np.row-stack(tup,[*[,dtype,casting]])：
    行堆叠
(7) np.block(arrays)：
    arrays：嵌套的类数组元素列表(不能是元组)
    根据所给的块列表组装为一个多维数组并返回

    

### Splitting arrays(分割数组)
前言：
    首先从设计角度上来说，要求拆分后的维度与源数组保持一致，拆分从形象的几何上来说就是在整个元素集几何图上画分割线从而来进行拆分。
    需要着重说明的是，我暂时没有学习到混合拆分(就是可以同时画横和纵向分割线)，但是就功能实现角度来说，应用已有的方法也是能实现的。
    另外拆分是允许我们拆分为不限于二份而是多份新数组的（允许我们画多个分割线）。
(1) np.split(ary,indices_or_sections[,axis])：
    ary：要被分割的数组
    indices_or_sections：索引序列或分段数，分段数即一个整数表示数组最终被均分成的段数(如果不能均分则会报错)，索引序列抽象为要在指定索引位置画分割线对数组进行分割。

(2) np.array_split(ary,indices_or_sections,axis=0)：
    与np.split仅有一点不同，就是将如果不能按照指定段数均分，则少了就把剩余作为最后一段、多了就把多余添加到首段中(并不会报错)。
(3) dsplit(ary,indices_or_sections)
(4) hsplit(ary,indices_or_sections)：
    横向拆分
(5) vsplit(ary,indices_or_sections)：
    纵向拆分
    


### Tiling arrays(铺数组瓷砖)
    可以把一个数组看做一块瓷砖，瓷砖(数组)是相同的(同一个)，然后我们可以横纵向(多维)进行铺这些瓷砖，确实很像生活中铺瓷砖。
(1) np.tile(a,reps)：
    返回一个规律极其块化的新扩展数组
    a：即要作为瓷砖的数组
    reps：即repeats要重复的数量，可以是一个整数表示在当前维度下扩展，可以是一个整数数组表示多维度扩展
(2) np.repeats(a,reps,axis=None)：
    重复铺数组中的每个轴元素(所谓轴元素就是同纬度的所有元素)，重复后的元素是紧跟原轴元素其后的，给以给定元素对应重复的次数(reps)，还可以指定重复铺的方向(行还是列)，注意最高支持二维度(超过二维度该方法报错)。
    reps：可以是一个整数表示每个轴元素的重复数，可以是一个列表表示对应的轴元素重复数
    axis：默认为None使结果集为扁平化数组，可以是一个整数表示轴元素重复后的维度(最高2维度)


### Adding and removing elements(增加和移除元素)
    注意以下的这些方法，都是返回新数组(并不是修改原数组)，要特别注意的是axis参数和values参数。
(1) np.delete(arr,obj,axis=None)：
    删除指定数组中指定索引的元素或者轴元素，然后返回一个新数组
    obj：切片或整数或者序列，表示索引对应的元素或者轴元素(具体参考axis参数)
    axis：默认为None表示把原数组看成一个扁平数组(返回也将是一个扁平数组)，此时obj就是以元素为单位，可以是一个整数表示指定原数组中的轴维度此时obj就以轴元素为单位。
(2) np.insert(arr,obj,values,axis=None)：
    values：类数组类型表示要插入的值，具体维度需参考axis参数(与axis对应的元素保持一致，否则会报错)
    obj：需要补充的是，该序列中可以有重复索引整数值表示重复插入
(3) np.append(arr,values,axis=None)：
    数组末尾追加值
    参数参考前面类似即可，需要注意的是依然要求values和axis维度保持一致
(4) np.resize(a,new_shape)：
    这个不是resize吗？确实是一个形状修改的方法，但也做了一些优化，就是你给的形状超出了原数组元素集时就有一个填充策略(C-order)，所以这也勉强算作添加方法。
    new_shape：一个shape元组，就不多说了
(5) np.trim_zeros(filt,trim='fb')
    这个方法顾名思义就是删除数组前后的零元素，需要注意的是要求被作用输入(数组或者序列)必须是一维的
    filt：这个参数意思不明确，但是知道是被作用输入(数组或序列)即可。
    trim：默认为"fb"表示前后零元素都将被删除，"f"即front、"b"即back，所以可选值有三个"b"、"f"、"fb"
(4) np.unique(a,return_index=False,return_inverse=False,return_counts=False,axis=None,*,equal_nan=True)：
    方法参数很多，但是用意却很好理解，就是返回一个数组包含了指定数组中的唯一值。
    然后这个方法有很多参数，其中三个return_*是布尔类型的表示是否返回对应的unique值信息，如果指定了True，那么返回的结果就是一个元组(你应该用多个变量来接收，当然返回的顺序和参数顺序是一致的)。
    最后axis参数设计的目的是轴化(操作到轴元素级别)，当然默认值还是None表示扁平化(此时对应的操作时元素级别的)。
    
    

### Rearranging elements(重排元素)。
(1) np.flip(m,axis=None)：
    倒转指定数组中的轴元素并返回
    m：表示manipulated被操作的类数组类型。
    axis：需要注意的是这个axis默认值None虽然也是扁平化数组操作(元素级)，但是返回的数组并不是扁平化的(而是与原数组保持一致)
(2) np.fliplr(m)：
    应用于二维数组的方法，水平倒转数组中的轴元素(axis=1)并返回fliplr中的"lr"表示"left to right"即水平反转。
(3) np.flipud(m)：
    应用于二维数组的方法，竖直倒转数组中的轴(axis=0)并返回fliplr中的"lr"表示"up to down"即竖直反转。
(4) np.reshape(a,newshape,order='C')：
    不改变指定数组的值，修改其为指定形状，如果形状积与原数组元素集不一致将会报错。
(5) roll(a,shift,axis=None)：
    根据指定轴滚动数组元素
    shift：一个整数表示即要滚动的偏移量(正数表示向后滚动，负数表示是向前)，也可以是一个整数序列对应参考axis序列参数表示对应轴滚动的偏移量。
    axis：默认为None表示扁平化滚动操作，但注意返回的数组维度依然与给定数组一致   
(6) rot90(m,k=1,axes=(0,1))：
    90度旋转指定数组元素，rot即"rotate"的意思，所谓旋转需要两个参考量(旋转面和转角度)
    k：表示旋转90度的个数，正数表示逆时针旋转，负数表示顺时针旋转
    axes：一个二元素数组，这个参数用于确定旋转面(两个维度确定一个旋转面)，同时维度先后顺序也作用于旋转顺序，

ufunc

### ufunc属性
ufunc.nin：nin即n-input的缩写，获取输入参数的个数
ufunc.nout：nout即n-output的缩写，获取输出参数的个数
ufunc.nargs：也是获取输入参数的个数，要注意的是会比ufunc.nin多1，因为有个默认参数out
ufunc.ntypes：获取输入参数支持的类型的总数量
ufunc.types：返回一个列表描述输入到输出的类型，参考后面的“类型字符”
ufunc.identity：返回给定方法对应数据类型的单位元素
ufunc.signature：返回一个字符串描述了它的输入参数和输出结果的形状类型
ufunc.reduce：用于数组逐元素聚合运算
ufunc.accumulate：用于对数组中元素进行累积运算
ufunc.reduceat：用于指定的索引位置上对数组进行分段的累积操作
ufunc.outer：用于计算两个数组元素构成的外积
ufunc.at：根据指定的索引和操作对数组进行原子操作
提示：具体示例直接参考文档中即可

### 类型字符：
'?'：布尔型
'b'：有符号字节型（int8）
'B'：无符号字节型（uint8）
'h'：有符号短整型（int16）
'H'：无符号短整型（uint16）
'i'：有符号整型（int32）
'I'：无符号整型（uint32）
'l'：有符号长整型（int64）
'L'：无符号长整型（uint64）
'q'：有符号长长整型（int64，仅在64位平台上）
'Q'：无符号长长整型（uint64，仅在64位平台上）
'f'：单精度浮点型（float32）
'd'：双精度浮点型（float64）
'g'：本地平台的本地C字节型（如C的char类型）
'F'：复数，由两个单精度浮点数表示（float32）
'D'：复数，由两个双精度浮点数表示（float64）
'G'：复数，由两个本地平台的本地C字节型表示
'O'：Python对象（object）

三、numpy基本操作

开篇探索

### 维度：
        维度从几何角度不是很好理解，既然数组中有类比维度概念，我们可以结合数组来理解并学习。
        我们暂且称数组表示符号"[]"为容器，如果仅有一个容器，如[el1,el2,...]，那么毫无疑问这是一维数组。
        然后我们知道二维数组类似这样：[[el1,el2],[el3,el4],...]，也就是说有子容器嵌套一层就是二维数组。
        那么子容器嵌套多层就是多维数组了，总容器级别数就可以称为维度数。

        确实像数组概念那样从容器角度来说能够更好地解析维度，比如说我拿一个纸箱A，让你说这是几维的，毫无疑问是3维(常说三维立体)，然后我再拿一个纸箱B，将纸箱A(较小)放在纸箱B里面，这时我们从纸箱B往里面看可以看到较小的纸箱A，让你再说这是几维的，我觉得你应该说4维合适。我也觉得像示例中说的，维度多了并不好理解。

数据类型

1.了解

Numpy 的类型	C 的类型	描述
np.bool	bool	存储为字节的布尔值（True或False）
np.byte	signed char	平台定义
np.ubyte	unsigned char	平台定义
np.short	short	平台定义
np.ushort	unsigned short	平台定义
np.intc	int	平台定义
np.uintc	unsigned int	平台定义
np.int_	long	平台定义
np.uint	unsigned long	平台定义
np.longlong	long long	平台定义
np.ulonglong	unsigned long long	平台定义
np.half / np.float16		半精度浮点数：符号位，5位指数，10位尾数
np.single	float	平台定义的单精度浮点数：通常为符号位，8位指数，23位尾数
np.double	double	平台定义的双精度浮点数：通常为符号位，11位指数，52位尾数。
np.longdouble	long double	平台定义的扩展精度浮点数
np.csingle	float complex	复数，由两个单精度浮点数（实部和虚部）表示
np.cdouble	double complex	复数，由两个双精度浮点数（实部和虚部）表示。
np.clongdouble	long double complex	复数，由两个扩展精度浮点数（实部和虚部）表示。

2.内存固定大小

Numpy 的类型	C 的类型	描述
np.int8	int8_t	字节（-128到127）
np.int16	int16_t	整数（-32768至32767）
np.int32	int32_t	整数（-2147483648至2147483647）
np.int64	int64_t	整数（-9223372036854775808至9223372036854775807）
np.uint8	uint8_t	无符号整数（0到255）
np.uint16	uint16_t	无符号整数（0到65535）
np.uint32	uint32_t	无符号整数（0到4294967295）
np.uint64	uint64_t	无符号整数（0到18446744073709551615）
np.intp	intptr_t	用于索引的整数，通常与索引相同 ssize_t
np.uintp	uintptr_t	整数大到足以容纳指针
np.float32	float
np.float64 / np.float_	double	请注意，这与内置python float的精度相匹配。
np.complex64	float complex	复数，由两个32位浮点数（实数和虚数组件）表示
np.complex128 / np.complex_	double complex	请注意，这与内置python 复合体的精度相匹配。

3.类型指定

简要：
使用dtype关键字参数作为数组创建时的一个类型指定，推荐使用实例类型方式(参考举例)

举例：
z = np.arange(3, dtype=np.uint8)
z = np.array([1, 2, 3], dtype='f')
z = np.arange(3, dtype=np.uint8)

5. 数据类型修改(转换)

简要：
3.1 arr.astype(type)：astype方法指定type参数来转换为目标类型数组
3.2 np.npType(arr)：将数组作为numpy类型实例参数，从而实现类型转换


举例：
>>> z.astype(float)                 
array([  0.,  1.,  2.])
>>> np.int8(z)
array([0, 1, 2], dtype=int8)

6. 查看类型

简要：
arr.dtype属性查看指定数组对象的类型

7.类型范围

简要：
1. np.iinfo：前缀i(int)，即获取整型相关numpy类型的范围信息
2. np.finfo：前缀f(float)，即获取浮点型相关的numpy类型的范围信息

举例：
>>> np.iinfo(np.int32)
iinfo(min=-2147483648, max=2147483647, dtype=int32)
>>> np.finfo(np.float32)
finfo(resolution=1e-06, min=-3.4028235e+38, max=3.4028235e+38, dtype=float32)

8.补充

NumPy的人都知道：
int是指np.int_，
bool意味着np.bool_，
float是np.float_，
complex是np.complex_。
其他数据类型没有Python等价物。

创建数组

创建数组有5种常规机制

1. 从其他Python结构（例如，列表，元组）转换
2. numpy原生数组的创建（例如，arange、ones、zeros等）
3. 从磁盘读取数组，无论是标准格式还是自定义格式
4. 通过使用字符串或缓冲区从原始字节创建数组
5. 使用特殊库函数（例如，random）

常用创建方法

方法	功能
`numpy.array`	从Python列表或元组创建一个多维数组
`numpy.zeros`	创建一个给定形状的数组，并将所有元素初始化为0
`numpy.zeros_like`	创建一个与给定数组具有相同形状的数组，并将所有元素初始化为0
`numpy.ones`	创建一个给定形状的数组，并将所有元素初始化为1
`numpy.ones_like`	创建一个与给定数组具有相同形状的数组，并将所有元素初始化为1
`numpy.empty`	创建一个给定形状的数组，但不初始化元素值
`numpy.empty_like`	创建一个与给定数组具有相同形状的数组，但不初始化元素值
`numpy.arange`	创建一个按指定范围和步长的等差数组
`numpy.linspace`	运算慢创建一个在指定范围内具有指定数量的等间隔数组
`numpy.random.mtrand.RandomState.rand`	从均匀分布中生成随机样本，具有给定形状和范围
`numpy.random.mtrand.RandomState.randn`	从标准正态分布中生成随机样本，具有给定形状
`numpy.fromfunction`	使用用户定义的函数从函数返回的值创建数组
`numpy.fromfile`	从文件中读取数据，并根据指定的数据类型创建数组

拷贝创建

前言：
拷贝数组从某种角度来说也算创建数组，因为创建数组本质上说的是创建数组对象。
当然既然是拷贝就有：深拷贝和浅拷贝(二者区别自了解)。

方法：
1 浅拷贝：
1.1 arr.view()
1.2 切片(返回一个视图)
2 深拷贝
arr.copy()


代码示例：
>>> a = np.random.randint(0,10,(2,3))
>>> a
array([[2, 4, 9],
       [4, 5, 4]])
       
>>> b = a.view()
>>> b
array([[2, 4, 9],
       [4, 5, 4]])
>>> b[0] = 1
>>> b
array([[1, 1, 1],
       [4, 5, 4]])
>>> a
array([[1, 1, 1],
       [4, 5, 4]])
       
>>> c = a[0,:]
>>> c
array([1, 1, 1])
>>> c[:] = 2
>>> c
array([2, 2, 2])
>>> a
array([[2, 2, 2],
       [4, 5, 4]])

数组运算

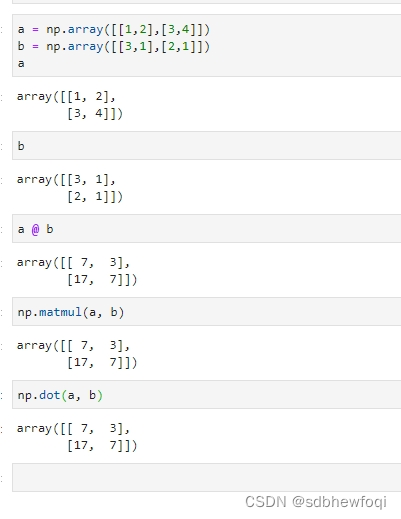
1.算数运算：
+、-、*、/、%、**
numpy.add()
numpy.subtract()
numpy.multiply()
numpy.divide()
numpy.power()
numpy.remainder()


2.数组的比较和逻辑运算：
==、!=、>、>=、<、<=
逻辑与：numpy.logical_and()
逻辑或：numpy.logical_or()
逻辑非：numpy.logical_not()


4.数组的聚合统计运算：
求和：numpy.sum()
求最大值：numpy.max()
求最小值：numpy.min()
求均值：numpy.mean()
求中位数：numpy.median()
求标准差：numpy.std()
求方差：numpy.var()
求积：numpy.prod()
求和累积：numpy.cumsum()
求积累积：numpy.cumprod()
求最大值的索引：numpy.argmax()
求最小值的索引：numpy.argmin()



5.矩阵运算：
矩阵乘法：numpy.matmul() 或 @
矩阵转置：numpy.transpose()
矩阵求逆：numpy.linalg.inv()
矩阵行列式：numpy.linalg.det()


6.其他运算：
求绝对值：numpy.abs()
求指数函数：numpy.exp()
求自然对数：numpy.log()
求正弦函数：numpy.sin()
求余弦函数：numpy.cos()
求平方根：numpy.sqrt()
逐元素向下取整：numpy.floor()

形状操作

查看形状

说明：使用数组对象的shape属性
用法：arr.shape

形状变换

方法：
扁平一维化：ravel()
形状重构：reshape()
形状重构(源数组)：resize()
矩阵转置：T


理解分析：
(1) 像ravel到reshape/resize再到split方法，即普通到复杂再到特殊的转换过程（互补）
(2) 形状重构有两个相关方法，主要区别就是新数组还是源数组操作（同样的功能不同的业务目的）

形状合并

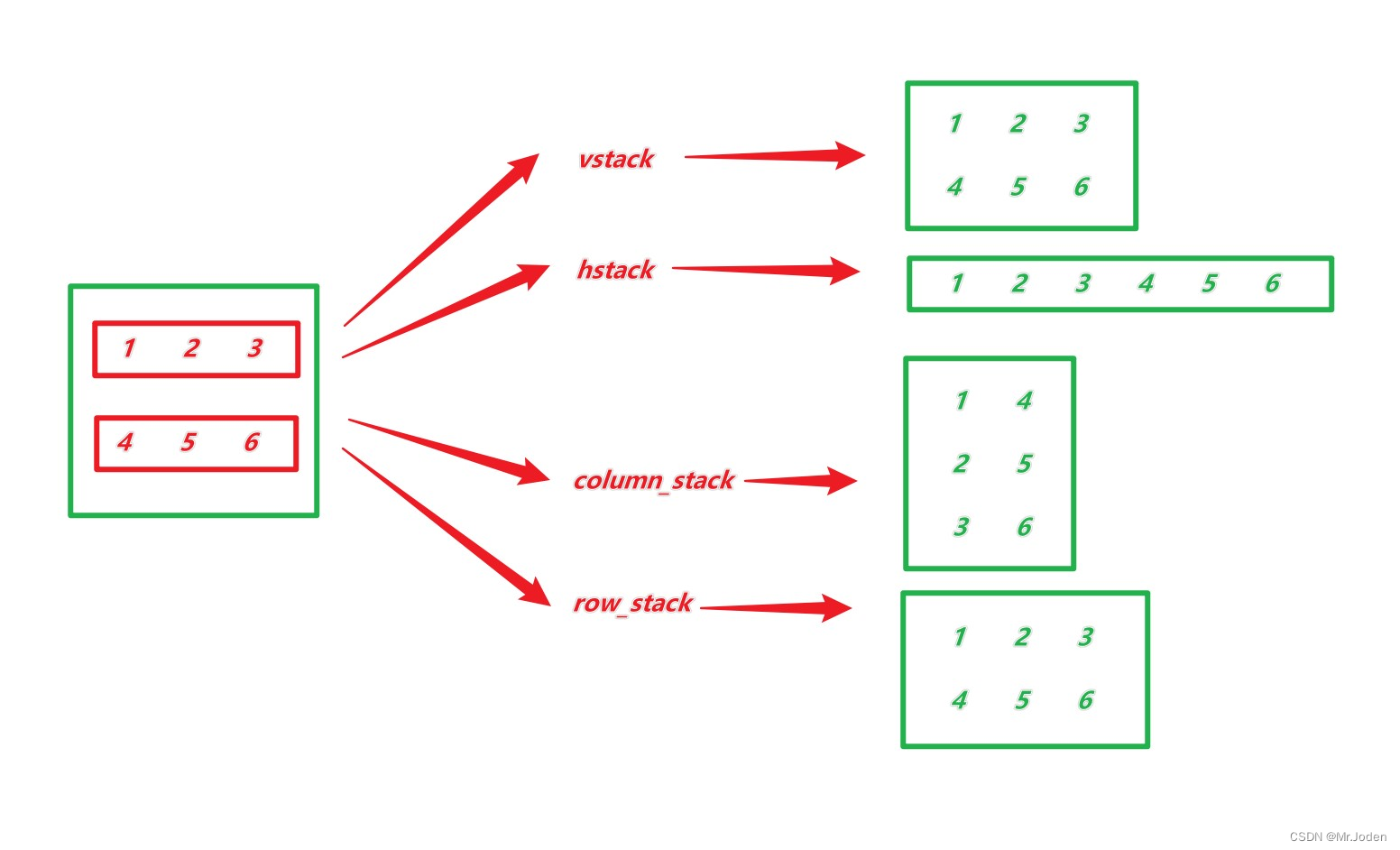
方法：
纵向堆叠：np.vstack()
横向堆叠：np.hstack()
元素列堆叠：np.column-stack()
元素行堆叠：np.row-stack()
数组拼接：np.concatenate()


理解分析：
对于v/h开头的堆叠方法和column/row开头的堆叠方法，是面对整体和面对元素的区别（设计角度不同）


代码示例：
>>> a = np.floor(np.random.random((2,2))*10)
>>> a
array([[7., 9.],
       [4., 1.]])
>>> b = np.floor(np.random.random((2,2))*10)
>>> b
array([[8., 4.],
       [6., 8.]])
>>> np.hstack((a,b))
array([[7., 9., 8., 4.],
       [4., 1., 6., 8.]])
>>> np.column_stack((a,b))
array([[7., 9., 8., 4.],
       [4., 1., 6., 8.]])
>>> np.concatenate((a,b),axis=1)
array([[7., 9., 8., 4.],
       [4., 1., 6., 8.]])

形状拆分

前言：
(1) 首先从设计角度上来说，要求拆分后的维度与源数组保持一致，拆分从形象的几何上来说就是在整个元素集几何图上画分割线从而来进行拆分。
(3) 需要着重说明的是，我暂时没有学习到混合拆分(就是可以同时画横和纵向分割线)，但是就功能实现角度来说，应用已有的方法也是能实现的。
(4) 另外拆分是允许我们拆分为不限于二份而是多份新数组的（允许我们画多个分割线）。


方法：
拆分：np.spilt()
纵向拆分：np.vsplit()
横向拆分：np.hsplit()
深度拆分：np.dsplit()

特殊

在这里主要有几个特殊的用法需要单独列出来学习，有np.r_、np.c_。
在np.r_或者np.c_后跟"[]"来进行构建数组。
那么在"[]"中可以写什么呢？可以有：切片、重复片段、标量常数
切片：整数切片，表示范围值，

Numpy学习(参考)

一、前言

二、numpy官方文档

文档划分

参数规范

相关知识明知

Routines学习(部分)

1、创建

2、数组操作常用

ufunc

三、numpy基本操作

开篇探索

数据类型

创建数组

创建数组有5种常规机制

常用创建方法

拷贝创建

数组运算

形状操作

查看形状

形状变换

形状合并

形状拆分

特殊

相关文章