内容 隐藏
一、性能数据函数耗时采集及可视化报表生成
1. 性能数据文件保存(cProfile)
2. 详细性能数据读取查看
二、生成函数调用栈结构图(gprof2dot)教程
三、性能分析及优化实战
四、耗时异常自动化监控
1. 正态分布数据方案
2. Turkey 箱型图方案
本文内容包括Python性能可视化分析,逻辑优化,及根据不同的模型动态计算安全阈值,实现各个函数耗时及程序总耗时的自动化监控预警。
在做Python性能分析优化的时候,可以借助cProfile生成性能数据文件,通过pstats获取详细耗时分布数据,结合gprof2dot脚本生成函数调用栈结构图做可视化分析,提高性能分析的效率。
接着从具体的耗时分布,先从占用大头的函数分析具体逻辑实现,逐步优化,同时保存pstats函数耗时平均值数据作为后续异常自动化监控的样本数据。
实现耗时自动化监控必须是可以根据算法动态调整安全阈值,而不是人工定死安全阈值范围,这样才可以实现异常监控的自循环和迭代校准。
一、性能数据函数耗时采集及可视化报表生成
1. 性能数据文件保存(cProfile)
首先是性能数据文件的保存,cProfile和profile提供了Python程序的确定性性能分析。profile是一组统计数据,用来描述程序的各个部分执行的频率和时间。在程序开始的时候调用enable开始性能数据采集,结束的时候调用dump_stats停止性能数据采集并保存性能数据到指定路径的文件。
import cProfile# 程序开始的时候打开数据采集开关
pr = cProfile.Profile()
pr.enable()
# 在程序运行结束的时候dump性能数据到指定路径文件中,profliePath为保存文件的绝对路径参数
pr.dump_stats(profliePath)2. 详细性能数据读取查看
保存性能数据到文件之后,可以用pstats读取文件中的数据,profile统计数据可以通过pstats模块格式化为报表。
import pstats
# 读取性能数据
pS = pstats.Stats(profliePath)
# 根据函数自身累计耗时做排序
pS.sort_stats('tottime')
# 打印所有耗时函数信息
pS.print_stats()
print_stats()输出示例:
79837 function calls (75565 primitive calls) in 37.311 seconds
Ordered by: internal time
ncalls tottime percall cumtime percall filename:lineno(function)
2050 30.167 0.015 30.167 0.015 {time.sleep}
16 6.579 0.411 6.579 0.411 {select.select}
1 0.142 0.142 0.142 0.142 {method 'do_handshake' of '_ssl._SSLSocket' objects}
434 0.074 0.000 0.074 0.000 {method 'read' of '_ssl._SSLSocket' objects}
1 0.062 0.062 0.062 0.062 {method 'connect' of '_socket.socket' objects}
37 0.046 0.001 0.046 0.001 {posix.read}
14 0.024 0.002 0.024 0.002 {posix.fork}输出字段说明:
- ncalls 函数被调用次数(只有一个数字时表示不存在递归,有斜杠分割数字时,后面的数字表示非递归调用的次数)
- tottime 函数总计运行时间,不包括子函数调用时间
- percall 函数运行一次的平均时间,等于tottime/ncalls
- cumtime 函数总计运行时间,包括子函数调用时间
- percall 函数运行一次的平均时间,等于cumtime/ncalls
- filename:lineno(function) 函数所在的文件名,函数的行号,函数名或基础框架函数类
如果要获取print_stats()里面各个字段信息可以通过如下方式:
# func————filename:lineno(function)
# cc ———— call count,调用次数
# nc ———— ncalls
# tt ———— tottime
# ct ———— cumtime
# callers ———— 调用堆栈数组,每项数据包括了func, (cc, nc, tt, ct) 字段
for index in range(len(pS.fcn_list)):
func = pS.fcn_list[index]
cc, nc, tt, ct, callers = pS.stats[func]
print cc, nc, tt, ct, func, callers
for func, (cc, nc, tt, ct) in callers.iteritems():
print func,cc, nc, tt, ct二、生成函数调用栈结构图(gprof2dot)教程
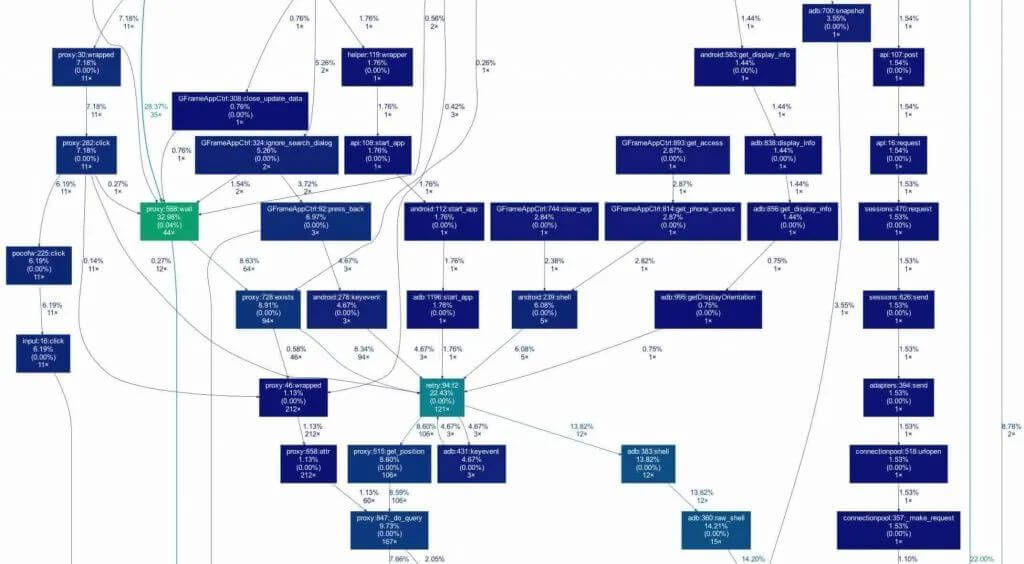
gprof2dot脚本把gprof或callgrind分析获得的信息,转化成一个以DOT语言描述的程序调用有向图对象,再通过Graphviz将DOT有向图对象渲染成图片,这样就可以很直观地看出整个程序的调用栈,包括函数所在的类和行数、耗时占比、函数递归次数、以及被调用的次数。
先从GitHub上下载gprof2dot.py脚本到本地,和执行的程序的脚本文件放在同一目录下,当然要使用这个脚本还需要安装graphviz,使用brew命令安装,若安装过程中遇到异常,根据异常提示执行命令安装需要的工具
brew install graphviz生成程序函数调用栈结构图的逻辑可以参考如下逻辑实现,具体根据自身需求做下修改。
import os# 获取当前gprof2dot.py脚本路径
gprof2dotPath = os.path.join(os.path.dirname(os.path.abspath(__file__)), 'gprof2dot.py')# 函数调用栈结构图保存文件名路径,这边使用生成PNG图片结果
dumpProfPath = profliePath.replace("stats", "png")
dumpCmd = "python %s -f pstats %s | dot -Tpng -o %s" % (gprof2dotPath, profliePath, dumpProfPath)
os.popen(dumpCmd)三、性能分析及优化实战
在生成函数调用栈结构图之后,就可以很容易的看出各个函数之间的调用关系,每个方块内包括的信息包括函数所在的类和行数,耗时百分比和被调用次数,如果这个函数存在递归的情况,方块边缘会有一个回旋的箭头标明递归的次数。
从结构图里面找到耗时占用较多的部分,分析具体函数的实现逻辑,定位具体耗时的原因,优化的策略如下:
- 去除多余的逻辑:去除冗余代码
- 优化递归函数:加日志打印递归时候的各个参数,如果发现很多参数都是重复的,可以加缓存,避免多余的递归消耗。
- 归并通用逻辑调用:一个函数多次调用同一个子函数获取参数,查看这个子函数的调用是否可以进行整合归并,避免多余的函数调用。
- 通过上下文环境判断测试程序的初始化是否必要,非必要情况下不进行测试环境的重置操作。
四、耗时异常自动化监控
如果是通过历史的耗时数据计算得到平均值+固定浮动百分比的方式,来配置耗时安全阈值参数实施异常监控存在很大的问题,因为函数执行的耗时容易受设备和运行环境的影响,人工固定浮动百分比的方式维护性差,数据本身不可迭代自循环,总不能每次出现误报问题之后都去手动调整参数。
这边监控的维度包括两方面,一方面是程序各个函数执行耗时的平均值,另一方面是完整程序执行的总耗时,在前期先把这些历史耗时数据保存在数据库中,供后续自动化异常监控的实现提供样本数据。
要实现自动化阈值调整,需要借助常规的模型算法实现,这边只对耗时单个维度的异常做自动化监控实现。
根据原理,无监督异常检测模型一般可分为以下几类:
- 基于统计和概率模型:主要是对数据的分布做出假设,并找出假设下所定义的“异常”;
- 线性模型:主要思想是通过线性方法找到合适的低维子空间使得异常点在其中区别于正常点;
- 基于距离:这种方法认为异常点距离正常点比较远,通过比较数据点之间的距离区分异常点;
- 基于密度:由于数据分布不均匀,绝对距离无法衡量数据点之间相对远近时,用局部密度表示数据点的异常情况;
- 基于聚类:将数据点聚类,不属于任何簇、距离最近的簇较远、稀疏聚类里的点认为是异常点;
- 基于树:通过划分子空间构建树模型寻找异常点。
异常耗时数据是波动的一维数据,这边就直接采用基于统计和概率模型的方式,根据保存的历史数据判断数据是否符合正态分布。
若符合正态分布则用 μ+3δ(平均值+3倍标准差)的方式计算得到安全阈值;
若不符合正态分布,则用Turkey 箱型图方案 Q+1.5IQR 计算安全阈值。
根据实际测试来看,随着样本数据的增加,会出现前期符合正态分布的函数耗时曲线,随着样本数据的增加会变成不符合正态分布。
Python中用于判断数据是否符合正态分布的代码如下,当pvalue值大于0.05时为正态分布,dataList是耗时数组数据:
from scipy import stats
import numpy
percallMean = numpy.mean(dataList) # 计算均值
# percallVar = numpy.var(dataList) # 求方差
percallStd = numpy.std(dataList) # 计算标准差
kstestResult = stats.kstest(dataList, 'norm', (percallMean, percallStd))
# 当pvalue值大于0.05为正态分布
if kstestResult[1] > 0.05:
pass1. 正态分布数据方案

在统计学中,如果一个数据分布近似正态,那么大约 68% 的数据值会在均值的一个标准差范围内,大约 95% 会在两个标准差范围内,大约 99.7% 会在三个标准差范围内。因此,如果任何数据点超过标准差的 3 倍,那么这些点很有可能是异常值或离群点。即正态分布的安全阈值上限为:percallMean + 3 * percallStd
2. Turkey 箱型图方案
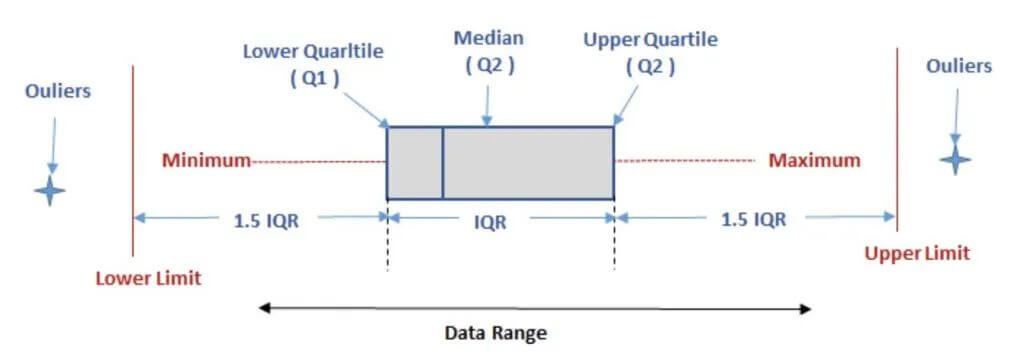
基于正态分布的 3σ 法则或 Z 分数方法的异常检测是以假定数据服从正态分布为前提的,但实际数据往往并不严格服从正态分布。应用这种方法于非正态分布数据中判断异常值,其有效性是有限的。Tukey 箱型图是一种用于反映原始数据分布的特征常用方法,也可用于异常点识别。在识别异常点时其主要依靠实际数据,因此有其自身的优越性。
箱型图为我们提供了识别异常值的一个标准:异常值被定义为小于 Q1-1.5IQR 或大于 Q+1.5IQR 的值。虽然这种标准有点任意性,但它来源于经验判断,经验表明它在处理需要特别注意的数据方面表现不错。
计算箱型图安全阈值Python实现逻辑如下:
import numpy
percallMean = numpy.mean(dataList) # 计算均值
boxplotQ1 = numpy.percentile(dataList, 25)
boxplotQ2 = numpy.percentile(dataList, 75)
boxplotIQR = boxplotQ2 - boxplotQ1
upperLimit = boxplotQ2 + 1.5 * boxplotIQR在程序实现中就是,在一个程序或用例执行完毕之后,先拿历史数据判断是否符合正态分布,当然历史样本数据至少要达到20个才比较准确,小于20个的时候就继续收集数据,不做异常判断。根据正态分布模型或箱型图模型计算安全阈值参数,判断当前各个函数耗时平均值或用例总耗时是否超过阈值,超过则预警。

高斯模型和箱型图两种方式阈值范围对比
这边给出stats文件数据汇总解析之后,根据相应的模型绘制耗时曲线及阈值或正态曲线及阈值的代码实现,statFolder参数替换成自己stats文件所在文件夹即可。
# coding=utf-8
import os
import pstats
import matplotlib
matplotlib.use('Agg')
import matplotlib.pyplot as plt
import traceback
from scipy import stats
import numpy
"""汇总函数耗时平均值数据
"""
def dataSummary(array, fileName, fcn, percall):
(funcPath, line, func) = fcn
exists = False
for item in array:
if item["func"] == func and item["funcPath"] == funcPath and item["line"] == line:
exists = True
item["cost"].append({
"percall": percall,
"fileName": fileName
})
if not exists:
array.append({
"func": func,
"funcPath": funcPath,
"line": line,
"cost": [{
"percall": percall,
"fileName": fileName
}]
})
"""
高斯函数计算Y值
"""
def gaussian(x, mu, delta):
exp = numpy.exp(- numpy.power(x - mu, 2) / (2 * numpy.power(delta, 2)))
c = 1 / (delta * numpy.sqrt(2 * numpy.pi))
return c * exp
"""
读取汇总所有stats文件数据
"""
def readStatsFile(statFolder, filterData):
for path, dir_list, file_list in os.walk(statFolder, "r"):
for fileName in file_list:
if fileName.find(".stats") > 0:
fileAbsolutePath = os.path.join(path, fileName)
pS = pstats.Stats(fileAbsolutePath)
# 先对耗时数据从大到小进行排序
pS.sort_stats('cumtime')
# pS.print_stats()
# 统计前100条耗时数据
for index in range(100):
fcn = pS.fcn_list[index]
(funcPath, line, func) = fcn
# cc ———— call count,调用次数
# nc ———— ncalls,调用次数(只有一个数字时表示不存在递归;有斜杠分割数字时,后面的数字表示非递归调用的次数)
# tt ———— tottime,函数总计运行时间,除去函数中调用的子函数运行时间
# ct ———— cumtime,函数总计运行时间,含调用的子函数运行时间
cc, nc, tt, ct, callers = pS.stats[fcn]
# print fileName, func, cc, nc, tt, ct, callers
percall = ct / nc
# 只统计单次函数调用大于1毫秒的数据
if percall >= 0.001:
dataSummary(filterData, fileName, fcn, percall)
"""
绘制高斯函数曲线和安全阈值
"""
def drawGaussian(func, line, percallMean, threshold, percallList, dumpFolder):
plt.title(func)
plt.figure(figsize=(10, 8))
for delta in [0.2, 0.5, 1]:
gaussY = []
gaussX = []
for item in percallList:
# 这边为了呈现正态曲线效果,减去平均值
gaussX.append(item - percallMean)
y = gaussian(item - percallMean, 0, delta)
gaussY.append(y)
plt.plot(gaussX, gaussY, label='sigma={}'.format(delta))
# 绘制水位线
plt.plot([threshold - percallMean, threshold - percallMean], [0, 5 * gaussian(percallMean, 0, 1)], color='red',
linestyle="-", label="Threshold:" + str("%.5f" % threshold))
plt.xlabel("Time(s)", fontsize=12)
plt.legend()
plt.tight_layout()
# 可能不同类中包含相同的函数名,加上行数参数避免覆盖
imagePath = dumpFolder + "cost_%s_%s.png" % (func, str(line))
plt.savefig(imagePath)
"""
绘制耗时曲线和安全阈值
"""
def drawCurve(func, line, percallList, dumpFolder):
boxplotQ1 = numpy.percentile(percallList, 25)
boxplotQ2 = numpy.percentile(percallList, 75)
boxplotIQR = boxplotQ2 - boxplotQ1
upperLimit = boxplotQ2 + 1.5 * boxplotIQR
# 不符合正态分布,绘制波动曲线
timeArray = [i for i in range(len(percallList))]
plt.title(dataItem["func"])
plt.figure(figsize=(10, 8))
# 绘制水位线
plt.plot([0, len(percallList)], [upperLimit, upperLimit], color='red', linestyle="-",
label="Threshold:" + str("%.5f" % upperLimit))
plt.plot(timeArray, percallList, label=dataItem["func"] + "_" + str(dataItem["line"]))
plt.ylabel("Time(s)", fontsize=12)
plt.legend()
plt.tight_layout()
imagePath = dumpFolder + "cost_%s_%s.png" % (func, str(line))
plt.savefig(imagePath)
if __name__ == "__main__":
try:
statFolder = "/Users/chenwenguan/Downloads/2aab7e17-a1b6-1253/"
chartFolder = statFolder + "chart/"
if not os.path.exists(chartFolder):
os.mkdir(chartFolder)
filterData = []
readStatsFile(statFolder, filterData);
for dataItem in filterData:
percallList = map(lambda x: x["percall"], dataItem["cost"])
func = dataItem["func"]
line = dataItem["line"]
# 样本个数大于20才进行绘制
if len(percallList) > 20:
percallMean = numpy.mean(percallList) # 计算均值
# percallVar = numpy.var(percallMap) # 求方差
percallStd = numpy.std(percallList) # 计算标准差
# pvalue值大于0.05为正太分布
kstestResult = stats.kstest(percallList, 'norm', (percallMean, percallStd))
print "percallStd:%s, pvalue:%s" % (percallStd, kstestResult[1])
# 符合正态分布绘制分布曲线
if kstestResult[1] > 0.05:
threshold = percallMean + 3 * percallStd
drawGaussian(func, line, percallMean, threshold, percallList, chartFolder)
else:
drawCurve(func, line, percallList, chartFolder)
else:
pass
except Exception:
print 'exeption:' + traceback.format_exc()两种耗时模型绘制的曲线效果图如下:

函数耗时高斯分布曲线及阈值效果示例