1.简单介绍

卡方检验是一种用途很广的计数资料的假设检验方法。它属于非参数检验的范畴，主要是比较两个及两个以上样本率（构成比）以及两个分类变量的关联性分析。其根本思想就是在于比较理论频数和实际频数的吻合程度或拟合优度问题。
应用场景：两个率或两个构成比比较的卡方检验；多个率或多个构成比比较的卡方检验以及分类资料的相关分析等。
无效假设是：观察频数与期望频数没有差别。
卡方值的计算公式：

$x^2=\sum _{i=1}^n\frac{(O_i-E_i{)}^2}{E_i}$
O为观测频数，E为期望频数。

2.使用条件

2.1 随机样本数据

两个独立样本有以下情况：

• 所有的理论数T≥5并且总样本量n≥40，用Pearson卡方进行检验。
• 如果理论数T<5但T≥1，并且≥40，用连续性校正的卡方进行检验。
• 如果有理论数T<1或n<40,则用Fisher’s检验。

2.2 卡方检验的理论频数不能太小

对于R x C表：

• R×C表中理论数小于5的格子不能超过1/5;
• 不能有小于1的理论数。如果实验中有不符合R×C表的卡方检验，可以通过增加样本数、列合并来实现。

3.实现方法

3.1 关键函数

若要实现该方法，主要会用到scipy这个模块，关键函数为：scipy.stats.chi2_contingency

输入参数：

• observed：需要检验的R x C表，类型为array
• correction：修正参数，默认为True，若自由度为1，则应用Yates校正以获得连续性。修正的效果是将每个观测值向相应的期望值调整0.5。
• lambda_：默认情况下，此检验中计算的统计量是皮尔逊卡方统计量。可以设置为字符串或者数字。其他可选参数："pearson"(value 1);"log-likelihood"(value 0);"freeman-tukey"(value -1/2);"mod-log-likelihood"(value -1);"neyman"(value -2);"cressie-read"(value 2/3)。

输出：

• chi2: 检验统计量，即卡方值
• p: p-value，p值小于0.05则认为否定假设，即存在差异；若大于0.05则无法否定假设，两组差别无显著意义，简答来说就是，无差异
• dof ：自由度
• expected：基于表格的边际和，生成的期望频率或者期望值。

3.2例子

使用代码举例：

from scipy.stats import chi2_contingency
import numpy as np
kf_arr=np.array([[120,55],[80,25]])
kf= chi2_contingency(kf_arr)
##   chisq-statistic, p-value, expected_frep
kf

4.应用场景

4.1 独立性检验

假设要统计性别与选择高铁的座位类型是否有关，统计数据如下：

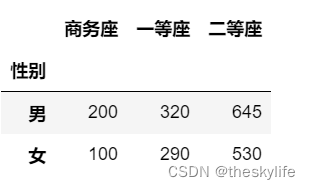
数据构建代码：

import pandas as pd
sex_seat_df=pd.DataFrame({'性别': ['男','女'],
             '商务座': [200,100],
             '一等座': [320,290],
             '二等座': [645,530]})
sex_seat_df.set_index('性别',inplace=True)

构建完成数据以后，可以利用scipy做卡方检验：

from scipy.stats import chi2_contingency
sex_seat_kf=chi2_contingency(sex_seat_df)
sex_seat_kf

卡方检验完成后，结果如下：

从以上的检测结果图，我们可以发现数据的卡方值为17.52,而p值为0.00<0.05，故我们认为原假设——“性别与选择高铁的座位类型无关” 不成立，即：性别与选择高铁的座位类型有关。
引申，那么卡方值为多少时，我们会认为性别与选择高铁的座位类型无关呢？
原数据的自由度为(3-1)*(2-1)=2，我们选择的置信水平为95%，将以下值代入，求得卡方的临界值，当原始数据的卡方值小于此数据时，我们认为是无关的：

import scipy
print(scipy.stats.chi2.ppf(0.95,2))

4.2 统一性检验

假设一家电影公司想要了解北京、上海和深圳三个城市对于新上市电影的喜好程度是否一致。现从以上城市各抽取800个消费者进行调查，喜好程度只能选择一项，调查结果如下：

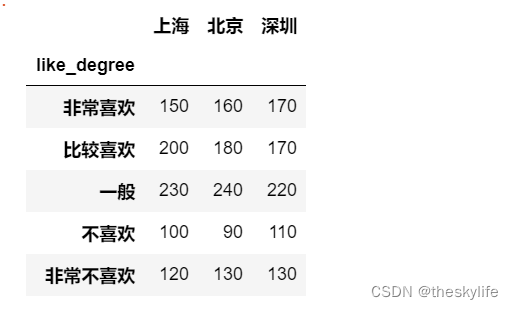
进行数据构建，并进行卡方检验：

import pandas as pd
from scipy.stats import chi2_contingency
movie_like_degree_city=pd.DataFrame({
    'like_degree':['非常喜欢','比较喜欢','一般','不喜欢','非常不喜欢'],
    '上海':[150,200,230,100,120],
    '北京':[160,180,240,90,130],
    '深圳':[170,170,220,110,130]
})
movie_like_degree_city.set_index("like_degree",inplace=True)
movie_kf=chi2_contingency(movie_like_degree_city)
print(movie_kf)

检验结果如下：

从以上数据可以看出，原数据的自由度为(5-1)*(3-1)=8，p-value为0.52>0.05，故没有理由拒绝原假设，原假设成立。即：北京、上海和深圳三个城市对于新上市电影的喜好程度相同。

4.3 适合度检验

假设我们要检验赌场的骰子是否动过手脚？可以对骰子进行一定数量的测试，并得出结果如下：

``
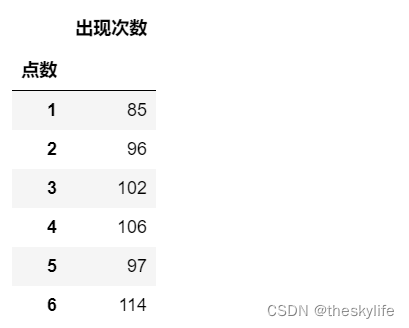
现在提出假设：骰子出现1-6的概率是一致的，进行卡方检验

# 统一性检验，检验骰子是否有问题
import numpy as np
from scipy import stats
#构建数据
observed_df=pd.DataFrame({'点数': [1, 2, 3, 4, 5, 6], '出现次数': [85, 96, 102, 106, 97, 114]})
observed_df.set_index('点数',inplace=True)
#现观察骰子出现情况
observed = observed_df.values
#期望频率
expected = np.array([100,100,100,100,100,100])
#计算卡方值和p-value
chi_v= np.sum(np.divide(np.square(observed-expected), expected))
#根据卡方值和自由度，计算p-value
p_value = 1 - stats.chi2.cdf(chi_v, len(observed)-1)
print(chi_v, p_value)

输出结果如下：

从以上结果可以发现，p值小于0.05，故拒绝原假设，即该骰子出现各个点数的概率是不一致的，存在问题。