Lecture3：神经网络与反向传播

news2024/11/19 11:24:08

1.计算图

2.反向传播与计算图

2.1 第一个例子

2.2 第二个例子--sigmoid

2.3 第三个例子--MAX门

2.4 第四和例子--对于向量的梯度

3.神经网络

4.常见矩阵求导公式

4.1 标量对向量求导

4.2 二次型对向量求导

1.计算图

在实践中我们想要推导和使用解析梯度，但是同时用数值梯度来检查我们的实现结果以确保我们的推导是正确的。

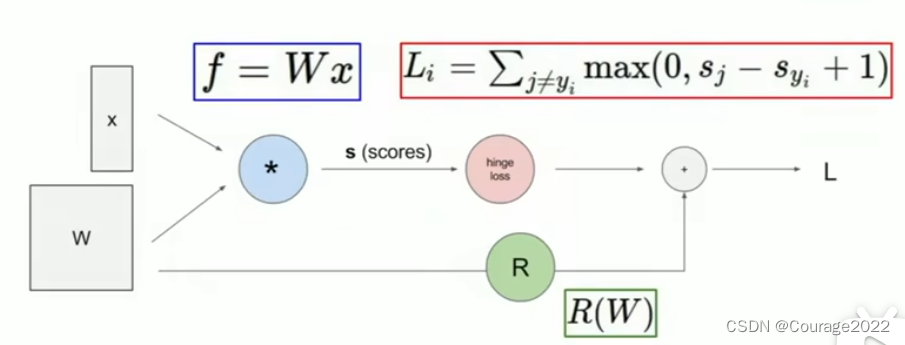
这篇博客将讲述如何计算任意复杂函数的解析梯度，需要利用到一个叫做计算图的框架。大体上来说，计算图就是我们用这类图表示任意函数，其中图的节点表示我们要执行的每一步计算，如下图的线性分类器：

一旦我们能用计算图表示一个函数，那么就能用反向传播技术递归地调用链式法则计算图中每个变量的梯度。

2.反向传播与计算图

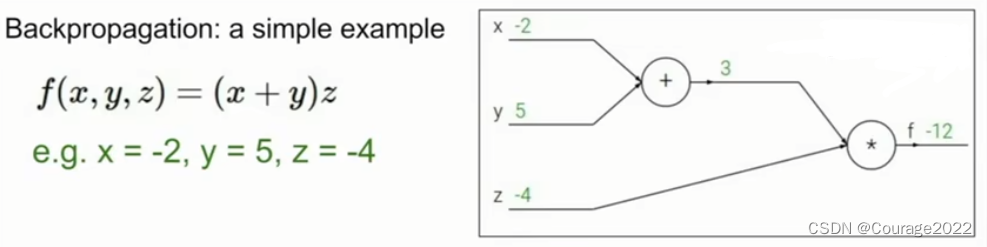
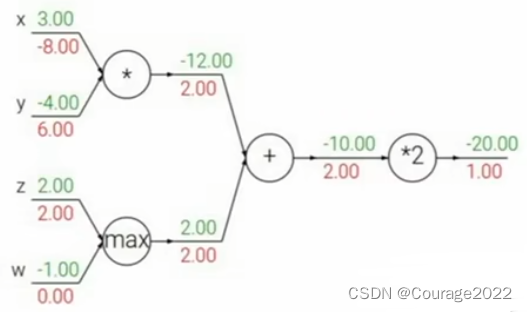
2.1 第一个例子

我们要找到函数输出对应任一变量的梯度。

第一步就是用计算图表示我们的整个函数，如上图中网络结构。

第二步是计算这个网络的前向传播，如上图中的绿色节点的值。

这里我们给每个中间变量一个名字：

$q=x+y \ \ ,\frac{\partial q}{\partial x}=1,\frac{\partial q}{\partial y}=1$

$f=qz \ \ ,\frac{\partial f}{\partial q}=z,\frac{\partial f}{\partial z}=q$

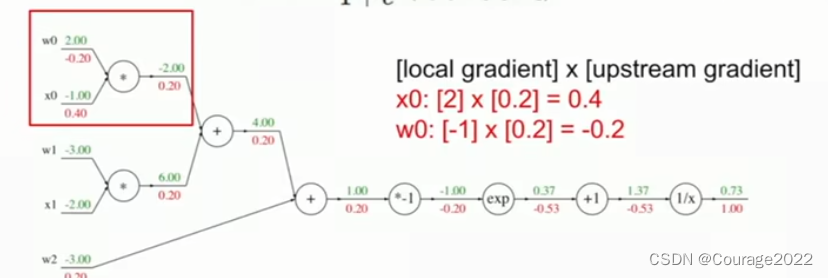
我们待求的变量是： $\frac{\partial f}{\partial x},\frac{\partial f}{\partial y},\frac{\partial f}{\partial z}$

我们可以用链式法则求： $\frac{\partial f}{\partial x}= \frac{\partial f}{\partial q}\frac{\partial q}{\partial x}=-4*1=-4$ ，其他两项也可以这么求。

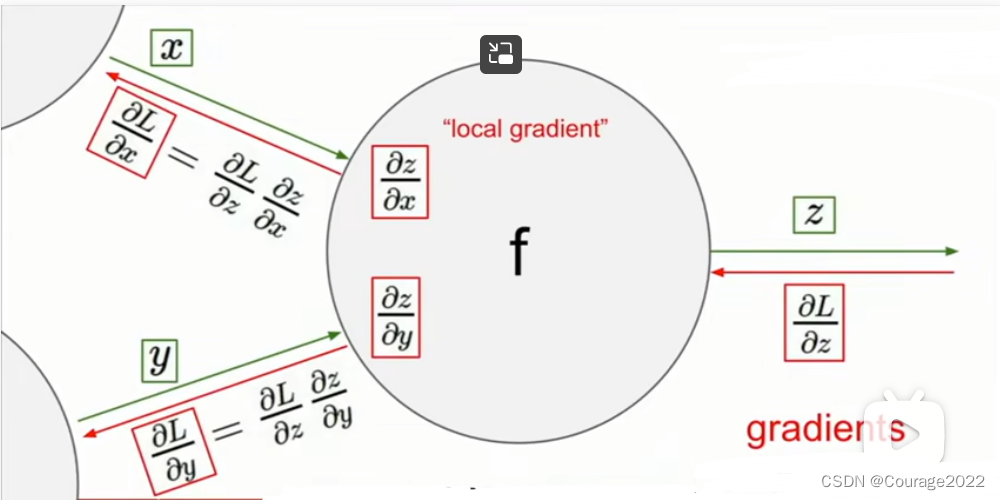
具体说来，在一个节点中，我们做了以下的事情：

①前向传播：根据输入 $x,y$ 计算输出 $z$

②根据它的表达式 $z=f(x,y)$ 来计算它的本地梯度 $\frac{\partial z}{\partial x},\frac{\partial z}{\partial y}$

③根据上层反向传播下来的对于此节点的梯度 $\frac{\partial L}{\partial z}$ 反向传播给上层节点 $\frac{\partial L}{\partial x},\frac{\partial L}{\partial y}$

2.2 第二个例子--sigmoid

$f(w,x)=\frac{1}{1+e^{-(w_{0}x_{0}+w_{1}x_{1}+w_{2})}}$

前向传播：

反向传播：

        因此，只要知道本地梯度与上层梯度，那么就能完成反向传播。

        我们也可以将一些节点组合在一起形成更复杂的节点，如下：

这么做的前提是能写出它的本地梯度才行，在这里我们定义了sigmoid函数：

$\sigma (x)=\frac{1}{1+e^{-x}}$

它的本地梯度为：

$\frac{d\sigma (x)}{dx}=(1-\sigma (x))\sigma (x)$

        通过这种方法我们还是可以完成反向传播。

2.3 第三个例子--MAX门

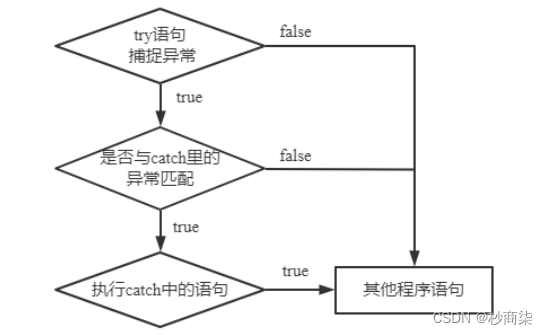
那么max门的梯度如何计算？在卷积神经网络的池化层中，最大池化卷积中的max梯度如何计算？

如上图，假设max门的上游梯度为2.0，那么这个本地梯度会是怎样的呢？

我们规定，其中一个变量将会得到刚传递回来的梯度完整值，另外一个变量会得到0。我们可以把这个想象成一个梯度路由器，加法节点回传相同的梯度给进来的两个分支，max门将获取梯度并且将其路由到它其中一个分支。因为只有最大值对应的值才会影响到后面。

2.4 第四和例子--对于向量的梯度

这里和前面没有什么区别，只是 $x,y,z$ 变成了向量的形式。

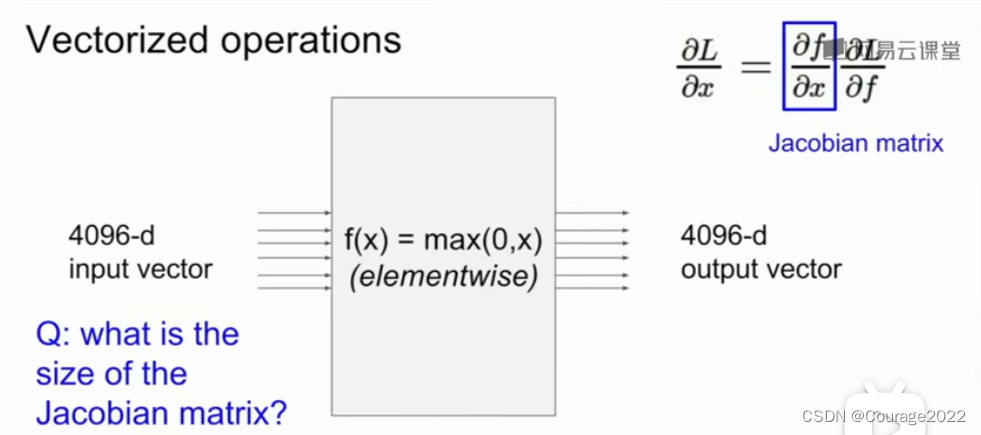
这时整个计算流程还是一样的，唯一的区别在于我们刚才的梯度变成了雅克比矩阵。所以现在是一个包含了每个变量里各元素导数的矩阵，比如 $z$ 在每个 $x$ 方向的导数。

        那么对于上面这个例子来说，雅可比矩阵的维度是多少呢？4096*4096。

        但在实际运算时多数情况下不需要计算这么大的雅克比矩阵，只需要算一个对角矩阵即可。
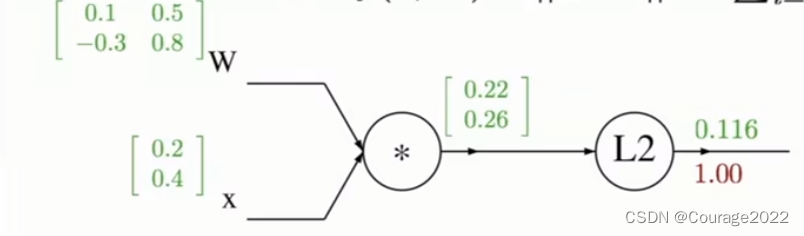
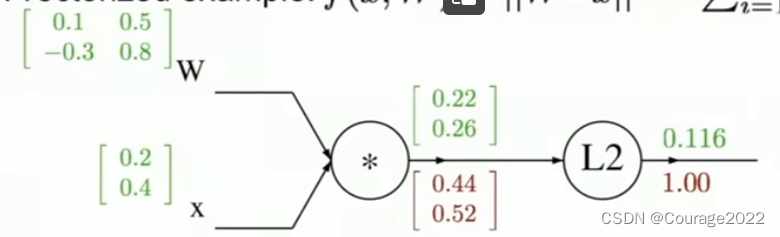
        我们举个具体的例子：

$f=(x,W)=||w\cdot x||^2=\sum_{i=1}^{n}(W\cdot x)_{i}^{2} \ \ \ x\epsilon \mathbb{R}^n,W\epsilon \mathbb{R}^{n\times n}$

类似如下：（我们实例化了这个例子）

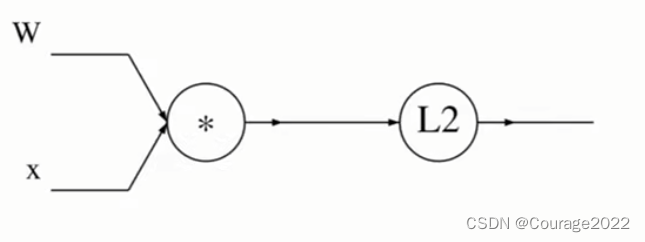
$q = W \cdot x = \begin{bmatrix} 0.1 & 0.5\\ -0.3 & 0.8 \end{bmatrix} \begin{bmatrix} 0.2\\ 0.4 \end{bmatrix}$

$f(q) = ||q||^2 = q_{1}^{2}+ q_{2}^{2}+ ...+ q_{n}^{2}$

   它的计算图如下：

和之前一样，首先将计算图写下来，如上。先将 $W$ 与 $x$ 相乘，再计算 $L_2$ 范数输出。

         现在我们来计算反向传播：

先计算 $q$ 方向上的梯度： $q$ 是一个二维向量，我们想要做到事情是找到 $q$ 的每个元素是怎样影响 $f$ 最终的值的，我们可以发现 $f$ 在特定 $q_i$ 中方向上的梯度是二倍的 $q_i$ ，即：

$\frac{\partial f}{\partial q_i}=2q_i$

如果写成向量的形式：

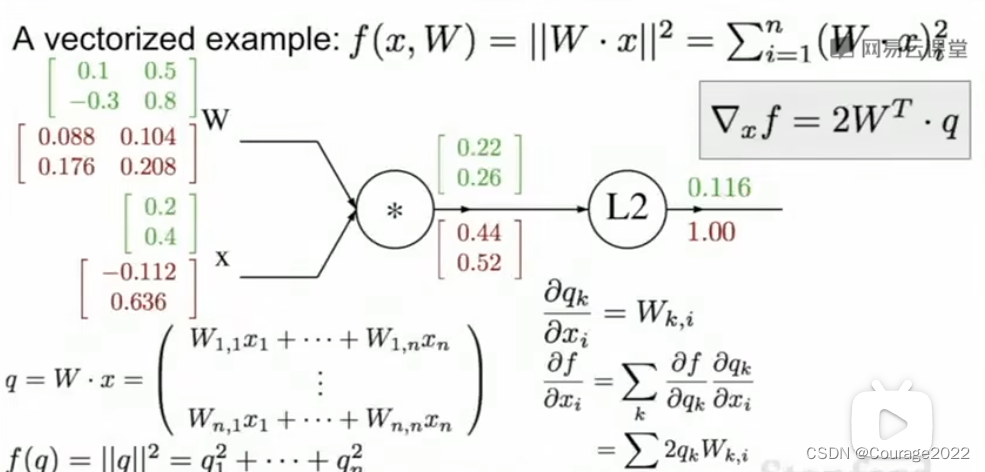
$\frac{\partial f}{\partial q} = \begin{bmatrix} 0.44\\ 0.52 \end{bmatrix}$

我们再来计算关于 $W$ 的梯度是什么：我们采用和之前相同的方法，使用链式法则，我们希望计算关于 $W$ 的 $q$ 的本地梯度，我们观察一下对每个 $q$ 的影响， $q$ 的每个元素对应 $W$ 的每个元素，这就是雅可比矩阵，那什么是导数呢？或者说 $q$ 的第一个元素的梯度是什么？我们的第一个元素对应 $W_{11}$ 所以 $q_1$ 对应 $W_{11}$ 么？

我们通过矩阵论的知识知道：

$\frac{\partial q_K}{\partial W_{i,j}}= 1_{k=i}x_j$

由此：

$\frac{\partial f}{\partial W_{i,j}}= \sum_{k}^{}\frac{\partial f}{\partial q_{k}}\frac{\partial q_{k}}{\partial W_{i,j}}=\sum_{k}^{}(2q_{k})(1_{k=i}x_j) =2q_ix_j$

同理：

$\frac{\partial f}{\partial x_{i}}= \sum_{k}^{}\frac{\partial f}{\partial q_{k}}\frac{\partial q_{k}}{\partial x_{i}}=2q_kW_{k,i}$

最后的结果如下：

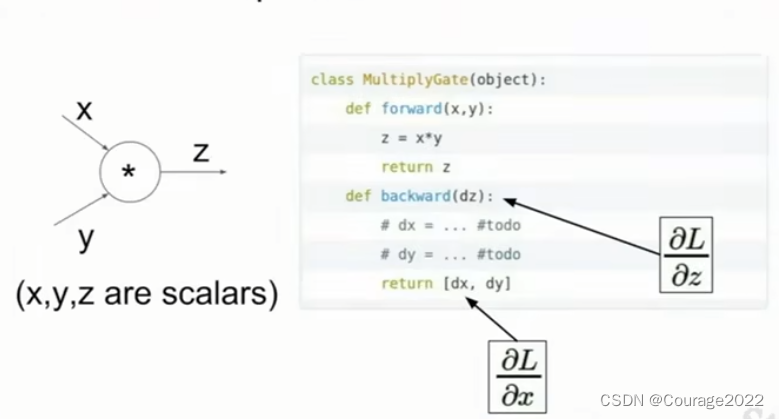
我们看一个偏导数门的运行，我们运行前向传播，输入 $x,y$ 输出 $z$ 。反向传播输入 $dz$ 逆向梯度希望输出的是 $\frac{ \partial L}{\partial x},\frac{ \partial L}{\partial y}$ 的梯度继续传递下去，我们需要注意的是我们需要缓存前向传播的数值，因为我们需要利用它取计算反向传播。因此在前向计算中我们需要缓存 $x,y$ 这些值，在反向计算使用链式法则将上游梯度的值使用其他分支的值对它进行量化并保持计算 $\frac{ \partial L}{\partial x},\frac{ \partial L}{\partial y}$ 。

3.神经网络

在我机器学习的专栏说过，这里不再赘述。

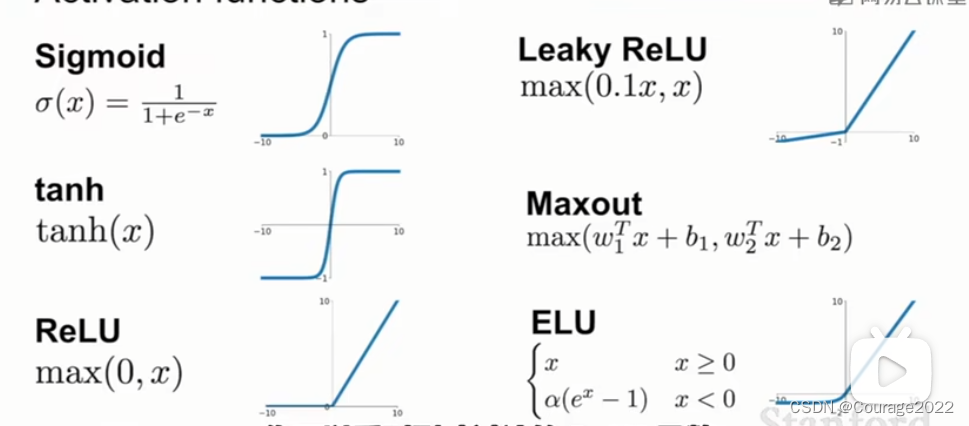
在这里放一个激活函数的预览图：

4.常见矩阵求导公式

4.1 标量对向量求导

已知：

$f(x)=A^T\cdot x=\sum_{i=1}^{n}a_ix_i,A=[a_1,a_2,...,a_n],x=[x_1,x_2,...,x_n]$ ，求 $\frac{df(x)}{dx}$ ：

$\frac{df(x)}{dx}=\begin{bmatrix} \frac{\partial f(x)}{\partial x_{1}}\\ \frac{\partial f(x)}{\partial x_{2}} \\ \frac{\partial f(x)}{\partial x_{3}} \\ ... \\ \frac{\partial f(x)}{\partial x_{n}} \end{bmatrix}=\begin{bmatrix} a_1\\ a_2 \\ a_3 \\ ... \\ a_n \end{bmatrix}$

因此：

$\frac{dA^Tx}{dx}=\frac{dx^TA}{dx}=A$

4.2 二次型对向量求导

已知： $f(x)=x^TAx=\sum_{i=1}^{n}\sum_{j=1}^{n}a_{ij}x_{i}x_{j},x\epsilon \mathbb{R}^n,A\epsilon \mathbb{R}^{n\times n}$ ，求 $\frac{df(x)}{dx}$ ：

$\frac{df(x)}{dx}=\begin{bmatrix} \frac{\partial f(x)}{\partial x_{1}}\\ \frac{\partial f(x)}{\partial x_{2}} \\ \frac{\partial f(x)}{\partial x_{3}} \\ ... \\ \frac{\partial f(x)}{\partial x_{n}} \end{bmatrix} =\begin{bmatrix} \sum_{j=1}^{n}a_{1j}x_{j}+\sum_{i=1}^{n}a_{i1}x_{i}\\ \sum_{j=2}^{n}a_{1j}x_{j}+\sum_{i=1}^{n}a_{i2}x_{i} \\ \sum_{j=3}^{n}a_{1j}x_{j}+\sum_{i=1}^{n}a_{i3}x_{i} \\ ... \\ \sum_{j=n}^{n}a_{1j}x_{j}+\sum_{i=1}^{n}a_{in}x_{i} \end{bmatrix}$

因此：

$\frac{df(x)}{dx} = Ax + A^Tx$