点击跳转专栏=>Unity3D特效百例
点击跳转专栏=>案例项目实战源码
点击跳转专栏=>游戏脚本-辅助自动化
点击跳转专栏=>Android控件全解手册
点击跳转专栏=>Scratch编程案例
点击跳转=>软考全系列
点击跳转=>蓝桥系列

👉关于作者

专注于Android/Unity和各种游戏开发技巧，以及各种资源分享（网站、工具、素材、源码、游戏等）
有什么需要欢迎底部卡片私我，获取更多支持，交流让学习不再孤单。

芝麻粒儿-空名先生

👉实践过程

需要所有整理的文档可底部卡片联系我，直接发压缩包。

😜连号区间数

标题：连号区间数
小明这些天一直在思考这样一个奇怪而有趣的问题：
在1~N的某个全排列中有多少个连号区间呢？这里所说的连号区间的定义是：
如果区间[L, R] 里的所有元素（即此排列的第L个到第R个元素）递增排序后能得到一个长度为R-L+1的“连续”数列，
则称这个区间连号区间。
当N很小的时候，小明可以很快地算出答案，但是当N变大的时候，问题就不是那么简单了，现在小明需要你的帮助。

输入格式：
第一行是一个正整数N (1 <= N <= 50000), 表示全排列的规模。
第二行是N个不同的数字Pi(1 <= Pi <= N)，表示这N个数字的某一全排列。

输出格式：
输出一个整数，表示不同连号区间的数目。

示例：
用户输入：
4
3 2 4 1

程序应输出：
7

用户输入：
5
3 4 2 5 1

程序应输出：
9

解释：
第一个用例中，有7个连号区间分别是：[1,1], [1,2], [1,3], [1,4], [2,2], [3,3], [4,4]
第二个用例中，有9个连号区间分别是：[1,1], [1,2], [1,3], [1,4], [1,5], [2,2], [3,3], [4,4], [5,5]

//c++
#include <iostream>

using namespace std;

int n;
int arr[50000];
int ans;

int main(int argc, const char *argv[]) {
    scanf("%d", &n);
    for (int i = 0; i < n; ++i) {
        scanf("%d", &arr[i]);
    }
    for (int j = 0; j <= n - 1; ++j) {
        int min=arr[j];
        int max = arr[j];
        for (int i = j; i <= n - 1; ++i) {
            if(arr[i]>max)
                max=arr[i];
            if(arr[i]<min)
                min=arr[i];
            if (i == j)
                ans++;
            else {
                 if(max-min+1==i-j+1)
                     ans++;//j-i形成连号区间
            }
        }
    }
    printf("%d\n",ans);
    return 0;
}

//java
import java.util.Scanner;

public class _10连号区间数 {
  public static void main(String[] args) {
    Scanner sc = new Scanner(System.in);
    int n = sc.nextInt();
    int[] arr = new int[n+1];
    for (int i = 1; i <=n ; i++) {
      arr[i]=sc.nextInt();
    }
    int ans=0;
    for (int i = 1; i <=n ; i++) {
      int max=arr[i];
      int min=arr[i];
      for (int j = i; j <=n ; j++) {//]的位置
        if (arr[j]>max)max=arr[j];
        if (arr[j]<min)min=arr[j];
        if (i==j){
          // System.out.printf("[%d,%d]\n",i,j);
          ans++;
        }
        else{//i<j,怎么判断[i,j]是连号区间呢？
          if (max-min==j-i){
            // System.out.printf("[%d,%d]\n",i,j);
            ans++;
          }

        }
      }
    }
    System.out.println(ans);
  }
}

😜剪格子

标题：剪格子
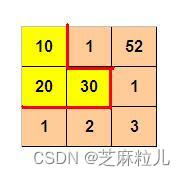
在这里插入图片描述

如图所示，3 x 3 的格子中填写了一些整数。
我们沿着图中的红色线剪开，得到两个部分，每个部分的数字和都是60。
本题的要求就是请你编程判定：对给定的m x n 的格子中的整数，是否可以分割为两个部分，使得这两个区域的数字和相等。
如果存在多种解答，请输出包含左上角格子的那个区域包含的格子的最小数目。
如果无法分割，则输出 0

程序输入输出格式要求：
程序先读入两个整数 m n 用空格分割 (m,n<10)
表示表格的宽度和高度
接下来是n行，每行m个正整数，用空格分开。每个整数不大于10000
程序输出：在所有解中，包含左上角的分割区可能包含的最小的格子数目。

例如：
用户输入：
3 3
10 1 52
20 30 1
1 2 3
则程序输出：
3

再例如：
用户输入：
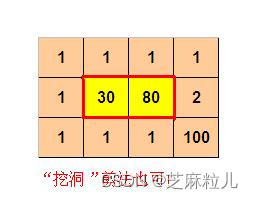
4 3
1 1 1 1
1 30 80 2
1 1 1 100
则程序输出：
10
在这里插入图片描述

#include <iostream>
#include <algorithm>
#include <queue>
#include <set>
#define mk(i,j) make_pair(i,j)
using namespace std;

int m, n;
int total;
int g[10][10];
int ans;
/*抽象了一种剪辑方法*/
class Cut {
public:
    set<pair<int, int> > grids;//包含若干格子
    int sum;//所有格子的数值的求和
};
/**
 * 将st中的元素拷贝到新set中
 * @param st
 * @return
 */
set<pair<int, int> > copySet(set<pair<int, int> > &st) {
    set<pair<int, int> >::iterator iter = st.begin();
    set<pair<int, int> > ans;
    while (iter != st.end()) {
//        重新mkpair，加入新set中
        ans.insert(*iter);
        iter++;
    }
    return ans;
}
void add(int sum, int i, int j, set<pair<int, int> > &grids, Cut *&cut_new) {
    const pair<int, int> &pair_n = make_pair(i , j);
//                    深度拷贝set
    set<pair<int, int> > grids_copy=copySet(grids);
    grids_copy.insert(pair_n);
    cut_new->grids=grids_copy;
    cut_new->sum=sum+g[i][j];
}
vector<Cut *> vs[100];//分别存储格子数为1~100的各种剪法

int main(int argc, const char *argv[]) {
    scanf("%d %d", &m, &n);
    for (int i = 0; i < n; ++i) {
        for (int j = 0; j < m; ++j) {
            scanf("%d", &g[i][j]);
            total += g[i][j];
        }
    }
//    第一个格子就是一半
    if (g[0][0] == total / 2) {
        printf("%d\n", 1);
        return 0;
    }

    /*左上角格子,只有一种剪法，加入v[1]*/
    Cut *c = new Cut();
    const pair<int, int> p = make_pair(0, 0);
    c->grids.insert(p);
    c->sum = g[0][0];
    vs[1].push_back(c);//只包含一个格子且包含00的只有一种剪法

    for (int i = 2; i <= m * n; ++i) {
//        i是格子数，用vs[i-1]里面的来生成
//迭代vs[i-1]里面的所有剪法
        for (int j = 0; j < vs[i - 1].size(); ++j) {
//            pCut代表一种剪辑方法
            Cut *pCut = vs[i - 1][j];
//            这种剪辑方法里面记录了所有格子，这些格子每个都扩展一个，即形成个数+1的剪法
            set<pair<int, int> > &grids = pCut->grids;
            int sum = pCut->sum;
            set<pair<int, int> >::iterator iter = grids.begin();
//            迭代所有的格子，尝试添加它的邻居
            while (iter != grids.end()) {
                const pair<int, int> &p = *iter;//代表一个格子的坐标
                int x=p.first;
                int y=p.second;

                if(x+1<n&&grids.find(mk(x+1,y))==grids.end()){//下方，能走通且下方格子不在当前集合中

                    Cut *cut_new=new Cut();//生成一个新的剪法
                    add(sum, x+1, y, grids, cut_new);//将原有的格子全部拷入，再增加当前试探的新的格子
                    if(cut_new->sum==total/2){
                        printf("%d\n", i);
                        return 0;
                    }else if(cut_new->sum<total/2)
                        vs[i].push_back(cut_new);
                }
                if(x-1>=0&&grids.find(mk(x-1,y))==grids.end()){//上方
                    Cut *cut_new=new Cut();
                    add(sum, x-1, y, grids, cut_new);
                    if(cut_new->sum==total/2){
                        printf("%d\n", i);
                        return 0;
                    }else if(cut_new->sum<total/2)
                    vs[i].push_back(cut_new);
                }
                if(y+1<m&&grids.find(mk(x,y+1))==grids.end()){//右方
                    Cut *cut_new=new Cut();
                    add(sum, x, y+1, grids, cut_new);
                    if(cut_new->sum==total/2){
                        printf("%d\n", i);
                        return 0;
                    } else if(cut_new->sum<total/2)
                    vs[i].push_back(cut_new);
                }
                if(y-1>=0&&grids.find(mk(x,y-1))==grids.end()){//左方
                    Cut *cut_new=new Cut();
                    add(sum, x, y-1, grids, cut_new);
                    if(cut_new->sum==total/2){
                        printf("%d\n", i);
                        return 0;
                    }else if(cut_new->sum<total/2)
                    vs[i].push_back(cut_new);
                }
                iter++;
            }
        }
    }
    printf("%d\n", 0);
    return 0;
}

😜买不到的数目

标题：买不到的数目
小明开了一家糖果店。他别出心裁：把水果糖包成4颗一包和7颗一包的两种。糖果不能拆包卖。
小朋友来买糖的时候，他就用这两种包装来组合。当然有些糖果数目是无法组合出来的，比如要买 10 颗糖。
你可以用计算机测试一下，在这种包装情况下，最大不能买到的数量是17。大于17的任何数字都可以用4和7组合出来。
本题的要求就是在已知两个包装的数量时，求最大不能组合出的数字。

输入：
两个正整数，表示每种包装中糖的颗数(都不多于1000)

要求输出：
一个正整数，表示最大不能买到的糖数

不需要考虑无解的情况

例如：
用户输入：
4 7
程序应该输出：
17

再例如：
用户输入：
3 5
程序应该输出：
7

#include <iostream>
#include <set>

using namespace std;

int main(int argc, const char *argv[]) {
    int a, b;
    scanf("%d %d", &a, &b);
    set<int> ss;
//    枚举a*x+b*y的值，上边界是a*b
    for (int x = 0; a * x <= a * b; ++x) {
        for (int y = 0; a * x + b * y <= a * b; ++y) {
            ss.insert(ss.end(), a * x + b * y);
        }
    }
    for (int i = a * b; i >= 0; --i) {
        if (ss.find(i) == ss.end())//i不在set中，那么i就是答案
        {
            printf("%d\n", i);
            break;
        }
    }
    return 0;
}

😜翻硬币

题目标题：翻硬币
小明正在玩一个“翻硬币”的游戏。
桌上放着排成一排的若干硬币。我们用 * 表示正面，用 o 表示反面（是小写字母，不是零）。
比如，可能情形是：oooooo
如果同时翻转左边的两个硬币，则变为：oooo**oooo
现在小明的问题是：如果已知了初始状态和要达到的目标状态，每次只能同时翻转相邻的两个硬币,那么对特定的局面，
最少要翻动多少次呢？
我们约定：把翻动相邻的两个硬币叫做一步操作，那么要求：

程序输入：
两行等长的字符串，分别表示初始状态和要达到的目标状态。每行的长度<1000

程序输出：
一个整数，表示最小操作步数

例如：
用户输入：

程序应该输出：
5

再例如：
用户输入：
ooo***
ooo***

程序应该输出：
1

//c++
#include <iostream>
#include <queue>
#include <set>

using namespace std;

typedef struct stateAndLevel {
    string str;
    int level;
} stateAndLevel;

queue<stateAndLevel> queue1;
set<string> set1;
int n;

int main(int argc, const char *argv[]) {
    string src;
    string target;
    getline(cin, src);
    getline(cin, target);
    n = src.length();
    stateAndLevel first = {src, 0};
    queue1.push(first);//队列的第一个元素就是原串

    while (!queue1.empty()) {
        //获取并弹出队列首部
        stateAndLevel &front = queue1.front();
        queue1.pop();

        string basicString = front.str;
//        如果队首元素和目标一致，可以终止程序
        if (basicString.compare(target) == 0) {
            cout << front.level << endl;//输出层次，也就是变化多少次到达了这个状态
            return 0;
        }
//        把已经处理过的字符串加入set中备查，避免往回翻的状态重复加入
        set1.insert(basicString);
//        模拟，依次翻转后加入队列中
        for (int i = 0; i < n - 1; ++i) {
            string buff;
            buff.insert(0, basicString);
//            拷贝之后，翻转i和i+1两个位置的字符
            if (buff[i] == '*')
                buff[i] = 'o';
            else
                buff[i] = '*';
            if (buff[i + 1] == 'o')
                buff[i + 1] = '*';
            else
                buff[i + 1] = 'o';
//            string s(buff);//字符数组转字符串
            if (set1.find(buff) == set1.end()) {
                stateAndLevel obj = {buff, front.level + 1};
                queue1.push(obj);
            }
        }
//        cout << queue1.size() << endl;
    }

//    cout << src << "\n" << target << endl;
    return 0;
}

//c++
#include <iostream>
#include <queue>
#include <set>

using namespace std;

int main(int argc, const char *argv[]) {
    string src;
    string target;
    getline(cin, src);
    getline(cin, target);
    int n = src.length();
    int ans=0;
    int start=-1;
    for (int i = 0; i < n; ++i) {
        if(src[i]!=target[i]){
            if(start==-1)//还没标记第一个位置
            {
                start=i;
            }else//第一个位置已经标记,现在已经找到了第二个位置
            {
                ans+=(i-start);
                start=-1;
            }
        }
    }
    cout<<ans<<endl;
    return 0;
}

👉其他

📢作者：小空和小芝中的小空
📢转载说明-务必注明来源：https://zhima.blog.csdn.net/
📢这位道友请留步☁️，我观你气度不凡，谈吐间隐隐有王者霸气💚，日后定有一番大作为📝！！！旁边有点赞👍收藏🌟今日传你，点了吧，未来你成功☀️，我分文不取，若不成功⚡️，也好回来找我。

温馨提示：点击下方卡片获取更多意想不到的资源。
空名先生