题目链接:AcWing 98. 分形之城
问题描述

分析
这一道题看起来很麻烦，其实就是比较麻烦。
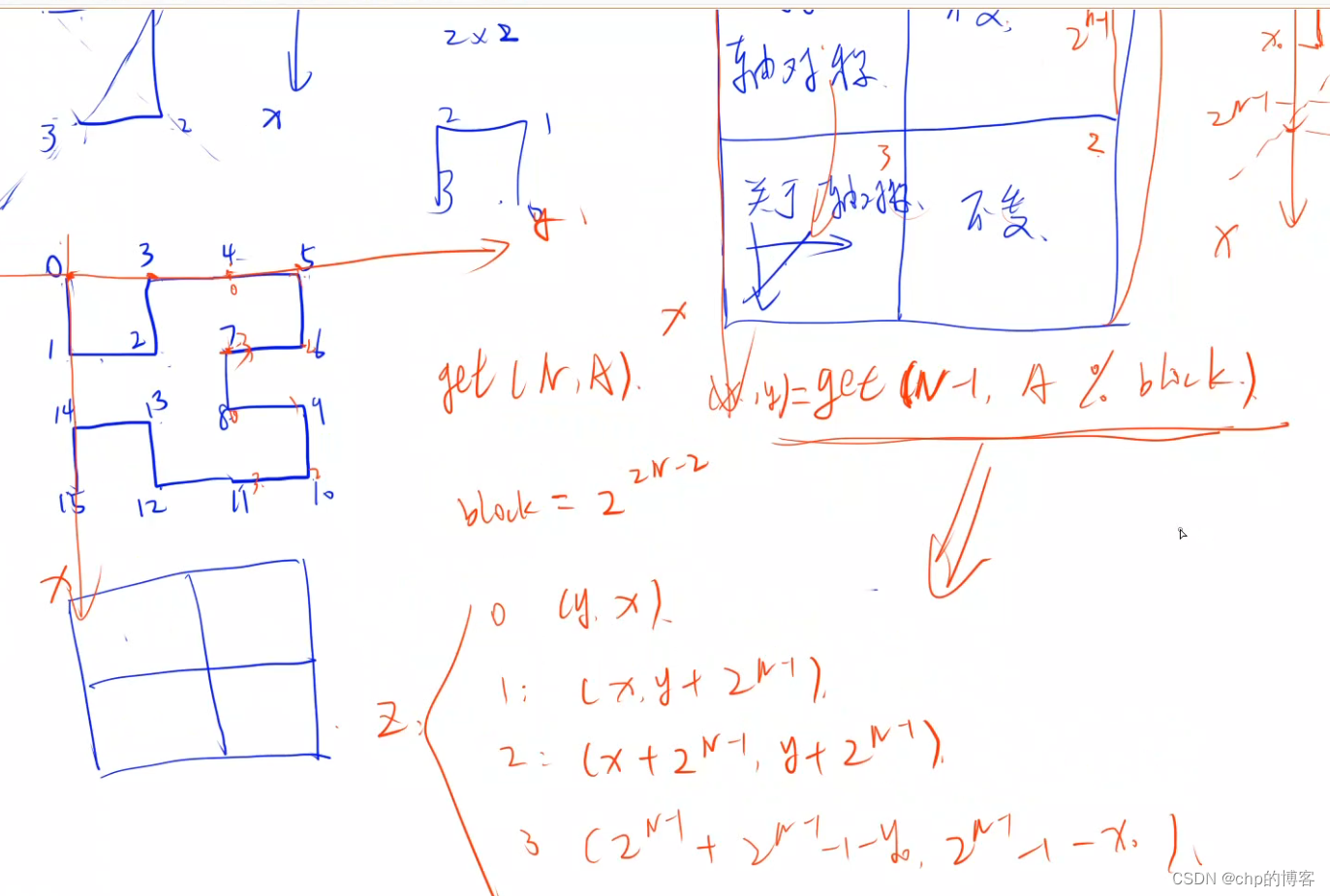
这是一道递归+坐标变换的问题，坐标变换比较难想，建议自己动手画一画容易明白一些。
首先是城市等级 $n$ 与总点数的关系，不难发现总点数 $=2^{2\ast n}$，同时可以发现，每个等级由$4$个等级为$n-1$的城市构成，将每个等级为$n-1$的城市表示为 $block$ 每个 $block$ 的点数为 $=2^{2\ast (n-1)}=2^{2\ast n-2}$个，观察可以发现城市由 $block$ 构成的规律，第1部分是关于 $y=x对称$ ，第2部分是与 $block$相同，第3部分是与 $block$相同，第4部分是关于 $y=2^{n-1}-x对称$
分别考虑当前点在城市的$4$个区域的情况递归子问题即可

代码如下:

#include<cstdio>
#include<algorithm>
#include<iostream>
#include<cstring>
#include<cmath>
using namespace std;
typedef long long ll;
struct node{
    ll x,y;
};
node get(ll n,ll a){
    if(n==0) return {0,0};
    ll block=1ll<<(2*n-2);
    ll len=1ll<<(n-1);
    node b=get(n-1,a%block);
    ll x=b.x,y=b.y;
    if(a/block==0) return {y,x};
    if(a/block==1) return {x,y+len};
    if(a/block==2) return {x+len,y+len};
    if(a/block==3) return {2*len-1-y,len-1-x};
}
int main(){
    int t;
    cin>>t;
    while(t--){
        ll n,a,b;
        cin>>n>>a>>b;
        node pa=get(n,a-1);
        node pb=get(n,b-1);
        ll dx=pa.x-pb.x;
        ll dy=pa.y-pb.y;
        // cout<<dx<<" "<<dy<<endl;
        printf("%.0lf\n",sqrt(dx*dx+dy*dy)*10);
    }
    return 0;
}