题目：
一道Google真实出现过的面试题
将一段纸条放在桌上，然后从纸条下边向上方对折1次，压出折痕后展开，此时折痕是凹下去的（称为凹折痕），即折痕凸起的方向指向纸条的背面。如果从纸条的下边向上方连续对折两次，压出折痕后展开，此时有三条折痕，从上到下依次是（凹折痕 -> 凹折痕 -> 凸折痕）。
给定一个参数N，代表纸条从下向上连续对折N次。从上到下打印所有折痕的方向。
例如：N = 1 时，打印：down（代表凹折痕），N = 2时，打印 down down up（凹 -> 凹 -> 凸）
经过三次对折后的纸条，标记出来每次折之后的凹凸折痕。经过观察会发现，第三次对折之后，在原有的2折痕基础上，对称的出现了3的凹凸折痕，所以，有理由可以相信，第四次对折后，会在3折痕的基础上对称的出现凹凸折痕。

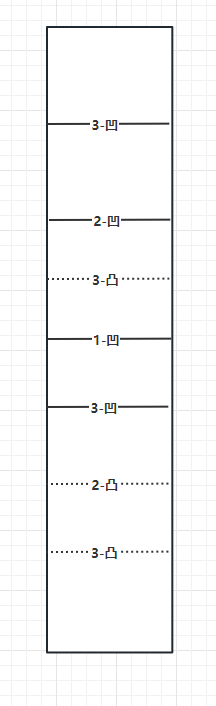
那如果按照题目进行从上到下的打印凹凸折痕，将整个纸条想象成一颗二叉树，那么，是不是就是二叉树的中序遍历！！

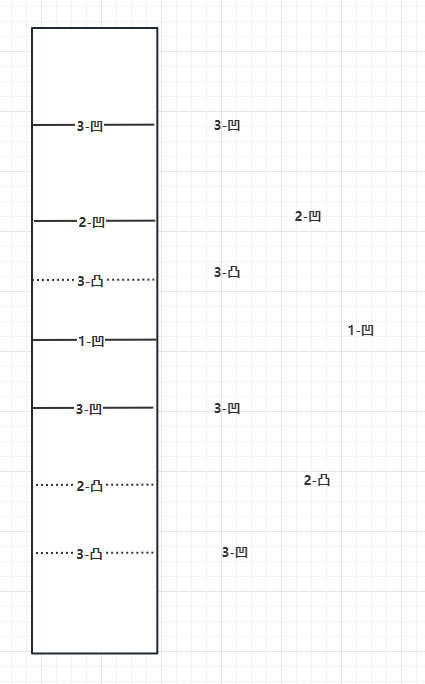
并且这棵二叉树，是一个有规律的二叉树

1. 头节点是凹的
2. 所有左子树的头是凹的
3. 所有右子树的头的凸的

public static void printAllFolds(int N) {
        process(1, N, true);
    }

    //将其整个打印过程想象成一颗二叉树
    //当前你来到了第i层
    //共有N层（对折了N次）
    //因为二叉树有规律，head节点是 凹的，所以上来默认 down = true
    //所有的左侧头结点是凹的 down = T
    //所有的右侧头结点是凸的 down = F
    //如果第 i 层 > 实际对折次数，return
    public static void process(int i, int N, boolean down) {
        if (i > N) {
            return;
        }

        process(i + 1, N, true);
        System.out.print(down ? " 凹 " : " 凸 ");
        process(i + 1, N, false);
    }