149. 直线上最多的点数（困难）

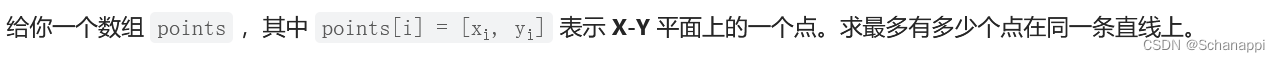
枚举直线 + 哈希表统计

思路

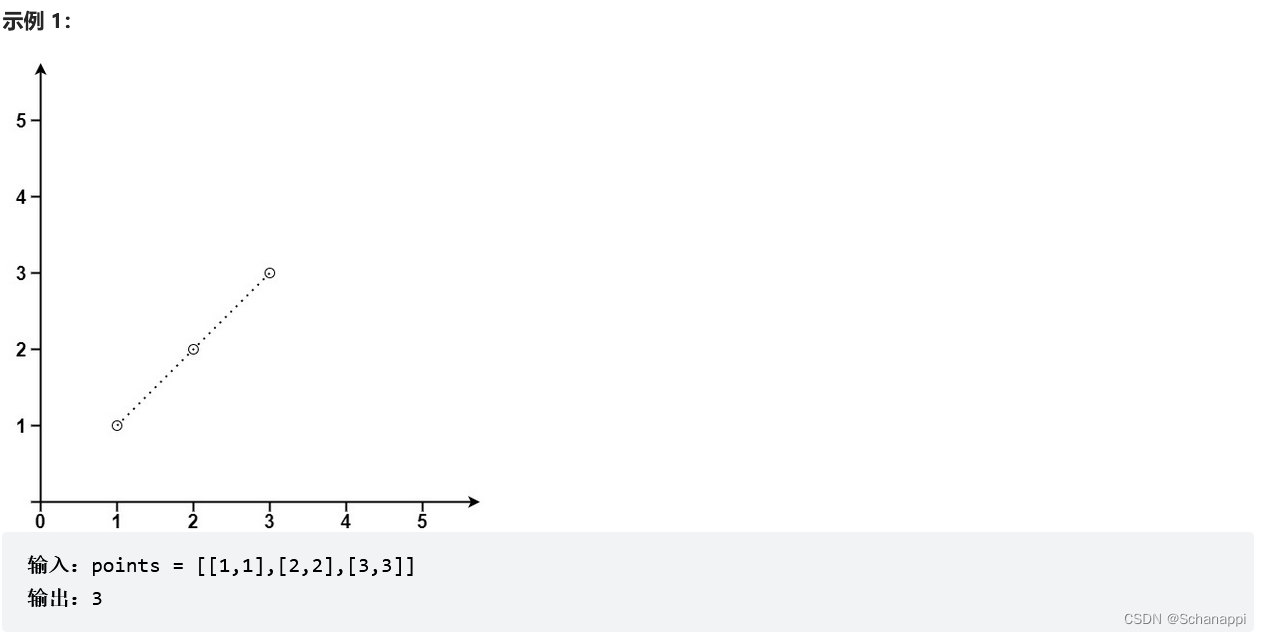
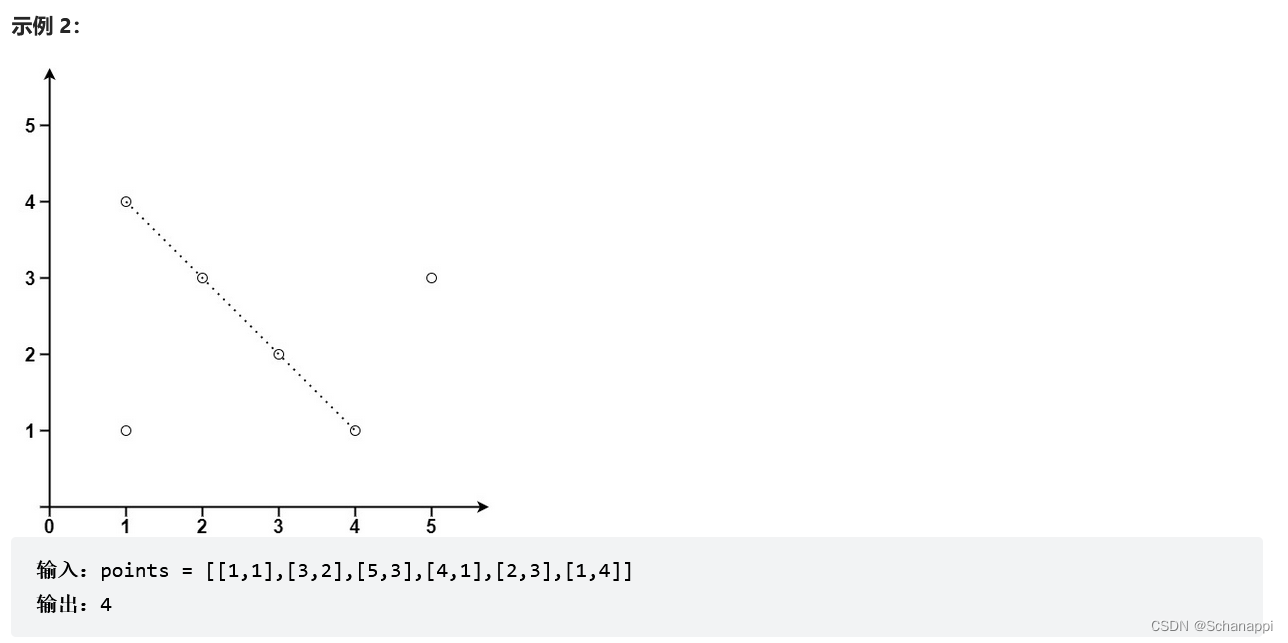
• 遍历每两个点之间的连线，然后计算这条连线上有多少个点。
  具体步骤如下：

  1. 初始化最大点数为 0。
  2. 遍历每个点，用它和其他点计算斜率。
  3. 如果两个点的x坐标相同，斜率设为INT_MAX；否则，计算斜率，即两个点的y 差值除以 x 差值。
  4. 使用一个哈希表mp来记录每个斜率对应的点的个数，初始值为2（两个点）。
  5. 遍历其他点，如果它们和当前点的斜率相同，则将对应斜率的点数加1。
  6. 更新最大点数为mp中的最大值。
  7. 返回最大点数。

• 为了避免重复计算，使用一个 flag 数组来标记已经处理过的点。在内层循环中，如果一个点已经被标记过，则直接跳过。

• 这个思路的时间复杂度为O(n²)，因为需要两重循环来遍历所有的点对。

• 缺点：在每次遍历点集之前都创建了一个新的 flag 数组和 mp 哈希表，这样会导致重复的计算。

易错点

1. 错误处理斜率不存在（即两个点横坐标相同）的情况，将 k 标记为 0；
2. 斜率可能为浮点数，一开始也标记为 int ；
3. 一开始将 flag 数组 和 mp 哈希表放在大循环外边，导致有些点没有计算到。

代码

class Solution {
public:
    int maxPoints(vector<vector<int>>& points) {
        int n = points.size();
        if(n < 3)   return n;
        int maxPoint = 0;
        
        for(int i=0; i<n-1; ++i){
            vector<int> flag(n, 0);
            unordered_map<double, int> mp;
            if(flag[i]) continue;
            flag[i] = 1;
            for(int j=i+1; j<n; ++j){
                if(flag[j]) continue;
                flag[j] = 1;
                double k;
                // 斜率=0
                if(points[j][0] == points[i][0]) k = INT_MAX;
                else k = (double)(points[j][1] - points[i][1]) / (double)(points[j][0] - points[i][0]);
                mp[k] += 2;
                for(int p=j+1; p<n; ++p){
                    if(flag[p]) continue;
                    // 在同一条直线上
                    if(points[p][0] == points[j][0] && k == INT_MAX){
                        flag[p] = 1;
                        mp[k] ++;
                    }
                    if(((double)(points[p][1] - points[j][1]) / (double)(points[p][0] - points[j][0])) == k){
                        flag[p] = 1;
                        mp[k] ++;
                    }
                }
            }
            for(auto key : mp){
                maxPoint = max(maxPoint, key.second);
            }
        }

        return maxPoint;
    }
};