【动态规划算法】第四题：91.解码方法

news2024/10/5 16:31:28

💖作者：小树苗渴望变成参天大树
🎉作者宣言：认真写好每一篇博客
🎊作者gitee:gitee
💞作者专栏：C语言,数据结构初阶,Linux,C++ 动态规划算法

如果你喜欢作者的文章，就给作者点点关注吧！

文章目录

前言

前言

今天我们开始讲解动态规划的第四题，博主认为再理解方面比第三题简单，但是代码方便些起来比前面的细节更多一些，因为初始化和前面的有所差别，最后再讲解一下优化问题，我们开始进入正文

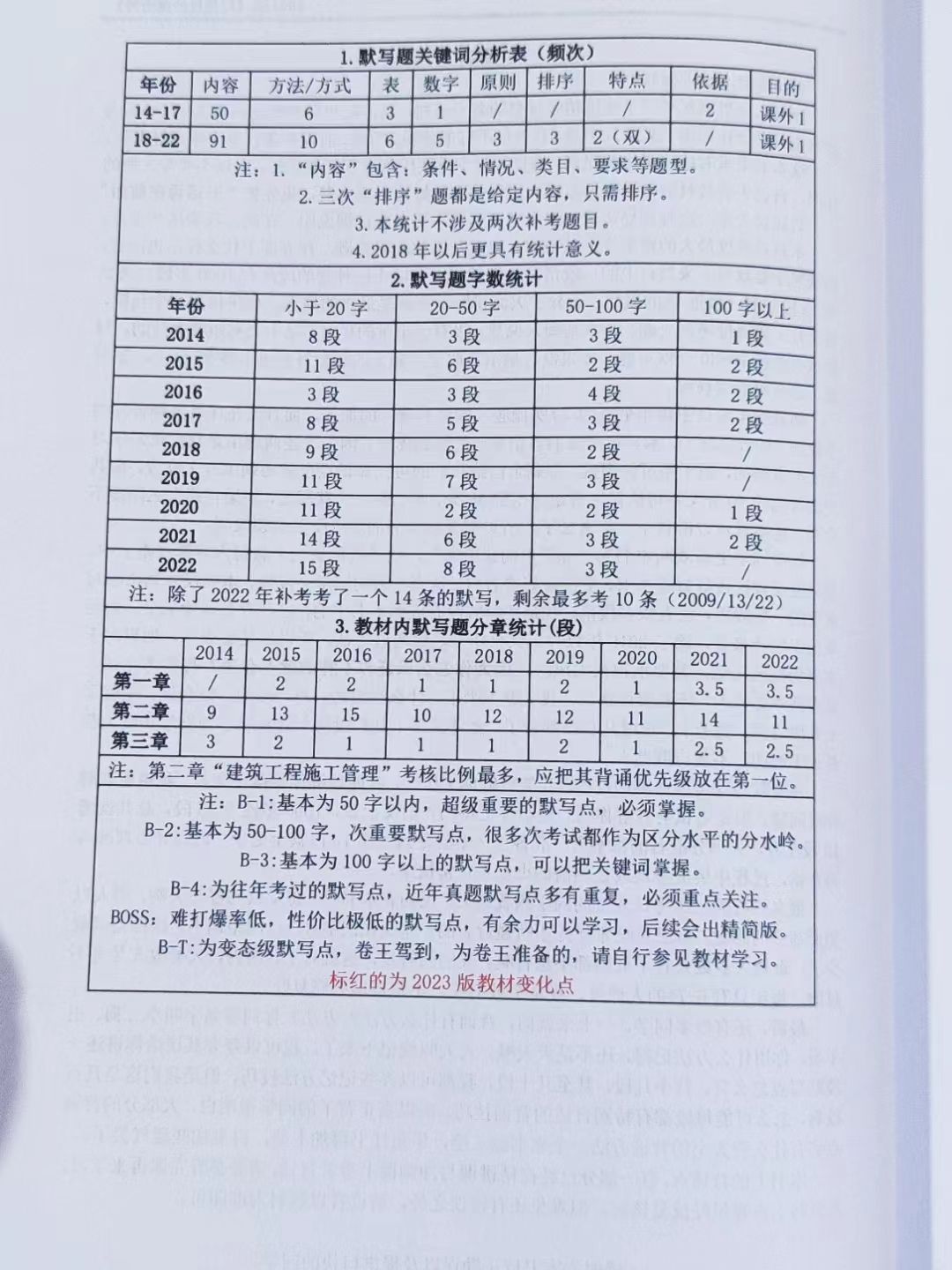
第四个题目是解码方法
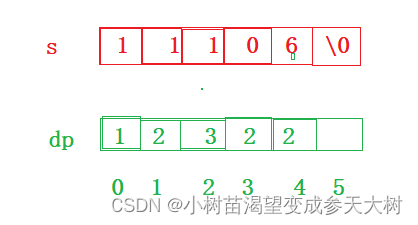
在这里插入图片描述
我们来看图解解析：

对于题解，题目说的非常清楚了，有具体案例，上面图解讲解了特性，一会些状态转移方程需要用到

通过动态规划的五个步骤解题：

状态表示：经验+题目要求：以i位置为结尾，dp[i]表示：当字符串有i个的时候，dp[i]为可以解码的总数
状态转移方程
根据题目要求，以i位置为结尾，最近的状态来分析

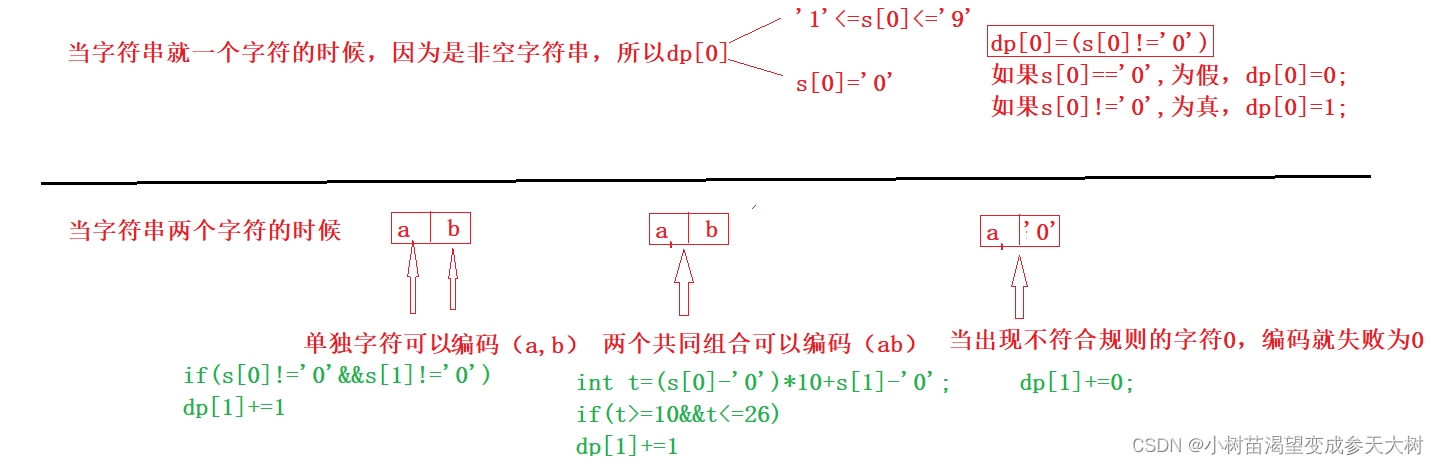
当s[i] 上的数在 [1, 9] 区间上时： dp[i] += dp[i - 1] ；
当s[i - 1] 与s[i] 上的数结合后，在[10, 26] 之间的时候： dp[i] +=
dp[i - 2]

初始化：保证数组不越界出现i-1，i-2，将dp[0],dp[1]初始化即可
填表顺序：从左往右
返回值：根据题目要求,根据伊卡斯hi的图解，字符串后面还有一个\0,大小为n,实际有效字符有n个，所以dp[n-1]才是返回解码总数

代码实现：

class Solution {
public:
    int numDecodings(string s) {
            //1.创建dp表
            //2.初始化
            //3.填表
            //4.返回值
            int n=s.size();
            vector<int> dp(n);
            dp[0]=s[0]!='0';//非空字符串
            if(n==1)return dp[0];

            if(s[0]!='0'&&s[1]!='0')dp[1]+=1;//单独解码初始化
            int t=(s[0]-'0')*10+s[1]-'0';
            if(t>=10&&t<=26)dp[1]+=1;//两个组合解码初始化

            for(int i=2;i<n;i++)
            {
            	//两者各自成功的时候+1,分开算。失败的时候就不用算进来了。
                if(s[i]!='0')dp[i]+=dp[i-1];
                int t=(s[i-1]-'0')*10+s[i]-'0';
                if(t>=10&&t<=26)dp[i]+=dp[i-2];
            }
            return dp[n-1];
     }
 }

优化： 大家应该发现我们的初始化和循环里面的代码几乎一样，那我们怎么解决这样的问题呢？？我们就要再初始化上做动作:

在这里插入图片描述

这种方法也叫处理边界及初始化问题:这题不太还理解的,博主也是想了半天才理解了.

优化后的代码:

class Solution {
public:
   int numDecodings(string s) {
  			int n=s.size();
            vector<int> dp(n+1);
            dp[0]=1;
            dp[1]=s[1-1]!='0';//方便理解下标对应
            for(int i=2;i<=n;i++)
            {
                if(s[i-1]!='0')dp[i]+=dp[i-1];
                int t=(s[i-2]-'0')*10+s[i-1]-'0';
                if(t>=10&&t<=26)dp[i]+=dp[i-2];
            }
            return dp[n];
    }
};