原论文:From ranknet to lambdarank to lambdamart: An overview
构造样本&损失函数
首先对同一个query下返回的连接,进行配对构造样本<Ui, Uj>代表了一对样本。用Pij代表样本的得分,si,sj代表了模型对样本的打分。
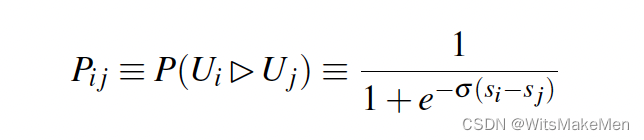
有了样本模型打分后,需要构造样本的真实得分。其中Sij代表了Ui,Uj用户评估的好坏程度,可以用用户行为表示,比如说用户点击了Ui,而没有点击Uj,则Sij = 1,反之Sij=-1,如果都没有点击或者都点击了则Sij=0。
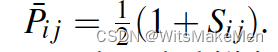
有了真实得分和模型打分后,我们来构造损失函数,就是如下的交叉熵损失函数。
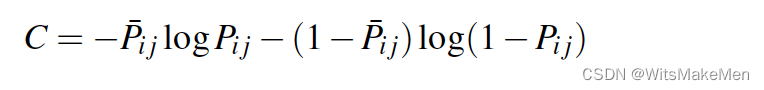
求梯度
首先将Pij带入到C中,可以简化后得到如下公式:
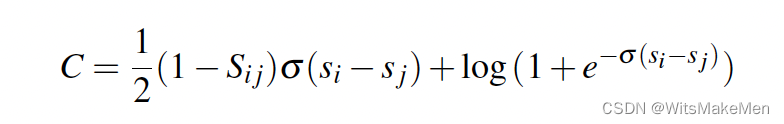
对于Sij=1和Sij=-1的情况,我们可以得到一个对称的C
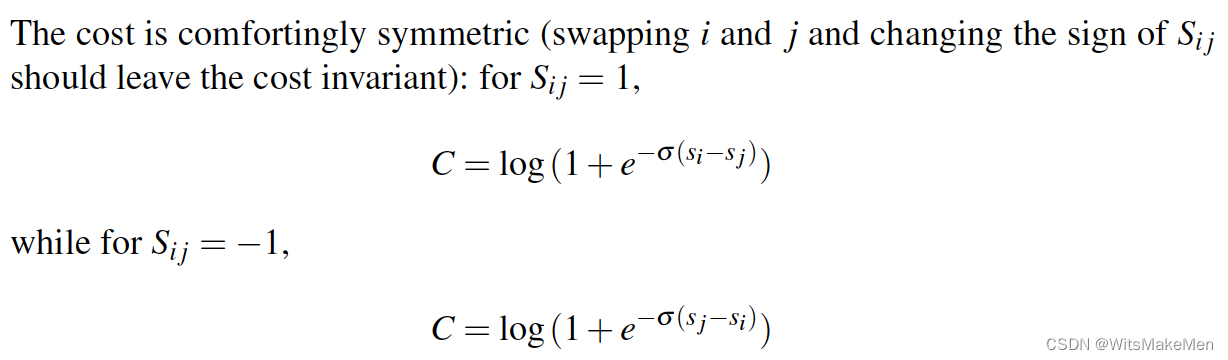
利用求导法则,我们发现C对si和sj求导,是对称的。
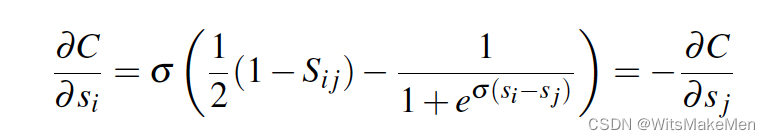
如果我们想求对于Wk的导数的话,可以通过如下链式法则得到。并且计算Wk的梯度。
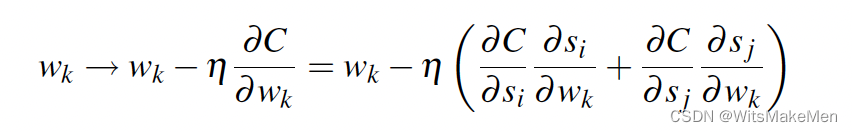
加速优化
有了以上的梯度后,对于每一个Wk都要求这样一对导数,计算效率可以进一步提升,因为C对si,sj的导数是负数对称关系,所以可以得到如下一个简化。
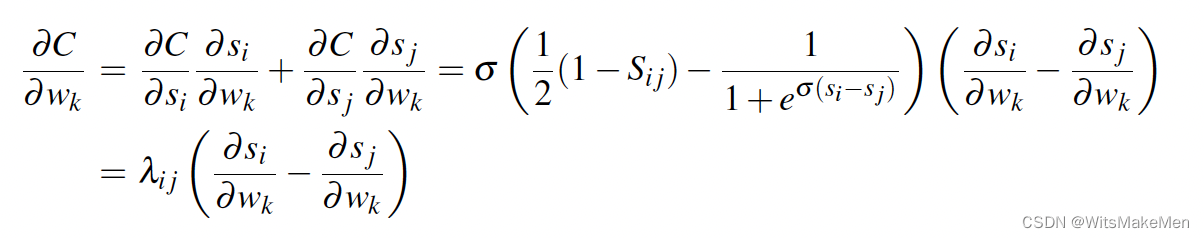
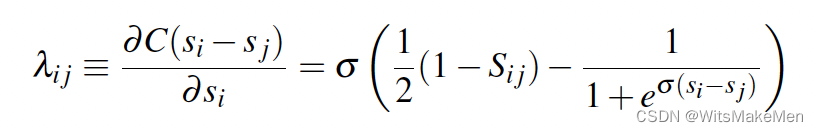
进一步的我们让所有的si对应的pair对进行分组,然后会得到如下简化。这样由于可以从模型打分中,提前算好所有的C对s的梯度,所以,可以避免很多的重复计算,大大提升了速度。
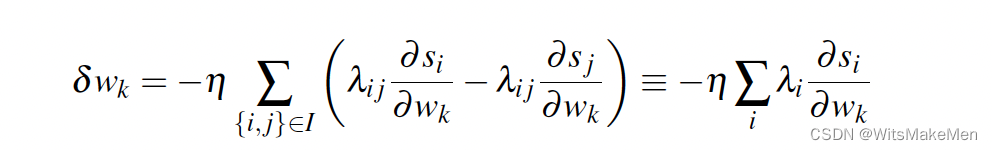
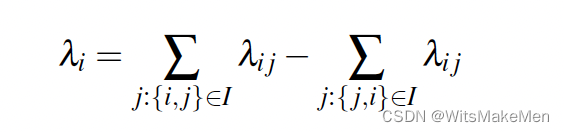
到这里就完成了Pairwise的模型打分到梯度计算的转化。