❤️博客主页： 小镇敲码人
🍏 欢迎关注：👍点赞 👂🏽留言 😍收藏
🌞友友们暑假快乐，好久不见呀！！！💖💖💖
🍉 有人曾经问过我这样一个问题，“人终其一身，执着追求的东西究竟是什么？”我是这样回答的，”我们终其一生都在寻找着那个和我们灵魂极其契合的人，可最后才发现，那个人只有也只能是自己，学会在无聊时消遣自己是非常重要的“，所以无论目前屏幕上的你深处怎样的绝境之中，请不要放弃自己，好好的爱自己就是度过绝境的最佳武器！！！😸😸😸

一、时间复杂度

1.1时间复杂度的定义

         在计算机与科学中，算法的时间复杂度（time complexity）是一个函数，它定性的描述算法的运行时间，表示一个程序来回执行的次数，但不定量。这个函数的自变量是算法输入值的字符串的长度，即$N$。时间复杂度常用大O符号表述，只包括那个幂次最高的项数。使用这种方式时，时间复杂度可被称为是渐近的，也就是 $\underset{N\to \infty }{\lim }O(N)$时的情况。例如，如果一个算法对于任何大小为 $N$的输入，它至多需要 5$N^3$ + $3N$ 的时间运行完毕，那么它的渐近时间复杂度是 $O(N^3)$。

• 注意：时间复杂度不计算时间，只计算程序的执行次数。

常见的时间复杂度包括：

• 常数时间复杂度（$O(1))$：算法的执行时间与输入规模无关，常数级别的执行时间。
• 线性时间复杂度（$O(N)$）：算法的执行时间与输入规模线性相关，随着输入规模的增加而线性增长。
• 对数时间复杂度（$O(logN)$）：算法的执行时间与输入规模的对数关系，通常是二分查找等算法的时间复杂度。
• 平方时间复杂度（$O(N^2)$）：算法的执行时间与输入规模的平方相关，通常是嵌套循环等算法的时间复杂度。
• 线性对数时间复杂度$(O(N\ast logN))$ ：它表示随着输入规模 N 的增加，算法的执行时间以 N 乘以 log N 的速度增长,线性对数时间复杂度常常出现在一些高效的排序算法（如快速排序和归并排序）以及一些分治算法中。

注意：嵌套循环的算法时间复杂度不一定是$O(N^2)$。

通过分析算法的时间复杂度，我们可以更好地理解算法的性能特点，并进行算法的选择和优化。

1.2 常见的时间复杂度的计算

1.2.1 常数时间复杂度（$O(1))$

    int main()
    {
      int a = 0;
      a += 1;
      printf("%d",&a);
      return 0;
    }

这段代码执行了四次操作。我们逐行分析代码的执行过程：

1.int a = 0;：这行代码初始化了整数变量a，将其赋值为 0。
2. a += 1;：这行代码将变量 a的值增加 1，现在 a 的值为 1。
3.printf("%d", &a);：这行代码使用 printf 函数打印变量 a 的值的内存地址，格式化输出为十进制整数。
4. return 0;：在 main 函数的结尾，使用 return 语句将返回值设为 0。
因此，代码执行了四次操作。

• 若对于一个算法$T(n)$的上界与输入大小无关，则称其具有常数时间，记作O(1)时间,故而这个算法的时间复杂度为$O(1)$。

1.2.2 线性时间复杂度（$O(N)$）

int main()
{
  int n = 0;
  scanf("%d",&n);
  int sum = 1;
  for(int i = 1;i < n;;i++)
    sum *= i;
  printf("%d",sum);
  return 0;
}

这段代码的执行过程如下：

1. int n = 0;：这行代码声明了一个整数变量 n，并将其初始化为 0。
2. scanf("%d",&n);：这行代码使用 scanf 函数从标准输入中读取一个整数，并将其赋值给变量 n。
3. int sum = 1;：这行代码声明了一个整数变量 sum，并将其初始化为 1。
4. for(int i = 1;i < n;i++)：这行代码开始一个 for 循环，循环变量 i 的初始值为 1，循环条件为 i < n。
5. sum *= i;：这行代码将变量 sum 与变量 i 相乘，并将结果赋值给 sum。
6. printf("%d",sum);：这行代码使用 printf 函数打印变量 sum 的值。
7. return 0;：在 main 函数的结尾，使用 return 语句将返回值设为 0。
8. 在for循环中，变量 i 的初始值为 1，每次循环 i 的值递增 1，直到达到 n 的值。因此，for 循环的执行次数为 n - 1。在循环中，执行了一次乘法操作 sum *= i，共执行了 n - 1 次。

• 故而程序的执行次数为：$T（N）=5+2\ast (N-1)=2N+3,$$\underset{N\to \infty }{\lim }T(N)=O(N)$。

1.2.3 对数时间复杂度（$O(logN)$）

#include <stdio.h>

void logarithmicAlgorithm(int n) {
    int i = 1;
    while (i < n) {
        printf("%d\n", i);
        i *= 2;  // 对数时间复杂度的关键步骤
    }
}

int main() {
    int n = 16;
    logarithmicAlgorithm(n);
    return 0;
}

这段代码的执行过程如下：

1. 在 main函数中，声明一个整数变量 n 并赋值为 16。
2. 调用logarithmicAlgorithm()函数，并将变量 n 作为参数传递给该函数。
3. 进入logarithmicAlgorithm函数。
4. 在logarithmicAlgorithm 函数中，声明一个整数变量 i 并赋值为 1。
5. 进入 while 循环，检查条件 i < n 是否满足。由于此时 i 的初始值为 1，且 1 小于 16，条件成立，进入循环体。
6. 在循环体内，使用printf 函数打印变量 i 的值。
7. 执行i *= 2，将 i 的值乘以 2。
8. 回到循环的开头，再次检查条件 i < n。如果条件仍然成立，继续执行循环体；如果条件不成立，跳出循环。
9. 当 i 的值达到或超过 n（即 16）时，条件 i < n 不再满足，跳出循环。
10. 退出logarithmicAlgorithm函数。
11. 回到 main函数，继续执行后续的代码。执行return 0; 语句，结束程序。

• 设while循环的判断执行次数为x，$2=N,\Rightarrow 2^{x-1}=lo{g}_{2}N+1$
  while循环内的执行次数为$2\ast lo{g}_{2}N$

• 故而程序的执行次数为：$T（N）=7+3\ast lo{g}_{2}N,$$\underset{N\to \infty }{\lim }T(N)=O(logN)$。

1.2.4 平方时间复杂度（$O(N^2)$

#include <stdio.h>

void quadraticAlgorithm(int n) {
    for (int i = 1; i <= n; i++) {
        for (int j = 1; j <= n; j++) {
            printf("(%d, %d)\n", i, j);
        }
    }
}

int main() {
    int n = 3;
    quadraticAlgorithm(n);
    return 0;
}

这段代码的执行过程如下：

1. 在main函数中声明一个整数变量n，并赋值为3。
2. 调用quadraticAlgorithm()函数，并把变量n作为形参传递给函数。
3. 进入函数quadraticAlgorithm()。
4. 外部for循环的判断执行次数为n+1，外部循环循环一次内部for循环判断的执行次数为n+1，printf语句的执行次数为n。

故而外部for循环的执行次数就为n+1，内部for循环的总执行次数就为n*（n+1），内部for循环的printf语句的总执行次数为$n^2$

5. 退出函数quadraticAlgorithm()。
6. 继续执行main函数中的return 0;语句，结束程序。

• 故程序的执行次数为：$T(N)=1+1+1+(N+1)+N\ast (N+1)+N\ast N+1+1=2N^2+2N+6,$$\underset{N\to \infty }{\lim }T(N)=O(N^2)$

1.3 常见的函数的时间复杂度

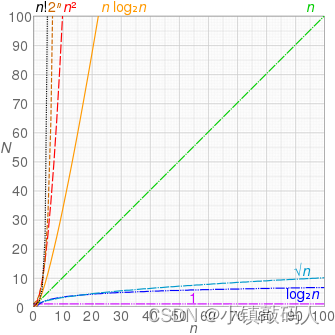
以下图片整理了一些常用的时间复杂度类。表中，$poly(x)=xO(1)$，也就是 x 的多项式。也可以访问网页版点击此处跳转

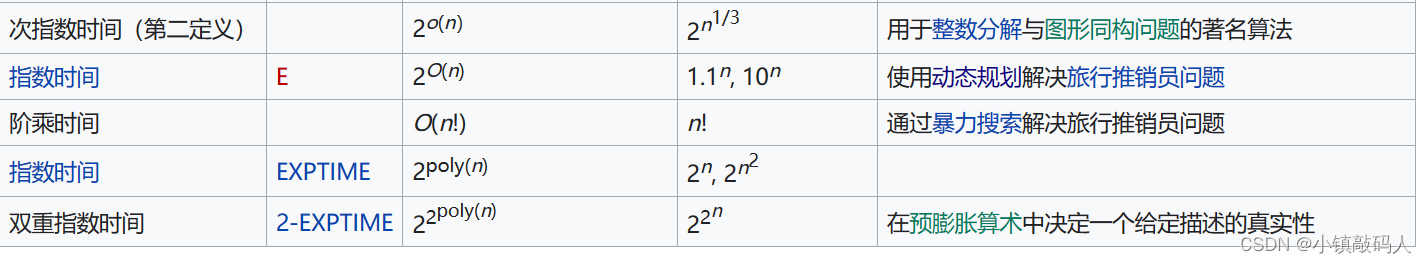
二、空间复杂度

2.1 空间复杂度的定义

      在计算机科学中，一个算法或程序的空间复杂度定性地描述该算法或程序运行所需要的存储空间大小。空间复杂度是相应计算问题的输入值的长度的函数，它表示一个算法完全执行所需要的存储空间大小。和时间复杂度类似，空间复杂度通常也使用大O记号来渐进地表示。例如：$O(n)、O(n^{\alpha })、O(n\ast logn)、O(2^n)$。
      空间复杂度用于评估算法在执行过程中所需的额外空间或内存的量级或增长趋势。它主要关注算法在运行过程中所使用的额外存储空间，包括算法使用的数据结构、临时变量、递归调用等。

• 注意：空间复杂度不计算空间，只计算变量的个数

常见的空间复杂度包括：

• 常数空间复杂度$(O(1))$：算法使用固定的额外空间，不随输入的增加而变化。
• 线性空间复杂度$(O(n))$：算法使用的额外空间与输入规模成线性关系。
• 平方空间复杂度$(O(n^2))$：算法使用的额外空间与输入规模成平方关系。
• 对数空间复杂度$(O(logn))$：算法使用的额外空间与输入规模成对数关系。

2.2 常见的空间复杂度的计算

• 就是去算变量和函数调用开辟的栈帧的个数之和

2.2.1 常数空间复杂度$(O(1))$

void printHello() {
    printf("Hello, world!\n");
}

• 函数调用一次，开辟一个栈帧，空间复杂度为$O(1)$。

2.2.2 线性空间复杂度$(O(n))$

void printNumbers(int n) {
    int *arr =(int*)malloc(n * sizeof(int));
    // 执行其他操作...
    free(arr);
}

• 开辟了一个动态数组，变量的个数与$n$成正比，取极限，和时间复杂度一样，常数可以忽略，空间复杂度为$O(n)$。

2.2.3 平方空间复杂度$(O(n^2))$

void printPairs(int n) {
    int **matrix = (int**)malloc(n * sizeof(int *));
    for (int i = 0; i < n; i++) {
        matrix[i] = (int*)malloc(n * sizeof(int));
    }
    // 执行其他操作...
    for (int i = 0; i < n; i++) {
        free(matrix[i]);
    }
    free(matrix);
}

• 开辟了一个二维的动态数组，变量的个数与$n^2$成正比，取极限，忽略常数，空间复杂度为$O(n^2)$。

2.2.4 对数空间复杂度$(O(logn))$

// 递归二分查找函数
int binarySearch(int arr[], int low, int high, int target) {
    if (low <= high) {
        int mid = low + (high - low) / 2;

        if (arr[mid] == target) {
            return mid;
        } else if (arr[mid] < target) {
            return binarySearch(arr, mid + 1, high, target);
        } else {
            return binarySearch(arr, low, mid - 1, target);
        }
    }
    return -1; // 如果找不到目标元素，返回-1
}

    数组是提前排好序的递增数组，假设同时存在的栈帧最多为x个,因为只有找不到或者找到了target函数才会返回，此时区间长度要么是1，要么没找到不构成区间了，函数调用产生的栈帧才会开始销毁，有$2^x=n\to x=lo{g}_{2}n$,也就是最多开辟了$lo{g}_{2}n$个栈帧。

• 故取极限,空间复杂度$T(N)为$$$\underset{N\to \infty }{\lim }T(N)=O(logN)$。