常微分方程(ODE)求解方法总结(续)
- 1 隐式方法
- 2 多步法
- 2.1 二阶方法
- 2.1.1 非自启动修恩方法
- 2.2 开型和闭型积分公式
- 2.3 高阶多步法
1 隐式方法
常微分方程(ODE)求解方法总结 里面介绍了我称为“正常思路”的方法,就是 y i + 1 = y i − a y i ∗ h y_{i+1}=y_i - ay_{i}*h yi+1=yi−ayi∗h,从 y i y_i yi推出 y i + 1 y_{i+1} yi+1这种思路。这种思路的方法称之为显式方法,也可以称为前向方法。// (原来形式为 y i + 1 = y i + f ( x i , y i ) ∗ h y_{i+1}=y_i+ f(x_i, y_i)*h yi+1=yi+f(xi,yi)∗h,为了与下面的隐式对比方便,写成 y i + 1 = y i − a y i ∗ h y_{i+1}=y_i - ay_{i}*h yi+1=yi−ayi∗h)。
还有另外一种思路,就是,
y
i
+
1
=
y
i
−
a
y
i
+
1
∗
h
y_{i+1}=y_i - ay_{i+1}*h
yi+1=yi−ayi+1∗h这种思路,由此式可以得出:
y
i
+
1
=
y
i
/
(
1
+
a
)
h
y_{i+1}=y_i /(1+a)h
yi+1=yi/(1+a)h (1.1)
这种思路方法称为隐式方法,或者后向方法。
这种方法有很多应用,因为其有一个优点就是,这种方法不会因为步长选取不当而出现不稳定的问题,因此,该方法称作无条件稳定。( 这个先不说具体原因,后面会讲到。)
这种方法的特点就是,将
y
i
+
1
y_{i+1}
yi+1先作为已知的点,来参与计算。
2 多步法
前一篇文章和这一篇文章的上一章节里面主要都是讲了单步法,就是从 y i y_i yi推出 y i + 1 y_{i+1} yi+1,过程中只需要一个知道前一个点 y i y_i yi。
常微分方程(ODE)求解方法总结 里面“第2.1.5 欧拉方法的改进思路3”里面有讲到,能不能用取三个点、四个点等用二次曲线和三次曲线来插值逼近使积分结果更加接近真实值。
接下来,就会沿着这个思路前进。
2.1 二阶方法
在讨论高阶形式之前,先给出一个简单的二阶方法,便于理解。
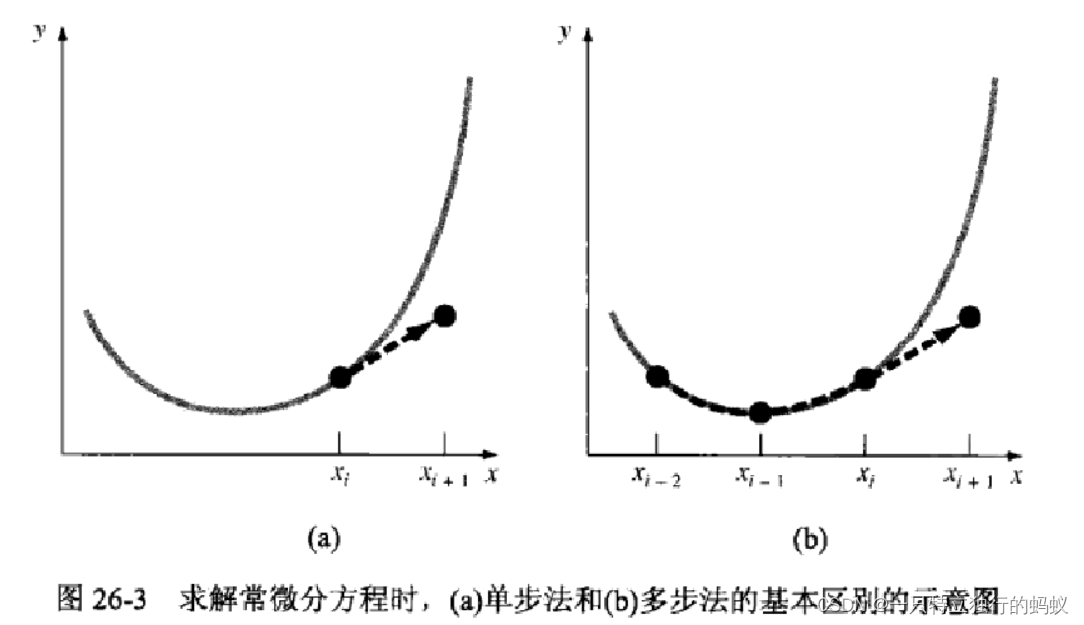
单步法是通过
x
i
x_i
xi点的值估计
x
i
+
1
x_{i+1}
xi+1处的值。二阶方法,就是用
x
i
−
2
x_{i-2}
xi−2、
x
i
−
1
x_{i-1}
xi−1、
x
i
x_{i}
xi点的值通过二次插值来估计
x
i
+
1
x_{i+1}
xi+1处的值。
2.1.1 非自启动修恩方法
2.2 开型和闭型积分公式
2.3 高阶多步法
(未完待续。。。)