反向传播算法对于快速训练大型神经网络至关重要。本文将介绍算法的工作原理。

目录

1.简单的神经网络

2.激活函数

3.错误函数

4.正向传播

4.1 更新隐藏层

5.反向传播

5.1 求导数

5.2 其他导数

5.3 反向传播误差倒数

6.参考文献

---

1.简单的神经网络

如图 1 所示，展示了一个神经网络，其中包含一个输入节点、一个输出节点以及两个隐藏层（分别有两个节点）。相邻层中的节点使用权重 （网络参数）连接。

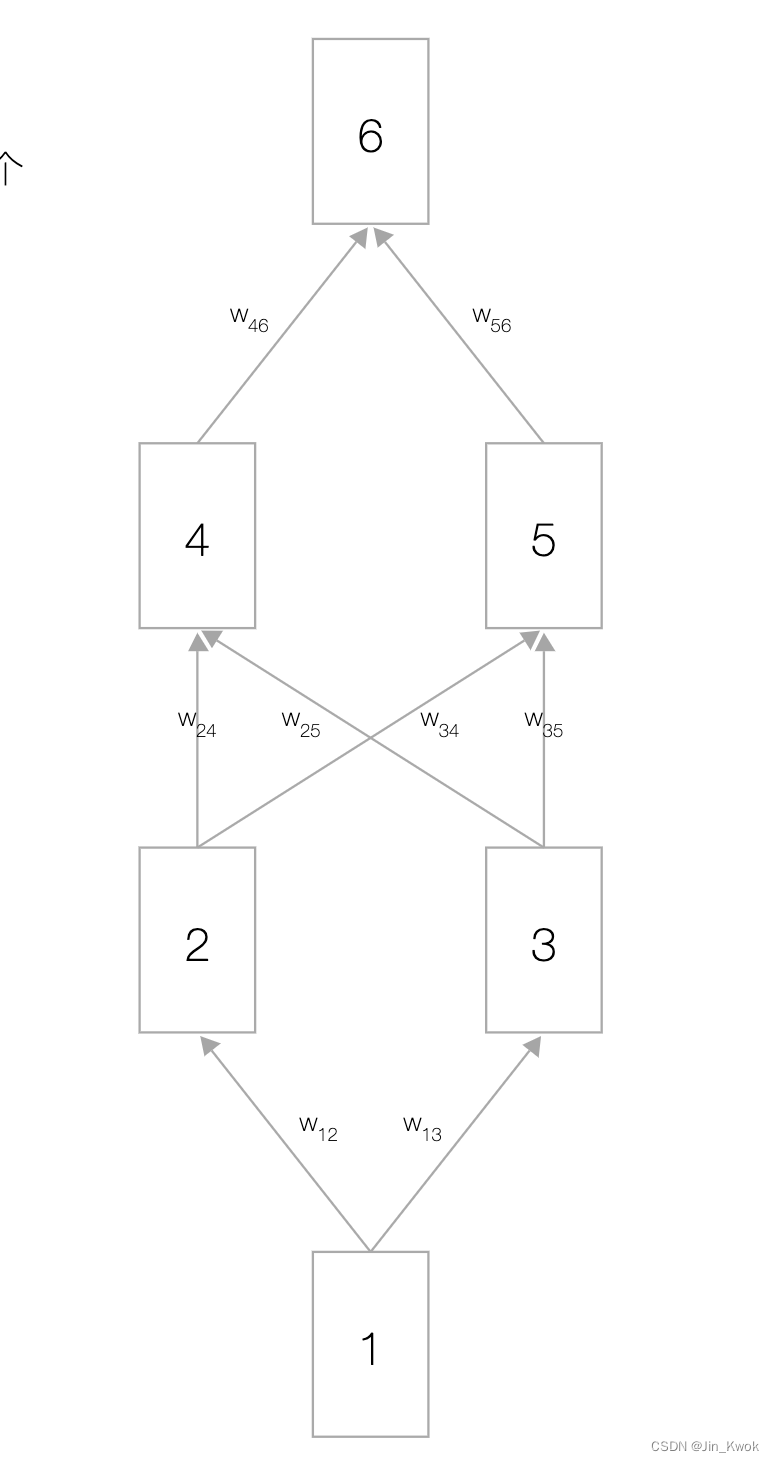
图 1 神经网络示意图

2.激活函数

如图 2 所示，每个节点都有一个总输入 、一个激活函数  和一个输出 。   必须是非线性函数，否则神经网络将只能学习线性模型（相关内容在【机器学习15】一文中有介绍）。常用的激活函数是 S 型函数： 

图 2 神经网络节点内部示意图

3.错误函数

错误函数的作用在于自动从数据中学习网络的权重，以使预测的输出  接近所有输入的目标  。 为了衡量目标的完成程度，我们使用误差函数 𝐸。 常用的错误函数是 ：

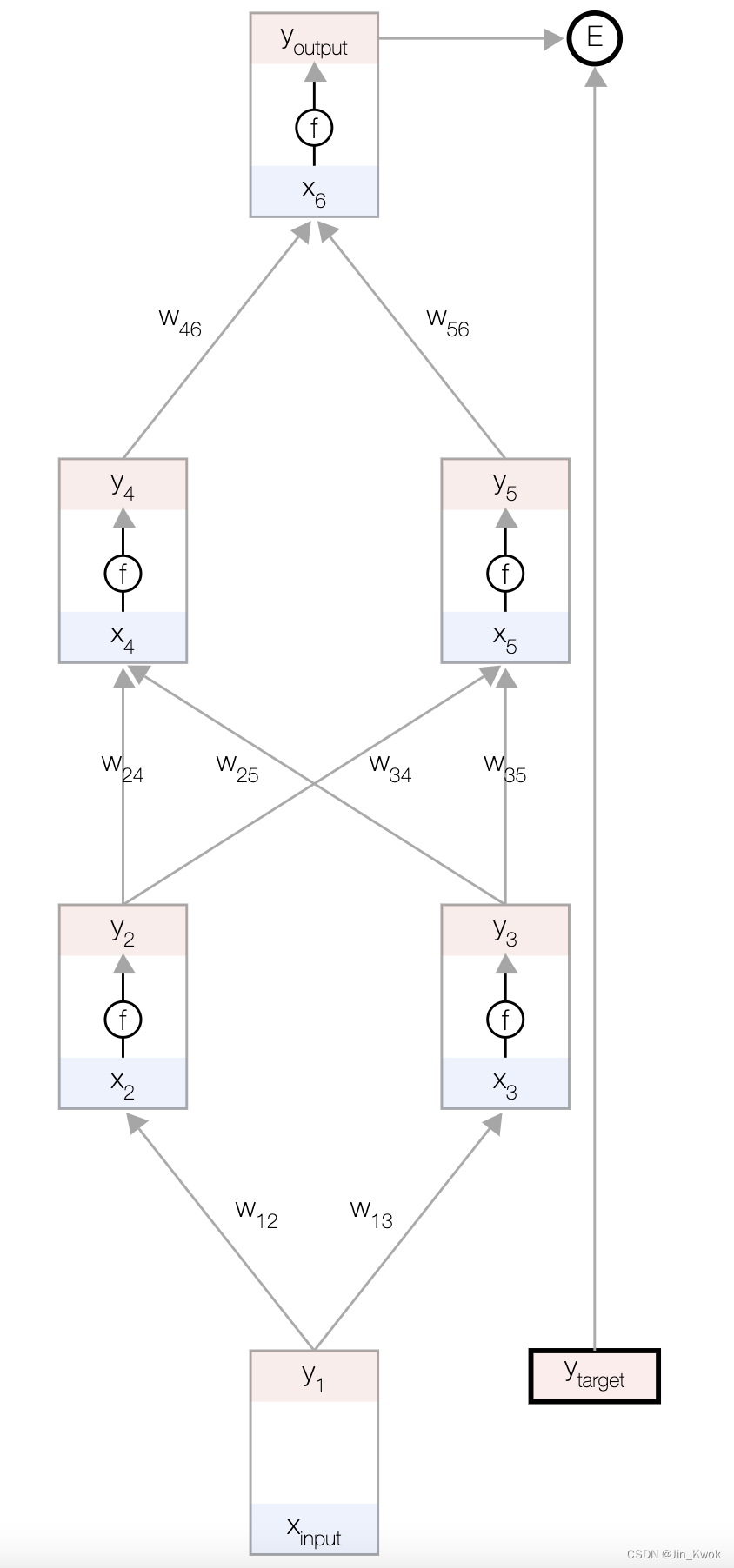
图 3 错误函数示意图

4.正向传播

如图 4 所示，以输入示例  为例，并更新网络的输入层。为保持一致，我们认为输入与任何其他节点类似，由于输入层没有激活函数，因此其输出等于其输入，即 。

图 4 正向传播

4.1 更新隐藏层

如图 5 所示，我们更新第一个隐藏层。我们会获取上一层中节点的输出 y ，并使用权重来计算下一层中节点的输入 𝑥。

图 5 更新隐藏层

然后，如图 6 所示，我们更新第一个隐藏层中节点的输出。 为此，我们使用激活函数 𝑓(𝑥)。

𝑦=𝑓(𝑥)

图 6 更新隐藏层输出

 根据上面的计算方法，我们针对网络的剩余部分进行传播，并获取网络的最终输出。

图 7 继续传播，直到获得最终输出

5.反向传播

5.1 求导数

5.2 其他导数

5.3 反向传播误差倒数

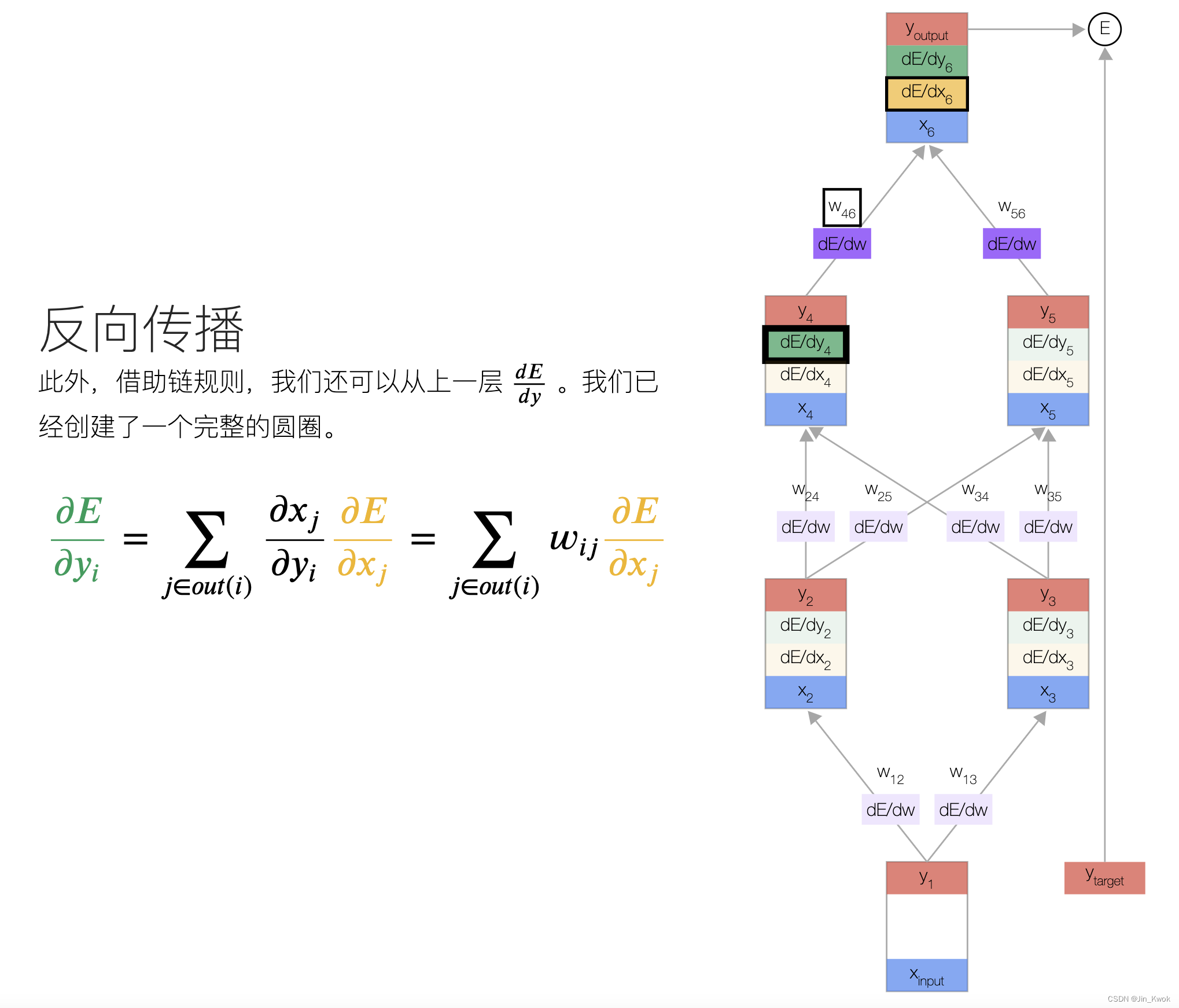
重复上面的步骤和三个公式，继续传播，直到我们计算完所有误差导数为止。

6.参考文献

Google for Developers：https://google-developers.gonglchuangl.net/machine-learning/crash-course/backprop-scroll?hl=zh-cn