【动态规划算法】第三题：746.使用最小花费爬楼梯

news2024/11/26 4:47:55

💖作者：小树苗渴望变成参天大树
🎉作者宣言：认真写好每一篇博客
🎊作者gitee:gitee
💞作者专栏：C语言,数据结构初阶,Linux,C++ 动态规划算法

如果你喜欢作者的文章，就给作者点点关注吧！

文章目录

前言

前言

今天我们开始讲解动态规划的第三题，难度上有一点小提升，不太很好理解，这题目有两种解题办法，博主都会使用动态规划的五个步骤给大家进行讲解，我们来看下面的正文

第二个题目是使用最小花费爬楼梯
在这里插入图片描述

解法一：（以i为到达点，通过前面的费用来推后面的）
图解：
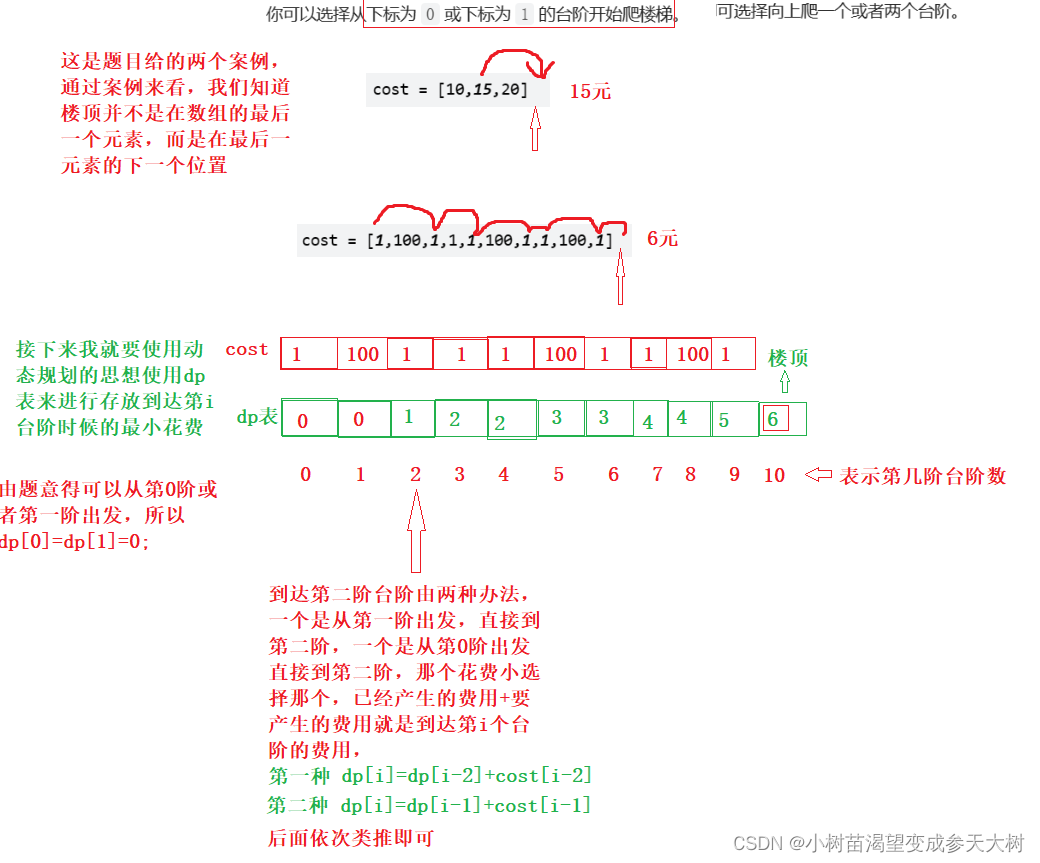
在这里插入图片描述
通过动态规划的五个步骤解题：

状态表示：创建一个dp表，根据经验以i位置为到达点，即到达第i个台阶需要花费的最小费用为dp[i]（注意：i位置的费用不用计算，只有往上走才需要算）。 根据图解，就是当i=2时，到达第二阶台阶所花费的最小费用为dp[i]
状态转移方程：以离此状态最近的状态来研究两者的关系。到达第i的位置时，最近时先到达i-1的位置或者到达i-2的位置，来算算两者谁到达i位置的费用最低，通过状态表示，dp[i]表示到达i位置的最小费用，
（1）那么从i-1的位置到达i位置的最小费用为dp[i-1]+往上爬一步所需的费用为cost[i-1]。 dp[i]=dp[i-1]+cost[i-1]
（2）同理，那么从i-2的位置到达i位置的最小费用为dp[i-2]+往上爬两步所需的费用为cost[i-2]。 dp[i]=dp[i-2]+cost[i-2]
所以状态转移方程为两者最小的：dp[i]=min(dp[i-1]+cost[i-1],dp[i]=dp[i-2]+cost[i-2])
初始化：保证数组不越界，出现i-1和i-2，所以dp[0],dp[1]要初始化从dp[2]开始算，根据题目要求，到达第0阶或者到达第1阶不需要费用，所以dp[0]=dp[1]=0;
填表顺序：从左往右
返回值，根据题目要求和状态表示，dp[n]就是到达第n阶台阶的最小费用

代码实现：

class Solution {
public:
    int minCostClimbingStairs(vector<int>& cost) {
        int n=cost.size();//计算cost数组的大小
        //1.创建dp表
        vector<int> dp(n+1);//vector默认给数组的初始化就是0
        for(int i=2;i<=n;i++)
        {
           dp[i]=min(dp[i-1]+cost[i-1],dp[i-2]+cost[i-2]);
           
        }
        return dp[n];//返回值

    }
};

解法二：（以i位置为出发点，到达楼顶的最小费用，通过后面来推前面）
图解
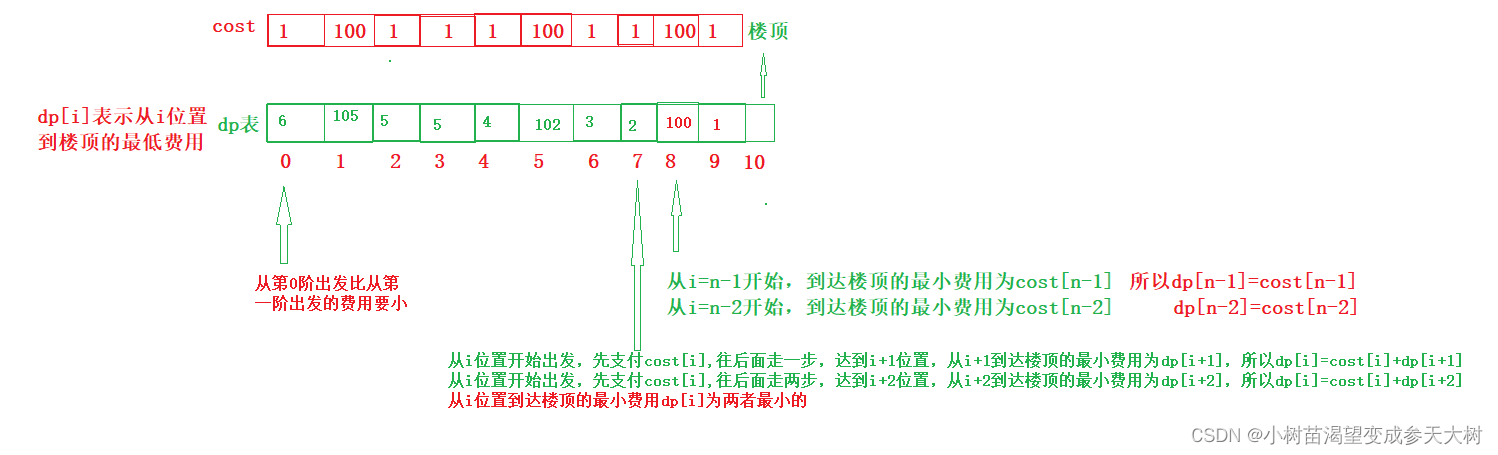
在这里插入图片描述
通过动态规划的五个步骤解题：

状态表示：根据解法一，创建一个dp表，以i位置为出发点，dp[i]表示：从i位置到达楼顶的最小费用。因为从n-1h和n-2位置开始到楼顶的最小费用是直接可以得出来的，第n个位置的费用就可以不用计算了，所以dp表的大小和原数组大小一样即可
状态转移方程：通过状态表示第i位置到达了，楼顶的最小费用为dp[i],从i位置出发，想要到达楼顶，右两种方式
（1）先支付cost[i],往后面走一步，到达i+1的位置，i+1到达楼顶的最小费用是知道的为dp[i+1],所以从i位置到达楼顶的费用为dp[i]=dp[i+1]+cost[i]
（2）同理，先支付cost[i],往后面走两步，到达i+2的位置，i+2到达楼顶的最小费用是知道的为dp[i+2],所以从i位置到达楼顶的费用为dp[i]=dp[i+2]+cost[i]

所以从i位置到达楼顶的最小费用为dp[i]=min(dp[i+1]+cost[i],dp[i+2]+cost[i])
3. 初始化：保证数组不越界,可以楼顶到前一步或者前两部达到楼顶的最低费用为dp[n-1]=cost[n-1],dp[n-2]=cost[n-2]
4. 填表顺序：从右往左
5. 返回值：我们是从后面往前面推，一开始出发右两种方式，就是从0阶或者1阶出发，比较两者谁的费用最小即可，即返回min(dp[0],dp[1]);

代码实现：

class Solution {
public:
    int minCostClimbingStairs(vector<int>& cost) {
        int n=cost.size();//计算cost数组的大小
        //1.创建dp表
        vector<int> dp(n);//vector默认给数组的初始化就是0
        if(n==0||n==1)return 0;
        dp[n-1]=cost[n-1];//初始化
        dp[n-2]=cost[n-2];
        for(int i=n-3;i>=0;i--)
            dp[i]=min(dp[i+1]+cost[i],dp[i+2]+cost[i]);//状态转移方程

        return min(dp[0],dp[1]);//返回值
    }
};